A bead can slide on a smooth circular wire frame of radius R which is fixed in a vartical plane. The bead is displaced slightly from the highest point of the wire frame. The speed of the bead subsequently as a function of the angle θ made by the bead with the vertical line is
√2gR
√2gR(1−sinθ)
√2gR(1−cosθ)
2√gR
The correct Answer is:C
To find the speed of the bead as a function of the angle θ made with the vertical line, we can use the principle of conservation of mechanical energy. Here are the steps to derive the speed:
Step 1: Understand the Initial and Final States
- Initially, the bead is at the highest point of the circular wire frame (point A) and is at rest. Therefore, its initial kinetic energy (KE) is 0, and its potential energy (PE) is maximum.
- When the bead is displaced to an angle θ (point B), it has some speed (v) and a lower potential energy.
Step 2: Define the Height Change
- The height (h) of the bead when it is at angle θ can be calculated as:
h=R−Rcosθ=R(1−cosθ)
Here, R is the radius of the circular wire frame.
Step 3: Write the Conservation of Energy Equation
- According to the conservation of energy:
Total Energy at A=Total Energy at B
KEA+PEA=KEB+PEB
- At point A (highest point):
- KEA=0
- PEA=mgR (taking the reference point at B)
- At point B (displaced point):
- KEB=12mv2
- PEB=0 (taking the potential energy at point B as zero)
Step 4: Set Up the Equation
- Plugging in the values:
0+mgR=12mv2+0
- This simplifies to:
mgR=12mv2
Step 5: Cancel Mass and Rearrange
- Cancel the mass (m) from both sides (assuming m ≠ 0):
gR=12v2
- Rearranging gives:
v2=2gR
Step 6: Substitute for Height
- Now, substituting the height (h) we found earlier:
v2=2g(R(1−cosθ))
- Therefore, we have:
v=√2gR(1−cosθ)
Final Result
The speed of the bead as a function of the angle θ is:
v=√2gR(1−cosθ)
- Initially, the bead is at the highest point of the circular wire frame (point A) and is at rest. Therefore, its initial kinetic energy (KE) is 0, and its potential energy (PE) is maximum.
- When the bead is displaced to an angle θ (point B), it has some speed (v) and a lower potential energy.
- The height (h) of the bead when it is at angle θ can be calculated as:
h=R−Rcosθ=R(1−cosθ)
Here, R is the radius of the circular wire frame.
- According to the conservation of energy:
Total Energy at A=Total Energy at B
KEA+PEA=KEB+PEB
- At point A (highest point):
- KEA=0
- PEA=mgR (taking the reference point at B)
- At point B (displaced point):
- KEB=12mv2
- PEB=0 (taking the potential energy at point B as zero)
- Plugging in the values:
0+mgR=12mv2+0
- This simplifies to:
mgR=12mv2
- Cancel the mass (m) from both sides (assuming m ≠ 0):
gR=12v2
- Rearranging gives:
v2=2gR
- Now, substituting the height (h) we found earlier:
v2=2g(R(1−cosθ))
- Therefore, we have:
v=√2gR(1−cosθ)
The speed of the bead as a function of the angle θ is:
v=√2gR(1−cosθ)
Topper's Solved these Questions
- WORK, POWER, AND ENERGYBOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - PRACTICE QUESTIONS (More than one choice correct type)
10 Videos
- WORK, POWER, AND ENERGYBOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - PRACTICE QUESTIONS (Linked Comprehension)
9 Videos
- WORK, POWER, AND ENERGYBOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - PROBLEMS
58 Videos
- WAVES-IBOOK - RESNICK AND HALLIDAYCHAPTER - WAVES-IEXERCISE - Practice Questions (Integer Type)
4 Videos
Similar Questions
A small 100g sleeve B can slide on a smooth, circular and rigid wire frame A of radius 5m placéd in vertical plane. The wire frame is rotating about its vertical diameter at 2rads. When the sleeve is brought at a particular angular position other than the bottom and the top of the ring, the sleeve will not slide on the wire frame. What is force of interaction (in N) between the sleeve and the wire frame at this position?
'(##CEN_KSR_PHY_JEE_C07_020_Q11##)'
View SolutionA circular wire frame of radius R is rotating about its fixed vertical diameter. A bead on the wire remains at rest relative to the wire at a position in which the radius makes an angle θ with the vertical (see figure). There is no friction between the bead and the wire frame. Prove that the bead will perform SHM (in the reference frame of the wire) if it is displaced a little from its equilibrium position. Calculate the time period of oscillation.
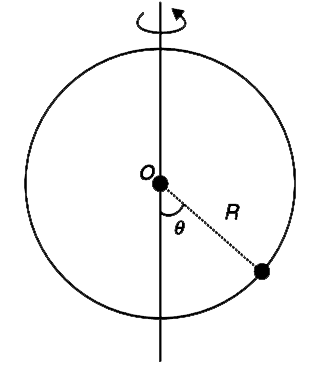
View Solution
Knowledge Check
A bead can slide on a smooth circular wire frame of radius r which is fixed in a vertical plane. The bead is displaced slighty from the highest point of the wire frame. The speed of the bead subsequently as a function of the angle θ made by the bead with the verticle line is
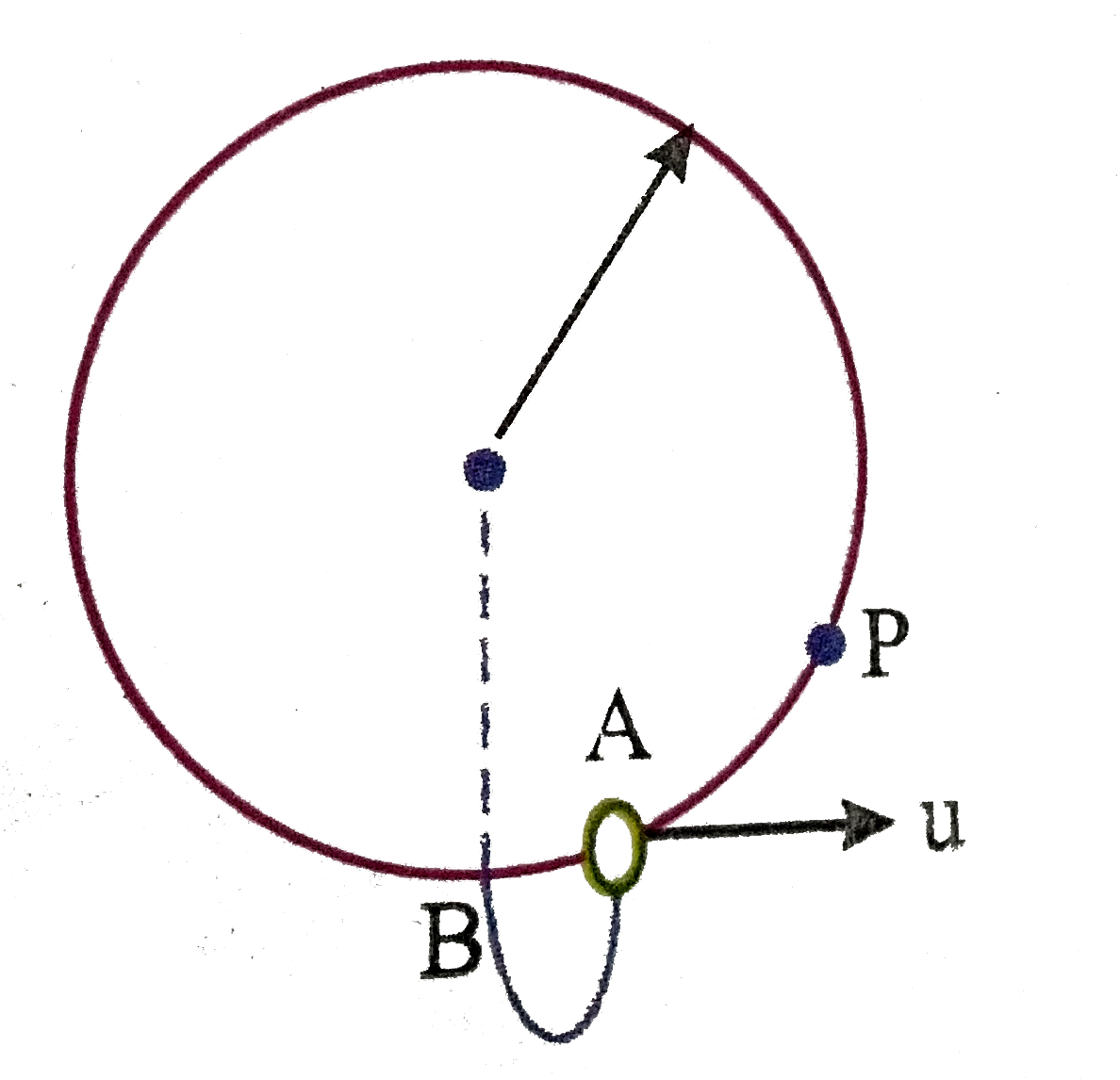
A√2grB√2gr(1−sinθ)C√2gr(1−cosθ)D2√grA bead of mass m is threaded on a smooth circular wire centre O, radius a, which is fixed in vertical plane. A light string of natural olength 'a', elastic constant =3mga and breaking strength 3mg connects the bead to the lowest point A of the wire. The other end of the string is fixed to ring at point B near point A. The string is slaked initially. The bead is projected from A with speed u.

If v=2u0, the tension T in th elastic string when the bead is at the highest point B of the wire isA3μ20aB4mgC2mgD(4u20a−g)mA bead of mass m is threaded on a smooth circular wire centre O, radius a, which is fixed in vertical plane. A light string of natural olength 'a', elastic constant =3mga and breaking strength 3mg connects the bead to the lowest point A of the wire. The other end of the string is fixed to ring at point B near point A. The string is slaked initially. The bead is projected from A with speed u.
The elastic energy stored in the string when the bead is at the highest point B will beA3mga2B2mgaC4mgaD2mga2
A bead of mass m is threaded on a smooth circular wire centre O, radius a, which is fixed in vertical plane. A light string of natural olength 'a', elastic constant =3mga and breaking strength 3mg connects the bead to the lowest point A of the wire. The other end of the string is fixed to ring at point B near point A. The string is slaked initially. The bead is projected from A with speed u.
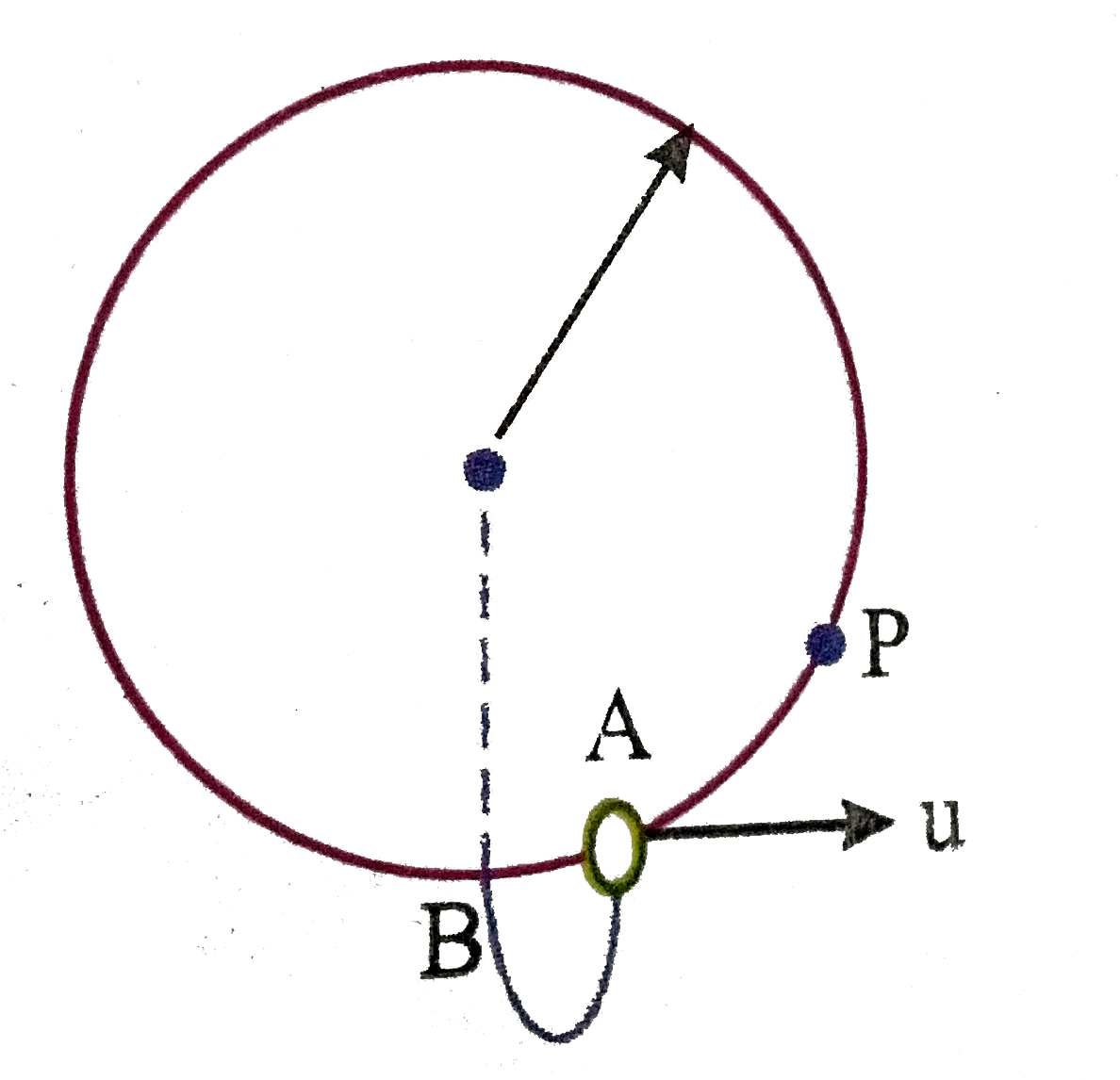
The smallest value u0 of u for which the bead will make complete revolutions of the wire will be
View SolutionA bead is free to slide down a smooth wire tightly stretched between points A and B on a vertical circle. If the starts from rest at A, the heighest point on the circle
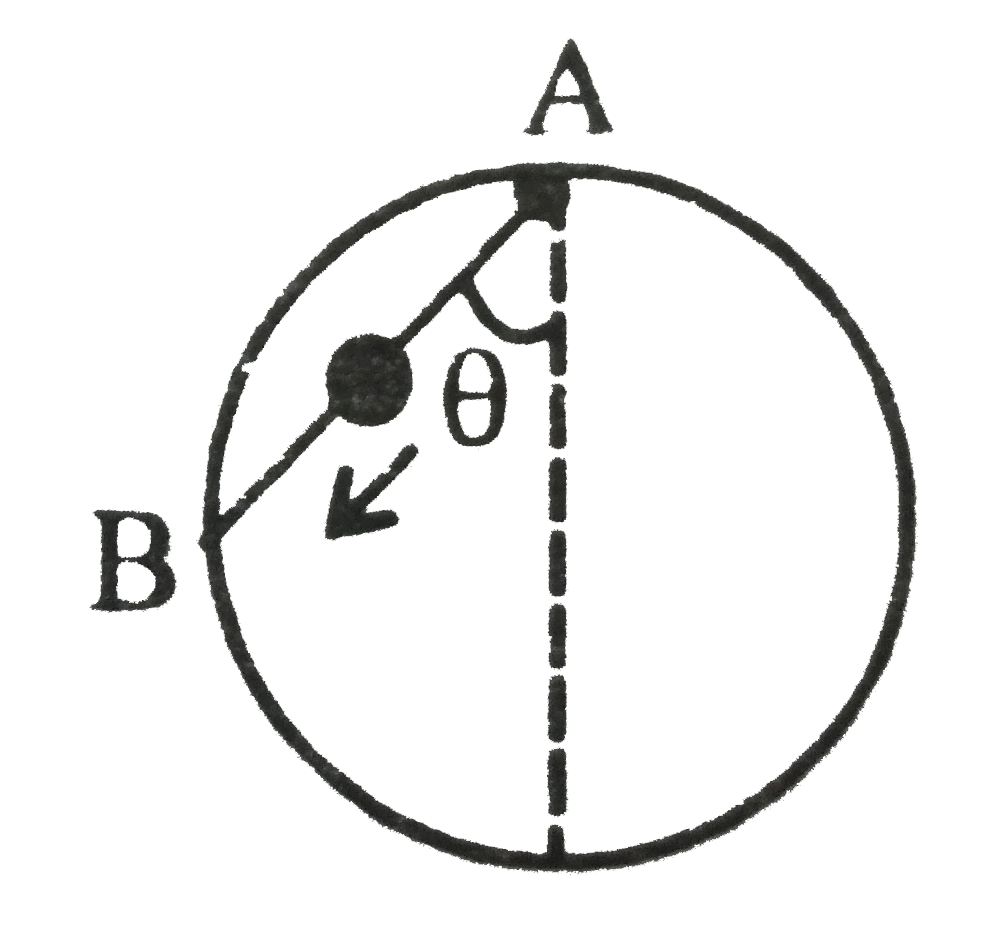
View SolutionTwo beads A and B of masses m1 and m2 respectively, are threaded on a smooth circular wire of radius a fixed in a vertical plane. B is stationary at the lowest point when A is gently dislodged from rest at the highest point. A collided with B at the lowest point. The impulse given to B due to collision is just great enough to carry it to the level of the centre of the circle while A is immediately brought to rest by the impact.
 What is the coefficient of restituting between the beads?
What is the coefficient of restituting between the beads?
View SolutionTwo beads A and B of masses m1 and m2 respectively, are threaded on a smooth circular wire of radius a fixed in a vertical plane. B is stationary at the lowest point when A is gently dislodged from rest at the highest point. A collided with B at the lowest point. The impulse given to B due to collision is just great enough to carry it to the level of the centre of the circle while A is immediately brought to rest by the impact.

Find the ratio m1:m2
View SolutionTwo beads A and B of masses m1 and m2 respectively, are threaded on a smooth circular wire of radius a fixed in a vertical plane. B is stationary at the lowest point when A is gently dislodged from rest at the highest point. A collided with B at the lowest point. The impulse given to B due to collision is just great enough to carry it to the level of the centre of the circle while A is immediately brought to rest by the impact.

If m2 again comes down and collides with m1 then after the collision
View Solution
