A bead is free to slide down a smooth wire tightly stretched between points and on a vertical circle. If the starts from rest at , the heighest point on the circle
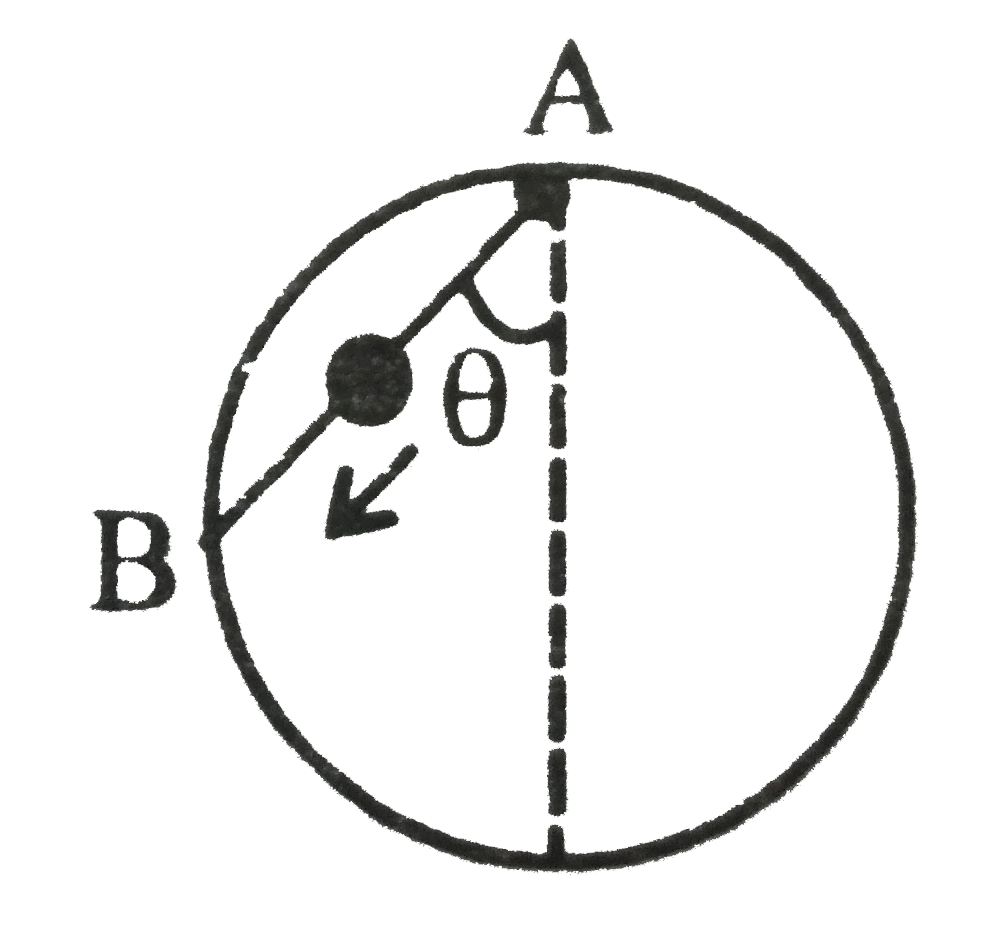
its velocity on arriving at is proportional to
its velocity on arriving at is proportional to
time to arrive at is proportional to
time to arrive at is independent of
The correct Answer is:A, D
(A)
(D)
Similar Questions
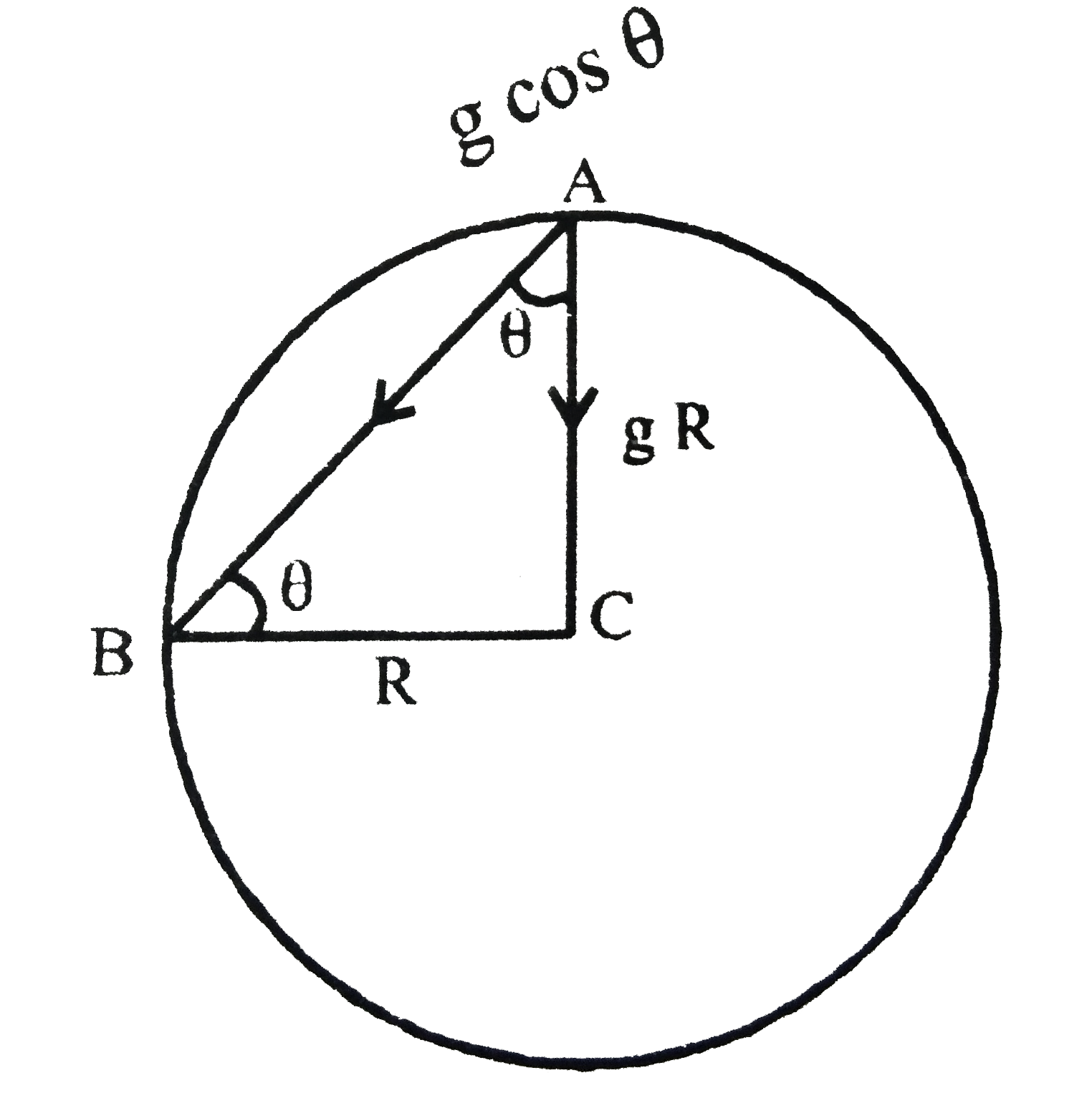
A bead is free to slide down on a smooth wire rightly stretched between points AandB on a vertical circle of radius 10m. Find the time (in sec) taken by the bead to reach point B, if the bead slides from rest from the highest point A on the circle.
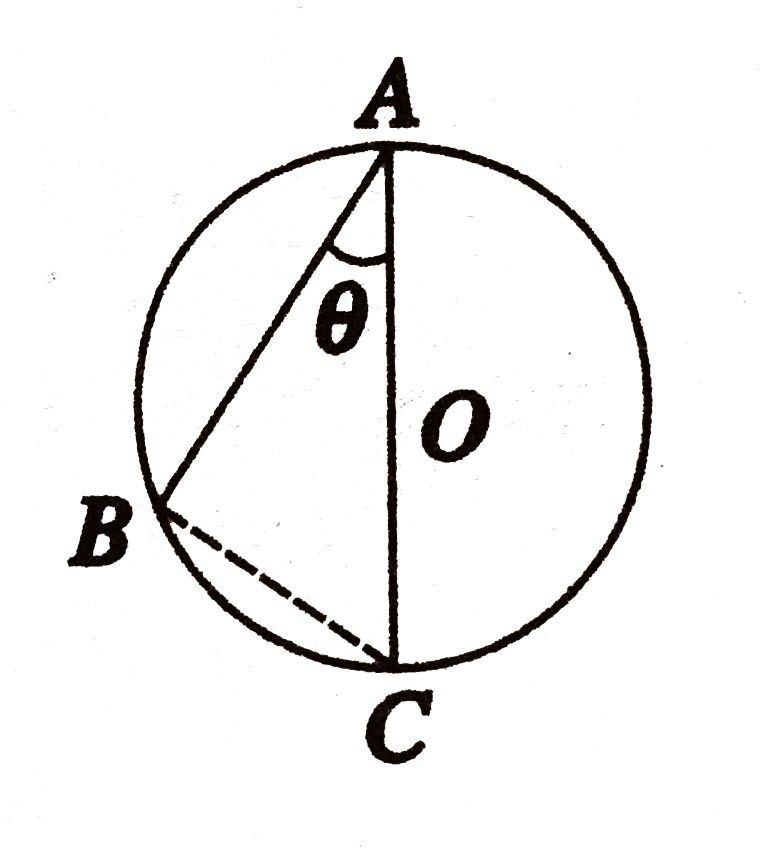 .
.
View SolutionA circular wire frame is fixed in a vertical plane. A smooth wire is tightly stretched between point P1andP2. A bead slides from the point P1 the highest point of the circle Determine (a) its velocity v when it arrives at P2 and (b) show that time to slide along any similar chord is same

View Solution
Knowledge Check
A bead is free to slide down a smooth wire tightly stretched between points A and on a verticle circle of radius R. if the bead starts from rest at 'A', the highest point on the circle, its velocity when it arrives at B is :-
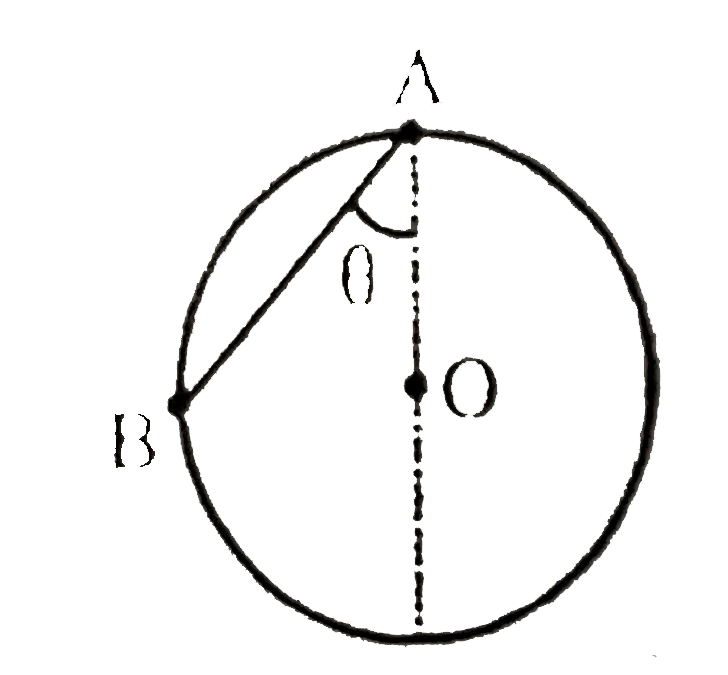 A2√gRB2√gRcosθC2√RgDNone of these
A2√gRB2√gRcosθC2√RgDNone of theseA bead is sliding down a smooth wire tightly stretched between the points P1 and P2 on a vertical circle of radius R. If the bead starts from rest from P1, the highest point on the circle and P2 lies anywhere on the circumference of the circle. Then
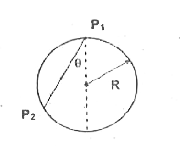 Atime taken by bead to go from P1 to P2 is dependent on position P2 and equals 2√RgcosθBtime taken by bead to go from P1 to P2 is independent of position P2 and equals 2√RgCAcceleration of bead along the wire is g cos θ.DVelocity of bead when it arrives at P2 is 2√gRcosθ.
Atime taken by bead to go from P1 to P2 is dependent on position P2 and equals 2√RgcosθBtime taken by bead to go from P1 to P2 is independent of position P2 and equals 2√RgCAcceleration of bead along the wire is g cos θ.DVelocity of bead when it arrives at P2 is 2√gRcosθ.A bead slides on a frictoinless strainght rod fixed between points A and B of a vertical circular loop of radius as shown in the figure. Line BC is a vertical diameter. Denoting acceleration due to gravity by g, which of the following is correct expression for the time taken by the bead to slide from A to B
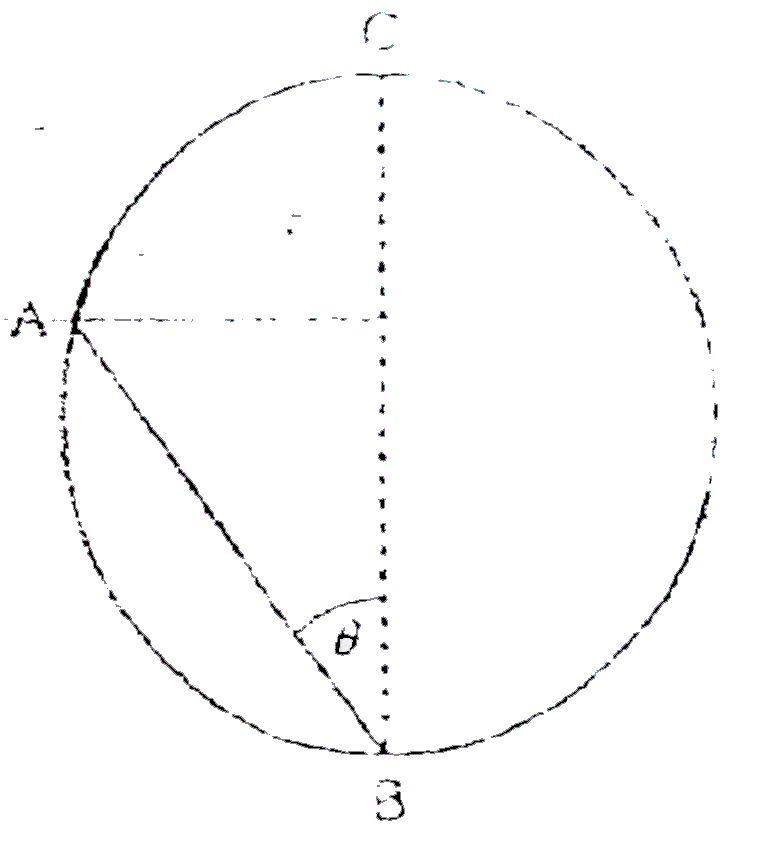 A√4rgB√4rgcosθC√4rtanθgD√4rcotθg
A√4rgB√4rgcosθC√4rtanθgD√4rcotθg
The time a body takes to slide down any smooth chord of a vertical circle, which is drawn from the highest point of the circle is constant.
View SolutionA heavy partile slides under gravity download the inside of a smooth vertical tube dheld in vertical plane. It starts from the highest point with velocity √2ag , where a is the radius of the circle. Find the angular position θ (as shown in figure) at which the vertical acceleration of the particle is maximum.
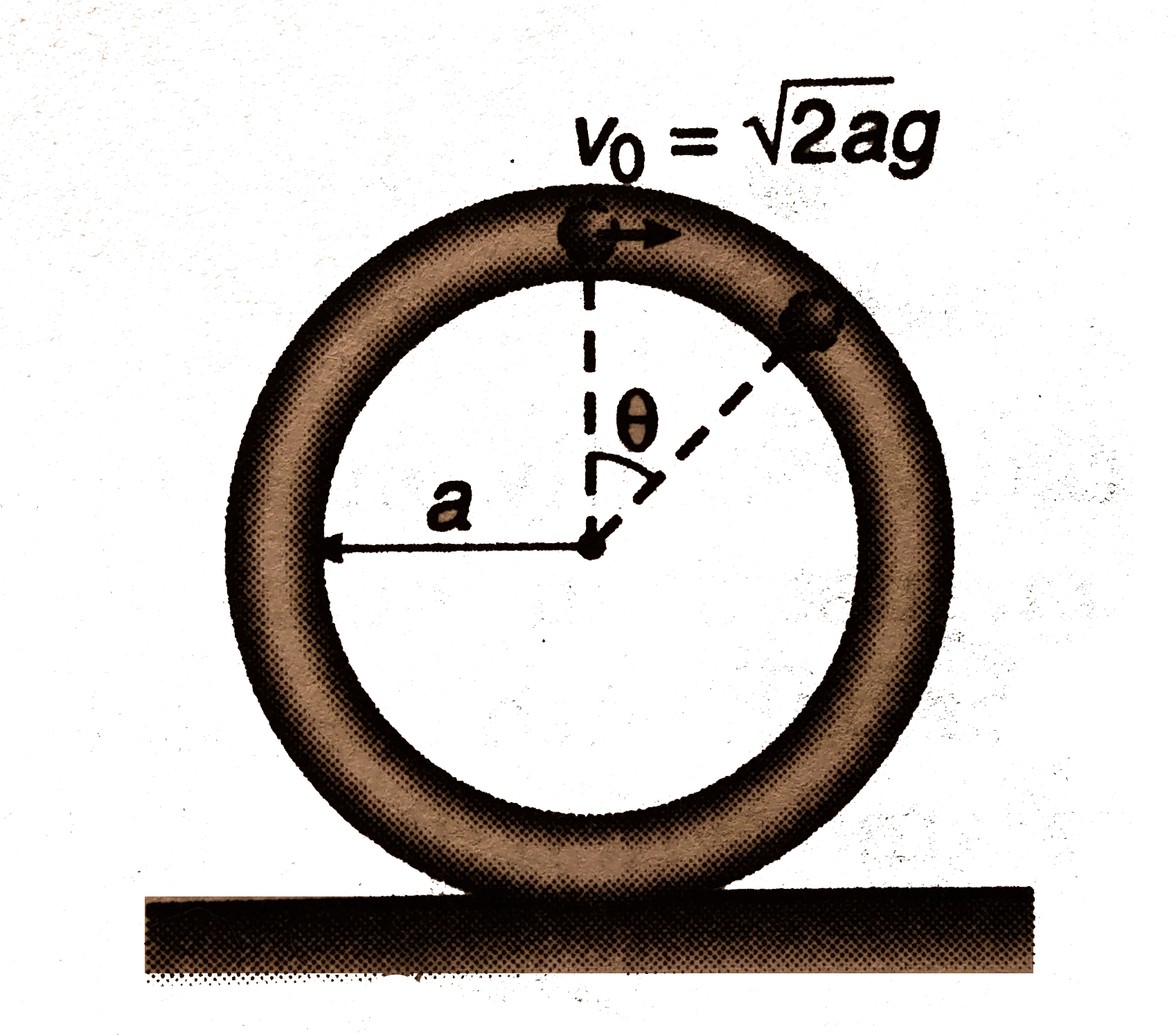
View SolutionA bead can slide on a smooth circular wire frame of radius r which is fixed in a vertical plane. The bead is displaced slighty from the highest point of the wire frame. The speed of the bead subsequently as a function of the angle θ made by the bead with the verticle line is
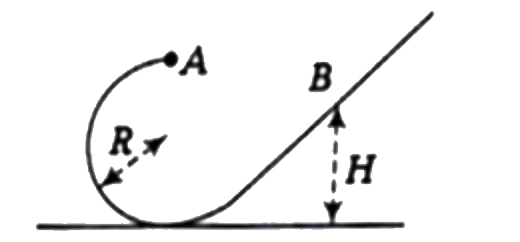
View SolutionA small bead of mass M slides on a smooth wire that is bent in a circle of radius R. It is released at the top of the circular part of the wire (point A in the figure) with a negligibly small velocity. Find the height H where the bead will reverse direction
View SolutionA bead can slide on a smooth circular wire frame of radius R which is fixed in a vartical plane. The bead is displaced slightly from the highest point of the wire frame. The speed of the bead subsequently as a function of the angle θ made by the bead with the vertical line is
View Solution
