A thin rod of length L is lying along the x-axis with its ends at x = 0 and x = L. Its linear density (mass/length) varies with x as k(xL)n where n can be zero or any positive number. If the position XCM of the centre of mass of the rod is plotted against n, which of the following graphs best approximates the dependence of XCM on n?
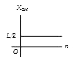
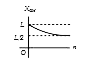
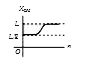
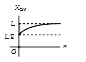
The correct Answer is:D
ρ=K(xL)n

COM=∫xdm∫dm=∫L0xk(xL)ndx∫k(xL)ndx
=k(L)n[xn+2n+2]L0k(Ln)[xn+1n+1]L0=n+1n+2.L
implies xCOM=(n+1n+2)L
At n=0 , xCOM=L2
At n=1, xCOM=23L
At n→∞,xCOM=L
Similar Questions
A thin rod of length L is lying along the x-axis with its ends at x=0 and x=L its linear (mass/length) varies with x as k(xL)n, where n can be zero of any positive number. If to position xCM of the centre of mass of the rod is plotted against 'n', which of the following graphs best apporximates the dependence of xCM on n?
View SolutionA thin rod of length L is lying on the X-axis with its end at x = 0 and x = L. Its linear density varies with x as K(x/L)^(n) , where n can be zero or any positive number. If the position of centre of mass of the rod is plotted against .n. which of the following graph best approximates the dependence of X_("cm") on n ?
View SolutionA thin rod of length L is lying along the x-axis with its ends at x = 0 and x = L. Its linear density (mass/length) varies with x as k(xL)n where n can be zero or any positive integer. If position Xcm of centre of mass of the rod is plotted against n, which of the following graphs best approximates the dependence of xCM on n?
View SolutionA thin rod of length L is placed along the x-axis with its ends at x = 0 and x = L. Its linear density (mass / length) k ((x)/(L))^(n) With x, where n can be zero or any positive number. If the position of the center of mass of the rod x_(CM), n Which of the following diagrams is denoted against x_(CM) Represents the dependence of?
View SolutionA rod of length L is placed along the x-axis between x=0 and x=L . The linear mass density (mass/length) rho of the rod varies with the distance x from the origin as rho=a+bx . Here, a and b are constants. Find the position of centre of mass of this rod.
View SolutionA non–uniform thin rod of length L is placed along x-axis as such its one of ends at the origin. The linear mass density of rod is lambda=lambda_(0)x . The distance of centre of mass of rod from the origin is :
View SolutionA non-uniform thin rod of length L is placed along X-axis such as one of its ends is at the origin. The linear mass density of rod is l =lamda_0x The distance of centre of mass of rod from- the origin is
View SolutionA thin rod of length 6 m is lying along the x-axis with its ends at x=0 and x=6m. Its linear density *mass/length ) varies with x as kx4. Find the position of centre of mass of rod in meters.
View Solution