A parallel plate capacitor is made of two dielectric blocks in series. One of the blocks has thickness and dielectric constant and the other has thickness and dielectric constant as shown in Figure. This arrangement can be thought as a dielectric slab of thickness and effective dielectric constant k. The k is :

The correct Answer is:C
The capacitance of parallel plate capacitor filled with dielectric block of thickness and dielectric constant is given by
Similarly, capacitance of parallel plate capacitor filled with dielectric block of thickness and dielectric constant is given by
Since the two capacitors are in series combination, the equivalent capacitance is given by
or
But the equivalent capacitances is given by
On comparing, we have
Similar Questions
वर्गाकार प्लेटों वाले एक समान्तर प्लेट संधारित्र को चित्रानुसार चार परावैद्युतों, जिनके परावैद्युतांक K1,K2,K3,K4 है, से भर दिया जाता है तो प्रभावी परावैद्युतांक K का मान होगा
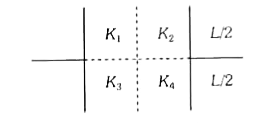
View SolutionA parallel plate capacitor is made of two dielectric blocks in series. One of the blocks has thickness d_(1) and dielectric constant K_(1) and the other has thickness d_(2) and dielectric constant K_(2) as shown in figure. This arrangement can be through as a dielectric slab of thickness d (= d_(1) + d_(2)) and effective dielectric constant K . The K is. .
View SolutionA parallel plate capacitor with square plates is filed with four dielectrics of dielectric constants K1,K2,K3,K4, arranged as shown in the figure. The effective dielectric constant K will be :
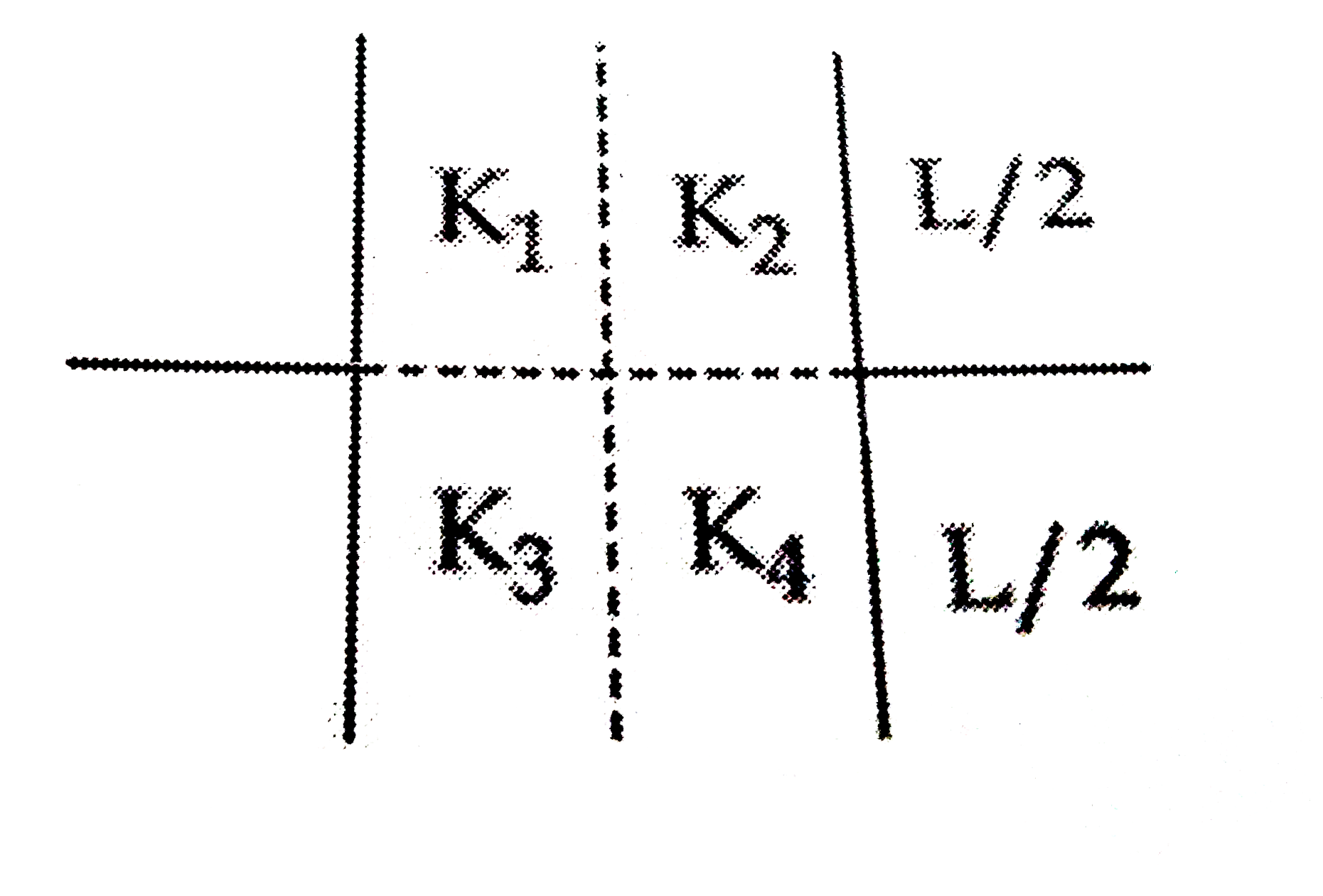
View SolutionA parallel plate capacitor is made of two dielectric blocks in series. One of the blocks has thickness d_(1) and dielectric constant K_(1) and the other has thickness d_(2) and dielectric constant K_(2) as shown in figure. This arrangement can be through as a dielectric slab of thickness d (= d_(1) + d_(2)) and effective dielectric constant K . The K is. .
View SolutionExplain Polarisation of dielectric slab. What is the effect on capacitance if we introduce a dielectric slab of dielectric Constant K in between parallel plate capacitor, thickness of slab is less than the separation between the plates.
View SolutionA parallel plate capacitor is made of two dielectric blocks in series. One of the blocks has thickness d_(1) and dielectric constant K_(1) and the other has thickness d_(2) and dielectric constant K_(2) as shown in figure. This arrangement can be through as a dielectric slab of thickness d (= d_(1) + d_(2)) and effective dielectric constant K . The K is. .
View SolutionFind the capacitance between A and B if two dielectric alabs (each of area A ) of dielectric constants K_(1) and K_(2) and thicknesses d_(1) and d_(2) are inserted between the plates of a parallel plate capacitor of plate area A . .
View SolutionFind the capacitance between A and B if three dielectric slabs of dielectric constants K_(1) area A _(2) and thickness d_(2) ) are inserted between the plates of a parallel late capacitor of plate area A. (Given that the distance between the two plates is d_(1)=d_(2)+d_(2) .) .
View Solution