A parallel plate capacitor is made of two dielectric blocks in series. One of the blocks has thickness d1 and dielectric constant K1 and the other has thickness d2 and dielectric constant K2 as shown in figure. This arrangement can be through as a dielectric slab of thickness d(=d1+d2) and effective dielectric constant K. The K is.
 .
.
K1d1+K2d2d1+d2
K1d1+K2d2K1+K2
K1+K2(d1+d2)(K1d1+K2d2)
2K1+K2K1+K2.
The correct Answer is:C
The capacitance of parallel plate capacitor filled with dielectriic block has thickness d1 and dielectric constant K2 is given by
C1=K1ε0Ad1
Similarly, capacitance of parallel plate capacitor filled with dielectric lbock has thickness d2 and dielectric constant K2 is given by
C2=K2ε0Ad2
Since, the two capacitors are in series combination, the equivalent capacitance is given by
1C=1C1+1C2
or
C=C1C2C1+C2=K1ε0Ad1K2ε0Ad2K1ε0Ad1+K2ε0Ad2=K1K2ε0AK1d2+K2d1 . . .(i)
But the equivalent capacitances is given by
C=Kε0Ad1+d2
On comparing we have
K=K1K2(d1+d2)K1d2+K2d1.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - MCQ s (More than one Options)
7 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Very short type question
5 Videos
- ELECTROMAGNETIC WAVESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - LONG ANSWER
5 Videos
- MAGNETISM AND MATTER BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - All Questions
24 Videos
Similar Questions
Between the plates of a parallel plate condenser, a plate of thickness t1 and dielectric constant k1 is placed. In the rest of the space, there is another plate of thickness t2 and dielectric constant k2. The potential difference across the condenser will be
View SolutionBetween the plates of a parallel plate condenser, a plate of thickness t1 and dielectric constant k1 is placed. In the rest of the space, there is another plate of thickness t2 and dielectric constant k2. The potential difference across the condenser will be
View SolutionA parallel plate capacitor with square plates is filed with four dielectrics of dielectric constants K1,K2,K3,K4, arranged as shown in the figure. The effective dielectric constant K will be :
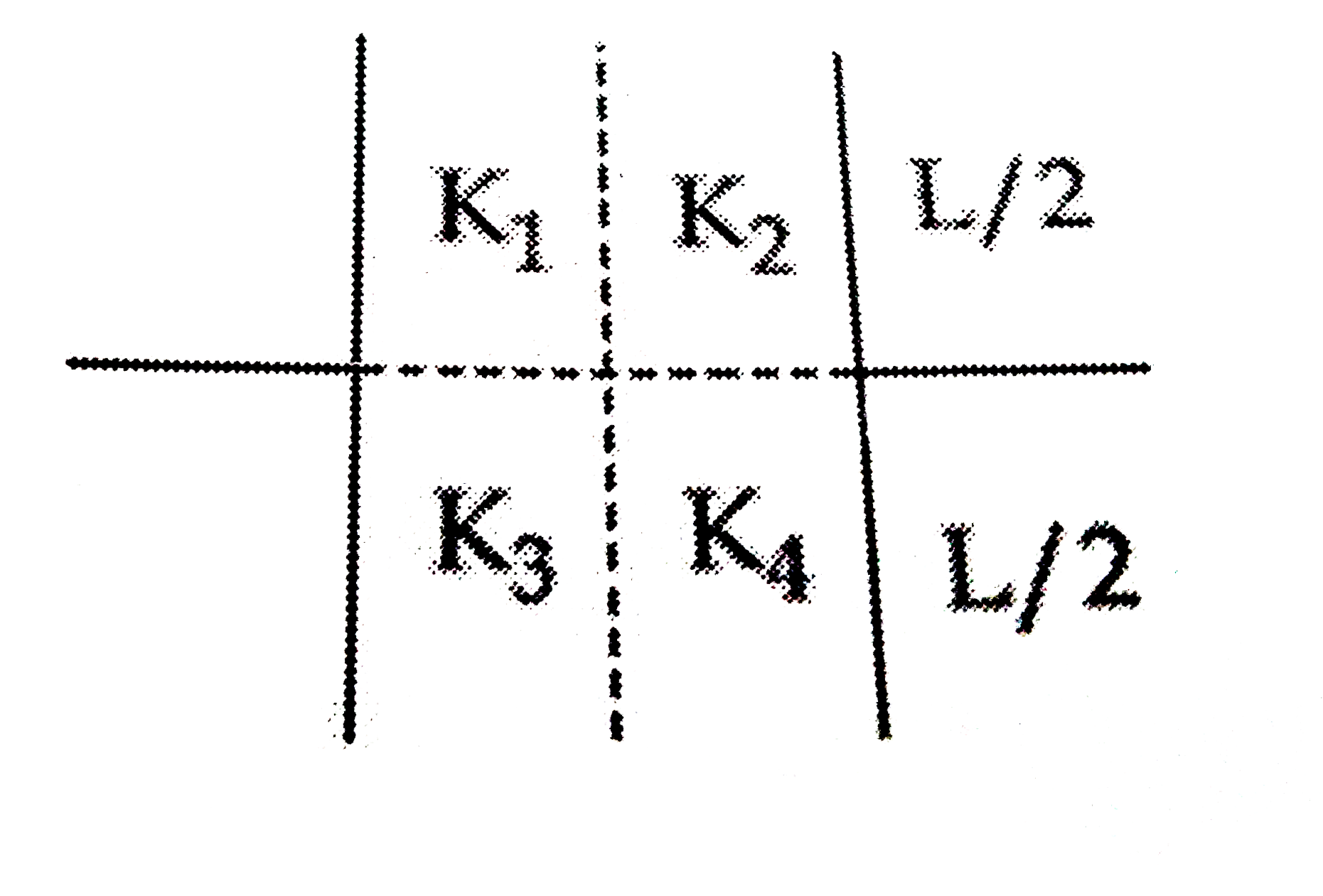
View SolutionA parallel plate capacitor of plate area A and separation d is filled with two materials each of thickness d2 and dielectric constants ∈1 and ∈2 respectively. The equivalent capacitance will be

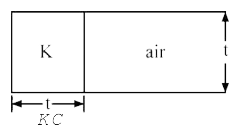
View SolutionA parallel plate capacitor with air as the dielectric has capacitance C. A slab of dielectric constant K and having the same thickness as the separation between plates is introduced so as to fill one-fourth of the capacitor as shown in the figure. The new capacitance will be :
View SolutionA parallel plate capacitor has plate area A and plate separation d. The space betwwen the plates is filled up to a thickness x (ltd) with a dielectric constant K. Calculate the capacitance of the system.

View SolutionFind the capacitance between A and B if two dielectric alabs (each of area A) of dielectric constants K1 and K2 and thicknesses d1 and d2 are inserted between the plates of a parallel plate capacitor of plate area A.
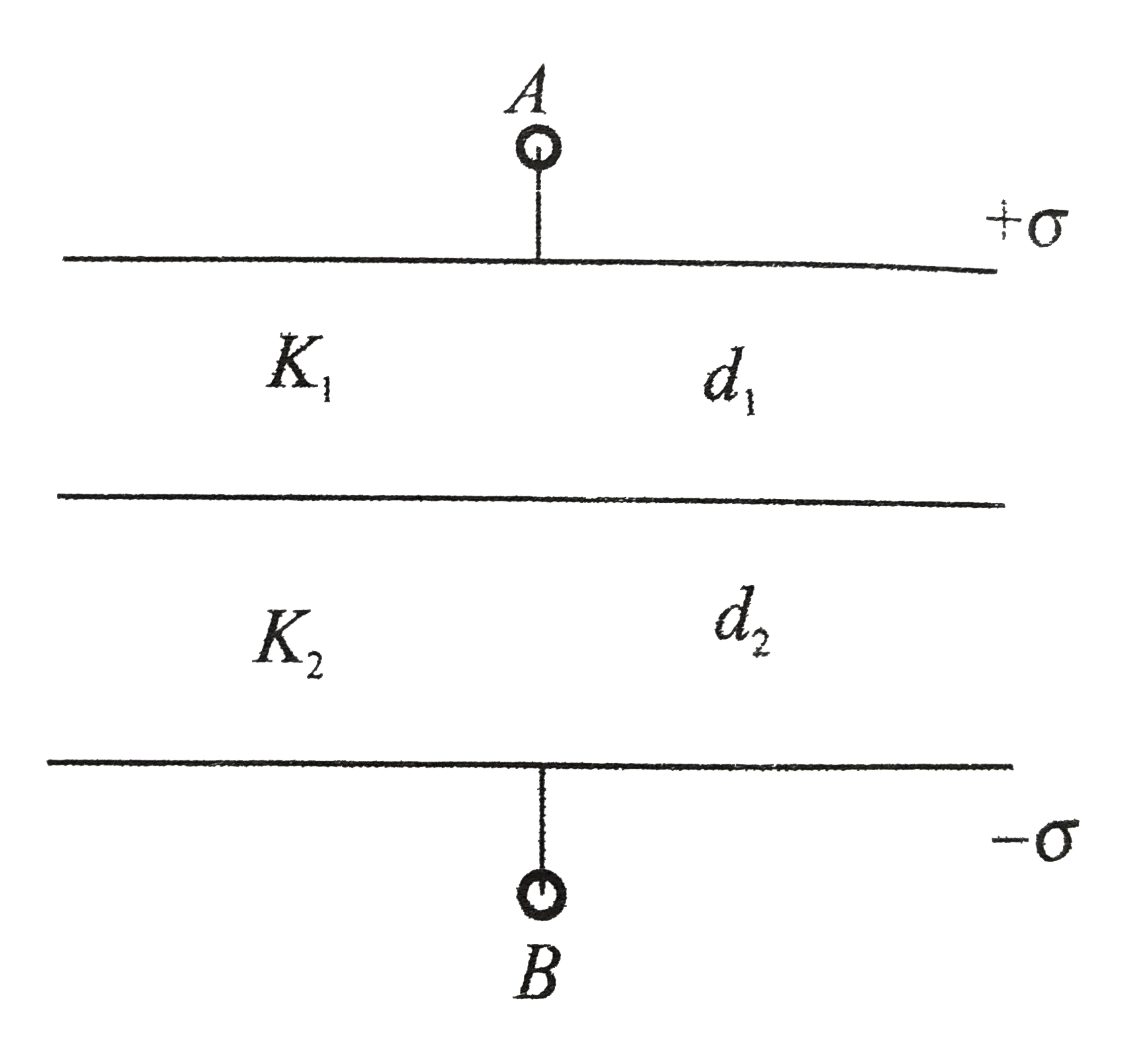 .
.
View SolutionFind the capacitance between A and B if two dielectric slabs (each of thickness d) of dielectric constants K1 and K2 and areas K1 and K2 and inserted between the plates of a parallel plate capacitor of plate area A.
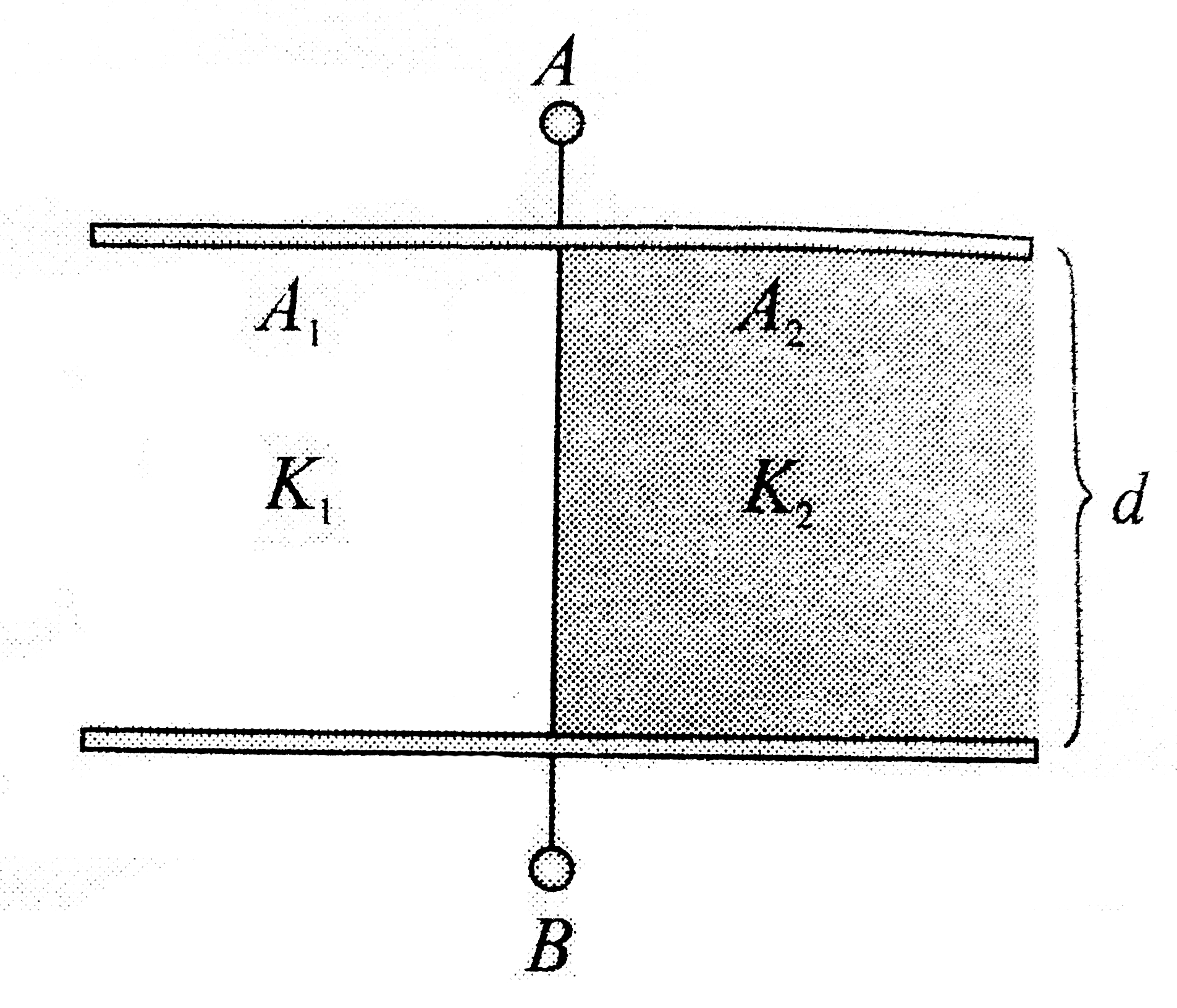 .
.
View SolutionA parallel plate air capacitor has capacitance C. Half of space between the plates is filled with dielectric of dielectric constant K as shown in figure . The new capacitance is C . Then
View SolutionA battery charges a parallel plate capacitor of thickness (d) so that an energy [U0] is stored in the system. A slab of dielectric constant (K) and thickness (d) is then introduced between the plates of the capacitor. The new energy of the system is given by
View Solution
