Two blocks each of mass m are connected to a spring of spring constant k. if both are given velocity v in opposite directions, then the maximum elongation of the spring is

$\sqrt{\frac{m v^{2}}{k}}$

$\sqrt{\frac{2 m v^{2}}{k}}$

$\sqrt{\frac{m v^{2}}{2 k}}$

$2 \sqrt{\frac{m v^{2}}{k}}$

Video Solution

Text Solution

Verified by Experts

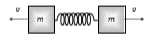
The correct Answer is:B

Law of conservation of energy-
$\frac{1}{2} m v^{2} + \frac{1}{2} m v^{2} = \frac{1}{2} k x^{2}$
$\Rightarrow m v^{2} = \frac{1}{2} k x^{2} \Rightarrow x = \sqrt{\frac{2 m v^{2}}{k}}$ .

Updated on:21/07/2023

Class 11 PHYSICS SIMPLE HARMONIC MOTION

Similar Questions

Two blocks are connected by a spring of natural length 2m.The force constant of spring is $200 N / m$ .Find spring force in following siturations.

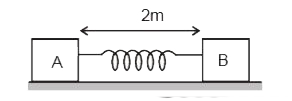
If block 'A' and 'B' both are displaced by 0.5 m in opposite direction
02:25
View Solution
Two blocks of masses m, and m, are connected to the ends of a spring of spring constant k. System is kept at rest on a frictionless horizontal floor with spring in its natural length. Both the blocks are pulled along opposite directions with forces of same magnitude F. Calculate maximum elongation of spring and distances travelled by the blocks during this motion.
View Solution
एक m द्रव्यमान का ब्लॉक एक k स्प्रिंग नियतांक की स्प्रिंग से चित्रानुसार जुड़ा है। ब्लॉक में महत्तम विस्थापन है
02:49
View Solution
जो गुटके में प्रत्येक का द्रव्यमान m है, इन्हें स्प्रिंग नियतांक k की स्प्रिंग से जोड़ा जाता गया है । यदि दोनों को विपरीत दिशाओं में वेग v दिया जाता है तब स्प्रिंग की लम्बाई में अधिकतम वृद्धि होगी।

03:50
View Solution
Two springs are connected to a block of mass M is placed on a frictionless surface as shown in figure. If both springs have a spring constant k, the frequency of oscillation of the block is………

02:22
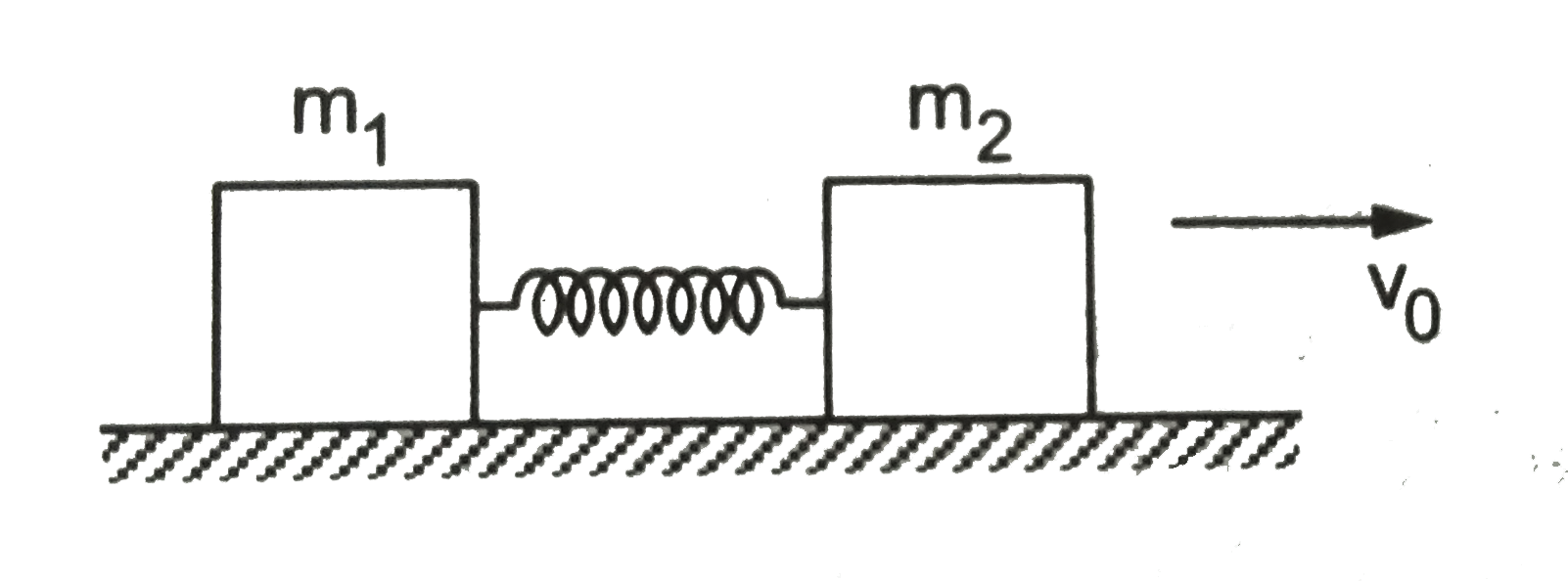
View Solution
Two blocks of masses $m_{1} and m_{2}$ are connected by a spring of spring constant k figure. The block of mass $m_{2}$ is given a shape impulse so that it acquires a velocity $v_{0}$ towards right. Find a. the velocity of the centre of mass b. the maximum elongation that the spring will suffer.

06:42
View Solution
Two identical blocks $A$ and $B$ , each of mass $m$ resting on smooth floor are connected by a light spring of natural length $L$ and spring constant $k$ , with the spring at its natural length. A third identical block $C$ (mass $m$ ) moving with a speed $v$ along the line joining $A$ and $B$ collides with $A$ . The maximum compression in the spring is
04:08
View Solution
Two blocks $A$ and $B$ . each of mass $m$ , are connected by a massless spring of natural length $I$ . and spring constant $K$ . The blocks are initially resting in a smooth horizontal floor with the spring at its natural length, as shown in Fig. A third identical block $C$ , also of mass $m$ , moves on the floor with a speed $v$ along the line joining $A$ and $B$ . and collides elastically with $A$ . Then

03:08
View Solution

Two blocks each of mass m are connected to a spring of spring constant k. if both are given velocity v in opposite directions, then the maximum elongation of the spring is

The correct Answer is:B

Law of conservation of energy- 1 2 m v 2 + 1 2 m v 2 = 1 2 k x 2 ⇒ m v 2 = 1 2 k x 2 ⇒ x = 2 m v 2 k .

Similar Questions

Recommended Questions

Law of conservation of energy-
$\frac{1}{2} m v^{2} + \frac{1}{2} m v^{2} = \frac{1}{2} k x^{2}$
$\Rightarrow m v^{2} = \frac{1}{2} k x^{2} \Rightarrow x = \sqrt{\frac{2 m v^{2}}{k}}$ .