A block is kept on an inclined plane of inclination θ of length l. the velocity of particle at the bottom of inclined is (the coefficient of friciton is μ)
√2gl(μcosθ−sinθ)
√2gl(sinθ−μcosθ)
√2g(sinθ+μcosθ)
√2g(cosθ+μsinθ)
The correct Answer is:B
a=g(sinθ−μcosθ),s=1
v2=u2+2as, u = 0
⇒v=√2as=√2gl(sinθ−μcosθ)
Similar Questions
A block of mass m is placed on a rough plane inclined at an angle θ with the horizontal. The coefficient of friction between the block and inclined plane is μ . Ifθ<tan−1(μ) , then net contact force exerted by the plane on the block is :
View SolutionA block of mass m is at rest on a rough inclined plane of angle of inclination θ. If coefficient of friction between the block and the inclined plane is μ, then the minimum value of force along the plane required to move the block on the plane is
View SolutionA frictionless inclined plane of length l having inclination θ is placed inside a lift which is accelerating downward with on acceleration a (<g). If a block is allowed to move down the inclined plane, from rest, then the time taken by the block to slide from top of the inclined plane to the bottom of the inclined plane is
View SolutionIf a block of mass m lying on a frictionless inclined plane of length L height h and angle of inclination theta , then the velocity at its bottom is
View SolutionA block of mass m is placed at rest on an inclination θ to the horizontal. If the coefficient of friction between the block and the plane is μ, then the total force the inclined plane exerts on the block is
View SolutionA block with a square base measuring a×a and height h, is placed on an inclined plane. The coefficient of friction is μ. The angle of inclination (θ) of the plane is gradually increased. The block will
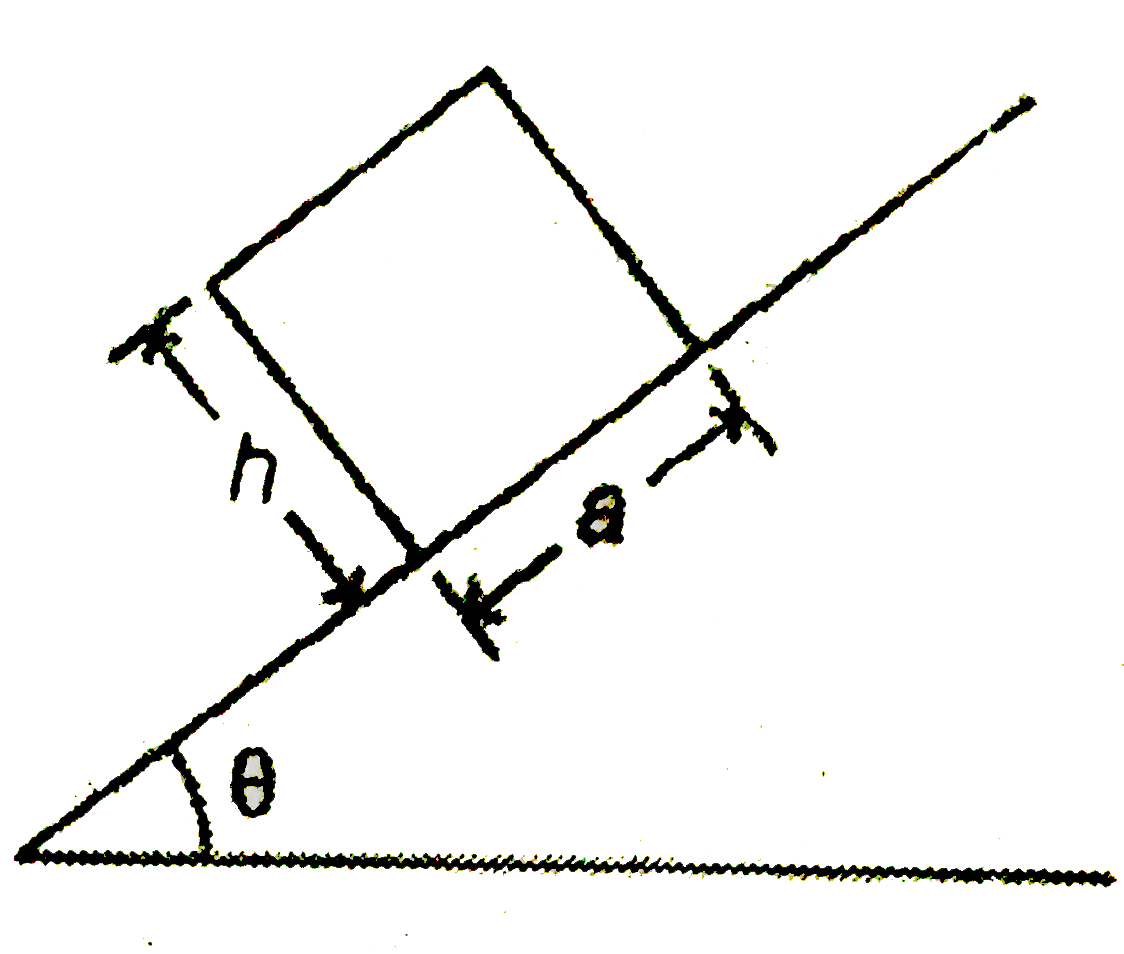
View SolutionThe coefficient of friction between the block and the inclined plane is μ.
View SolutionA block of mass m is at rest on a rough inclined plane of angle of inclination theta . If coefficient of friction between the block and the inclined plane is mu , then the minimum value of force along the plane required to move the block on the plane is
View Solution