A frictionless inclined plane of length l having inclination θ is placed inside a lift which is accelerating downward with on acceleration a (<g). If a block is allowed to move down the inclined plane, from rest, then the time taken by the block to slide from top of the inclined plane to the bottom of the inclined plane is
The correct Answer is:D
To solve the problem of a block sliding down a frictionless inclined plane inside a downward-accelerating lift, we can follow these steps:
1. Identify the Forces Acting on the Block:
- The block experiences gravitational force mg acting downward.
- The lift is accelerating downward with acceleration a (where a<g).
- The effective gravitational force acting on the block in the lift's frame is mg−ma=m(g−a).
2. Resolve the Effective Gravitational Force:
- The effective gravitational force can be resolved into two components relative to the inclined plane:
- Perpendicular to the incline: (g−a)cosθ
- Parallel to the incline: (g−a)sinθ
3. Determine the Acceleration of the Block:
- The acceleration aincline of the block down the incline is given by the component of the effective gravitational force acting parallel to the incline:
aincline=(g−a)sinθ
4. Use the Kinematic Equation to Find Time:
- The block starts from rest and slides down the incline of length L. We can use the kinematic equation:
s=ut+12at2
where:
- s=L (the length of the incline),
- u=0 (initial velocity),
- a=aincline=(g−a)sinθ.
Substituting these values into the equation gives:
L=0⋅t+12(g−a)sinθ⋅t2
Simplifying, we have:
L=12(g−a)sinθ⋅t2
5. Solve for Time t:
- Rearranging the equation to solve for t2:
t2=2L(g−a)sinθ
- Taking the square root to find t:
t=√2L(g−a)sinθ
Final Answer:
The time taken by the block to slide from the top of the inclined plane to the bottom is:
t=√2L(g−a)sinθ
- The block experiences gravitational force mg acting downward.
- The lift is accelerating downward with acceleration a (where a<g).
- The effective gravitational force acting on the block in the lift's frame is mg−ma=m(g−a).
- The effective gravitational force can be resolved into two components relative to the inclined plane:
- Perpendicular to the incline: (g−a)cosθ
- Parallel to the incline: (g−a)sinθ
- The acceleration aincline of the block down the incline is given by the component of the effective gravitational force acting parallel to the incline:
aincline=(g−a)sinθ
- The block starts from rest and slides down the incline of length L. We can use the kinematic equation:
s=ut+12at2
where:
- s=L (the length of the incline),
- u=0 (initial velocity),
- a=aincline=(g−a)sinθ.
L=0⋅t+12(g−a)sinθ⋅t2
Simplifying, we have:
L=12(g−a)sinθ⋅t2
- Rearranging the equation to solve for t2:
t2=2L(g−a)sinθ
- Taking the square root to find t:
t=√2L(g−a)sinθ
The time taken by the block to slide from the top of the inclined plane to the bottom is:
t=√2L(g−a)sinθ
Topper's Solved these Questions
- LAW OF MOTIONBOOK - NARAYNACHAPTER - LAW OF MOTIONEXERCISE - EXERCISE - III
20 Videos
- KINETIC THEORY OF GASESBOOK - NARAYNACHAPTER - KINETIC THEORY OF GASESEXERCISE - LEVEL-III(C.W)
52 Videos
- MATHEMATICAL REVIEW & PHYSICAL WORLDBOOK - NARAYNACHAPTER - MATHEMATICAL REVIEW & PHYSICAL WORLDEXERCISE - C.U.Q
13 Videos
Similar Questions
A block is released from top of a smooth inclined plane.It reaches the bottom of the plane in 6 sec.The time taken by the body to cover the first half of the inclined plane is:
View SolutionA block is placed on an inclined plane moving towards right with an acceleration a0=g The length of the inclined plane is l0. All the surfaces are smooth Find the time taken by the block to reach from bottom to top.
 .
.
View Solution
Knowledge Check
A smooth inclined plane of length L, having an inclination θ with horizontal is inside a lift which is moving down with retardation a. The time taken by a block to slide down the inclined plane from rest will be
A√2L√asinθB√2LgsinθC√2L(g−a)sinθD√2L(g+a)sinθA smooth inclined plane of length L having inclination θ with the horizontal inside a lift which is moving down with retardation α . The time taken by a body to slide down the inclined plane, from rest, will be
A√2LgsinθB√2LαsinθC√2L(g+α)sinθD√2L(g−α)sinθThe acceleration of 10kg block on the inclined plane is
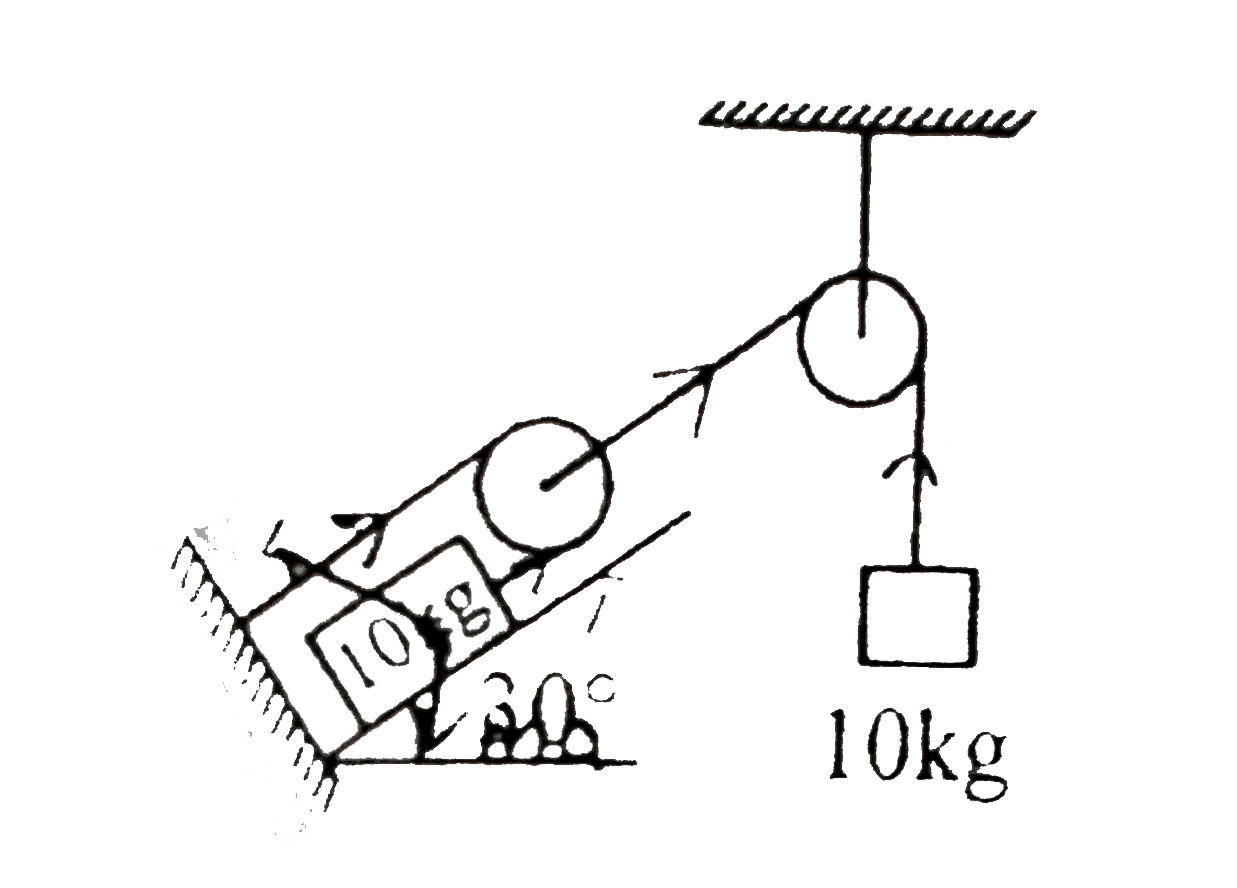 AzeroB4m/s2C6m/s2DNone of these
AzeroB4m/s2C6m/s2DNone of these

A block is released from the top of the smooth inclined plane of height h. Find the speed of the block as it reaches the bottom of the plane.
View SolutionA body is slipping from an inclined plane of height h and length l . If the angle of inclination is θ , the time taken by the body to come from the top to the bottom of this inclined plane is
View SolutionA body of mass m is placed over a smooth inclined plane of inclination θ, which is placed over a lift which is moving up with an acceleration a0 . Base length of the inclined plane is L. Calculate the velocity of the block with respect to lift at the bottom, if it is allowed to slide down from the top of the plane from rest :-
View SolutionA body of mass m is placed over a smooth inclined plane of inclination theta. Which iis placed over a lift which is moving up with an acceleration a0 . Base length o f the inclined plane is L . Calculate the velocity of the block with respect to lift at the bottom, if it is allowed to slide down from the top o fthe plane from rest.
View SolutionAn inclined plane of height h and length l have the angle of inclination θ. The time taken by a body to come from the top of the bottom of this inclined plane will be
View Solution
