A particle at a distance of 1 m from the origin starts moving such that dr/dθ=r, where (r,θ) are polar coordinates. Then the angle between resultant velocity and tangential velocity component is
30 degrees
45 degrees
60 degrees
Dependent on where the particle is
The correct Answer is:B
drdθ=r=dsdθ⇒drdt=dsdt⇒vt=vr So, α=45∘
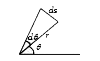
Similar Questions
A particle is moving in a circle of radius r with constant angular velocity omega . At any point (r, theta ) on its path , its position vector is vec(r ) = r cos theta hat(i) + r sin theta hat(j) . Show that the velocity of the particle has no component along the radius.
View SolutionIf the angle (theta) between velocity vector and the acceleration vector of a moving particle is 90^(@) lt theta lt 180^(@) , then the path of the particle is
View SolutionA point object moves along an arc of a circle of radius 'R'. Its velocity depends upon the distance covered 'S' as V = K√S where 'K' is a constant. If ' theta' is the angle between the total acceleration and tangential acceleration, then
View SolutionA point object moves along an arc of a circle of radius 'R'. Its velocity depends upon the distance covered 'S' as V=K sqrtS where 'K' is a constant. If ' theta ' is the angle between the total acceleration and tangential acceleration, then
View SolutionA point object moves along an arc of a circle of radius .R.. Its velocity depends upon the distance covered .S. as V=K√S where .K. is a constant. If .θ. is the angle between the total acceleration and tangential acceleration then
View SolutionA point moves along an arc of a circle of radius R. its velocity depends upon the distance covered as V=a√S where a = constant. The angle θ between the vector of total acceleration and tangential acceleration
View SolutionA Point moves along an arc of a circle of radius R. Its velocity depends upon the distance covered as V=√ where a=constant. The angle θ between the vector of total acceleration and tangential acceleration is
View SolutionA cyclist moving with a velocity r r from the horizontal while moving on a path of radius theta makes an angle, where cot theta = ………. it happens.
View Solution