A particle is moving an a cirle of radius 'r' and centre O with constant speed . What is the change in velocity in moving from A to B ?
(If any angle between two velocity vector is .)
The correct Answer is:B
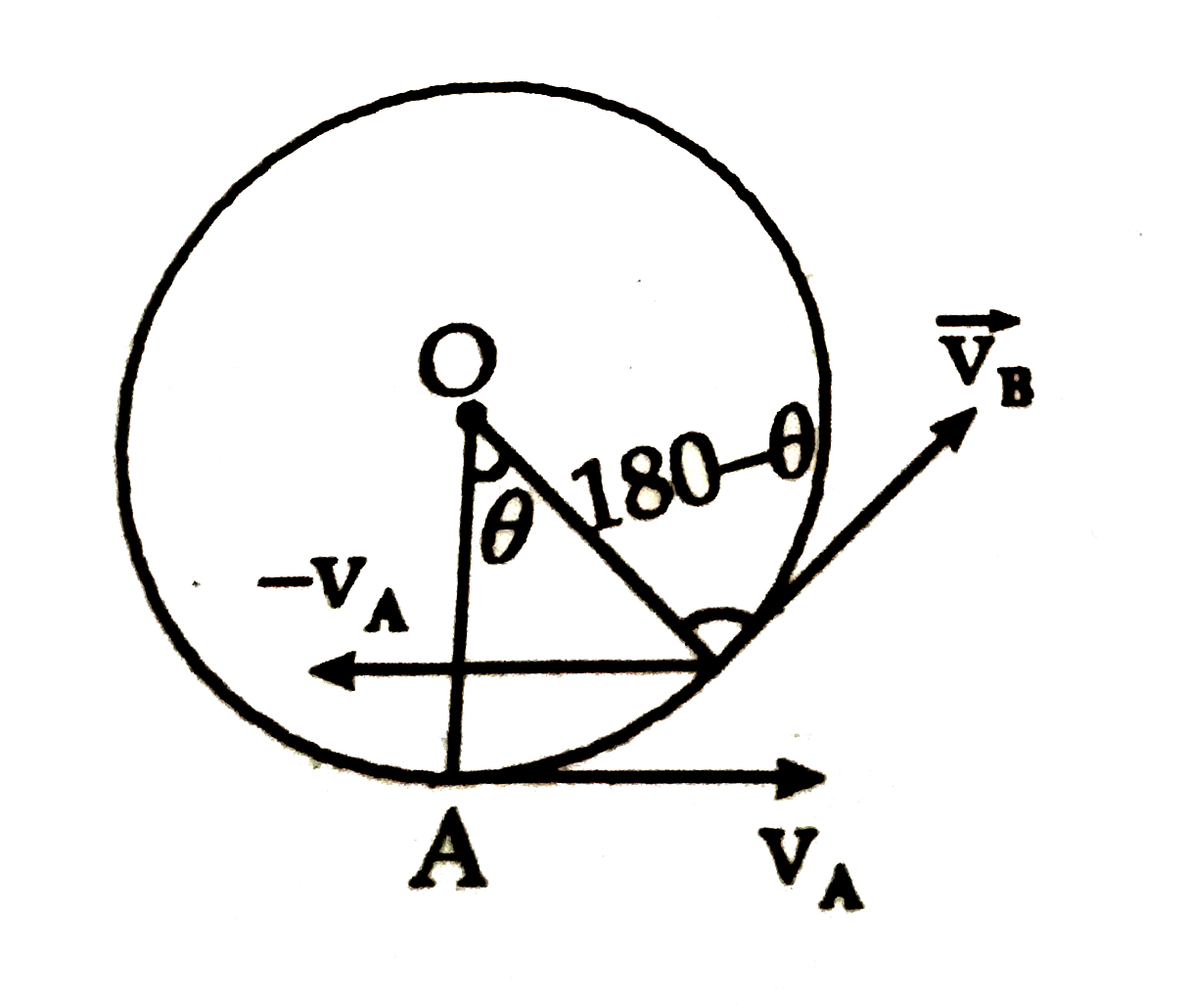
change in velocity
The angle between
Topper's Solved these Questions
Similar Questions
In Fig. a particle is moving in a circle of radius r centred at O with constant speed v. what is the change in velocity in moving from A to B ? Given ∠AOB=40∘.
View SolutionA particle is moving in a circle of radius having centre at 0. with a constant speed V. The magnitude at change in velocity in moving from A to B is 60°
View Solution
Knowledge Check
A particle is moving in a circle of radius r centred at O with constant speed v. What is the change in velocity in moving from A to B (∠AOB=40∘) ?
A2vsin20∘B4vsin40∘C2vsin40∘Dvsin20∘A particle is moving in a circle of radius r having centre at O with a constant speed v . The magnitude of change in velocity in moving from A to B is
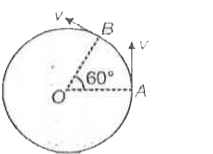 A2 vBZeroC√3vDv
A2 vBZeroC√3vDvA particle is moving in a circle of radius r with speed v as shown in the figure. The magnitude of change in velocity in moving from P to Q is
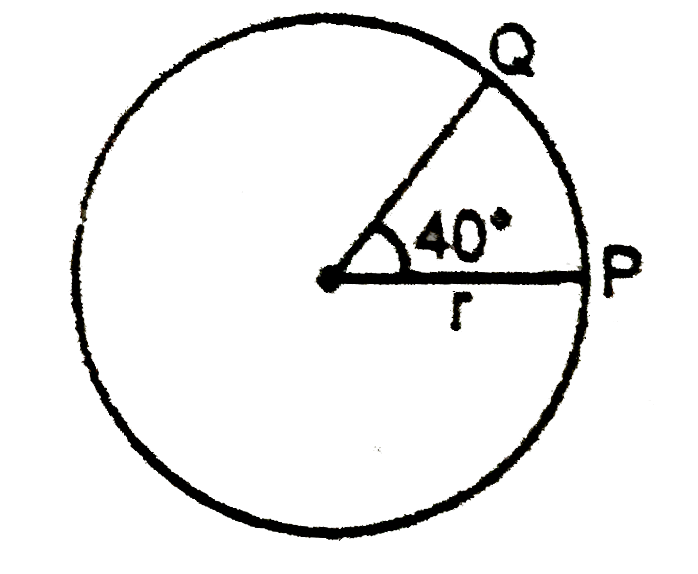 A2vcos40∘B2vsin40∘C2vcos20∘D2vsin20∘
A2vcos40∘B2vsin40∘C2vcos20∘D2vsin20∘
A particle is moving in a circle of radius r with speed v as shown in the figure. The magnitude of change in velocity in moving from P to Q is
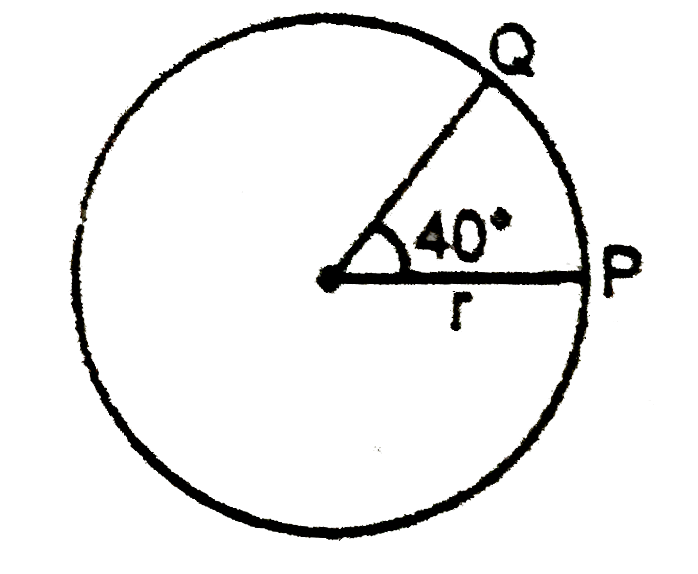
View SolutionA particle is moving on a circular path with a constant speed 'v'. Its change of velocity as it moves from A to B is:

View SolutionIf the body is moving in a circle of radius r with a constant speed v , its angular velocity is
View SolutionA particle is moving on a circular path with constant speed v. The magnitude of the change in its velocity after it has described an angle of 90∘ is :
View SolutionA particle is moving on a circular path of radius R with constant speed v. During motion of the particle form point A to point B

View Solution
