A particle is moving in a circle of radius R and its speed is given by v=λt2, where λ is a constant. Find (a) radial acceleration, (b) tangential acceleration, ( c) resultant acceleration and (d) angle between acceleration and velocity.
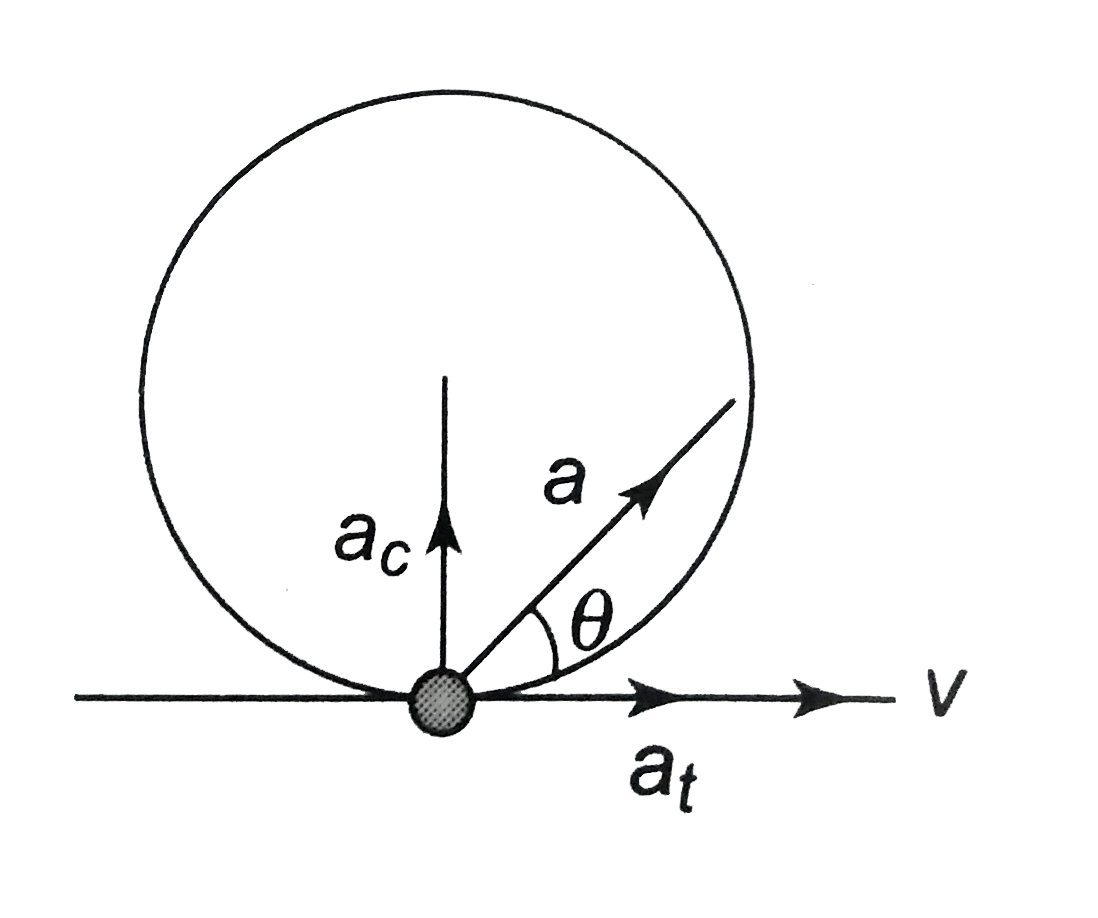
ac=(v2R)=(λt2)2R=λ2t4R
v=λt2
at=dvdt=2λt
a=√a2c+a2t
=√(λ2t4R)2+(2λt)2
tanθ=acat=(λ2t4R)2λt=λt32R
θ=tan−1(λt32R)
where θ is the angle between acceleration and velocity.
Topper's Solved these Questions
Similar Questions
A particle moves in a circle of radius 20 cm. Its linear speed is given by v=(3t2+5t) where t is in second and v is in m/s. Find the resultant acceleration at t = 1s.
View SolutionA particle moves in a circle of radius 20 cm Its linear speed is given by upsilon = 2 t where t is in second and upsilon in metre/second Find the radial and tangential acceleration at t=3s.
View Solution
Knowledge Check
A particle moves in a circle of radius 20 cm. Its linear speed is given by v=2t, where t is in second and v in metre/ second. Find the radial and tangential acceleration at t=3s.
A10ms2 , 2ms2B100ms2 , 12ms2C100ms2 , 5ms2D180ms2 , 2ms2A particle moves in a circle of radius 30cm. Its linear speed is given by v=2t, where t in second and v in m/s. Find out its radial and tangential acceleration at t=3s.
A220ms2,50m/s2B100m/s2,5m/s2C120m/s2D110m/s2,10m/s2A particle moves in a circle of radius 2 cm at a speed given by v =4t, where v is in cms ^-1 and t in seconds. The tangential acceleration at t =1s and total acceleration at t =1s are respiccitively .
A6cms−2and5cms−2B4cms−2and4√5 cms−2C5cms−2and5√5 cms−2DNone of these
A particle moves in a circle of radius 2cm at a speed given by v=4t, where v is in cms−1 and t is in seconds.
(a) Find the tangential acceleration at t=1s
(b) Find total acceleration at t=1s.
View SolutionA particle is moving such that the velocity is given by v=√2γs, where γ is constant and s is diplacement. Find the acceleration.
View SolutionA particle moves in circle of radius 1.0 cm at a speed given by v=2.0 t where v is in cm/s and t in seconeds. A. find the radia accelerationof the particle at t=1 s. b. Findthe tangential acceleration at t=1s. c.Find the magnitude of the aceleration at t=1s.
View SolutionA particle moves in a circle of radius 20 cm. Its linear speed is given by v=2t where t is in s and v in m/s. Then
a) the radial acceleration at t=2s is 80ms−2
b) tangential acceleration at t−2s is 2ms−2
c)net acceleration at t=2s is greater than 80ms−2
d) tangential acceleration remains constant in magnitude.
View SolutionThe speed of a particle moving in a circle of radius r=2m varies with time t as v=t2, where t is in second and v in m/s. Find the radial, tangential and net acceleration at t=2s.
View Solution

