5 cells, each of emf 0.2V and internal resistance 1Ω are connected to an external circuit of resistance of 10Ω. Find the current through external circuit-
12.5A
110A
115A
12A
The correct Answer is:C
To find the current through the external circuit with the given cells, we can follow these steps:
Step 1: Determine the total EMF of the cells
Since the cells are connected in series, the total EMF (E_total) is the sum of the individual EMFs of the cells.
Given:
- Each cell has an EMF of 0.2 V.
- There are 5 cells.
Etotal=5×0.2V=1.0V
Step 2: Determine the total internal resistance
The internal resistance of each cell is given as 1 Ω. Since they are connected in series, the total internal resistance (R_internal) is the sum of the individual internal resistances.
Given:
- Internal resistance of each cell = 1 Ω
- Number of cells = 5
Rinternal=5×1Ω=5Ω
Step 3: Calculate the total resistance in the circuit
The total resistance in the circuit (R_total) is the sum of the total internal resistance and the external resistance (R_external).
Given:
- External resistance (R_external) = 10 Ω
Rtotal=Rinternal+Rexternal=5Ω+10Ω=15Ω
Step 4: Use Ohm's Law to find the current
Ohm's Law states that the current (I) in a circuit is equal to the total voltage (E_total) divided by the total resistance (R_total).
I=EtotalRtotal=1.0V15Ω=115A
Final Answer
The current through the external circuit is 115A.
---
Since the cells are connected in series, the total EMF (E_total) is the sum of the individual EMFs of the cells.
- Each cell has an EMF of 0.2 V.
- There are 5 cells.
The internal resistance of each cell is given as 1 Ω. Since they are connected in series, the total internal resistance (R_internal) is the sum of the individual internal resistances.
- Internal resistance of each cell = 1 Ω
- Number of cells = 5
The total resistance in the circuit (R_total) is the sum of the total internal resistance and the external resistance (R_external).
- External resistance (R_external) = 10 Ω
Ohm's Law states that the current (I) in a circuit is equal to the total voltage (E_total) divided by the total resistance (R_total).
The current through the external circuit is 115A.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - ERRORLESSCHAPTER - CURRENT ELECTRICITYEXERCISE - NCERT BASED QUESTIONS (DIFFERENT MEASURING INSTRUMENTS)
74 Videos
- CURRENT ELECTRICITYBOOK - ERRORLESSCHAPTER - CURRENT ELECTRICITYEXERCISE - NCERT BASED QUESTIONS (HEATING EFFECT OF CURRENT)
67 Videos
- CURRENT ELECTRICITYBOOK - ERRORLESSCHAPTER - CURRENT ELECTRICITYEXERCISE - NCERT BASED QUESTIONS (Grouping of Resistances)
69 Videos
- ATOMIC AND NUCLEAR PHYSICSBOOK - ERRORLESSCHAPTER - ATOMIC AND NUCLEAR PHYSICSEXERCISE - Assertion and Reason
23 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - ERRORLESSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - ASSERTION & REASON
20 Videos
Similar Questions
Three identical cells, each of emf 2 V and internal resistance 0.2Ω are connected in series to an external resistor of 7.4Ω. Calculate the current in the circuit.
View SolutionThree identical cells of emf 4V with 1Ω internal resistance each are connected in series to an external resistance of 6Ω. Find the current flowing in the circuit.
View Solution
Knowledge Check
24 cells of emf 1.5V each having internal resistance of 1Ω are connected to an external resistance of 1.5Ω. To get maximum current,
Aall cells are connected in series combinationBall cells are connected in parallel combinationC4 cells in each row are connected in series and 6 such rows are connected in parallelD6 cells in each row are connected in series and 4 such rows are connected in parallelFour cell each of emf 2 V and internal resistance 1 ohm are connected n parallel with an external resistance of 6 ohm. The current in the external resistance is
A0.32 AB0.16 AC0.2 AD0.6 AFour cells, each of emf E and internal resistance r, are connected in series across an external resistance reverse. Then, the current in the external circuit is
A2E4r+RB3E4r+RC3E3r+RD2E3r+R
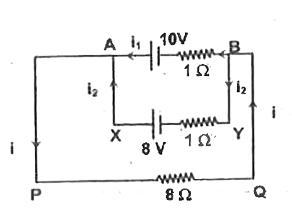
Two cells having emf's of 10 V and 8 V, and internal resistance of 1Ω(each) are connected as shown with an external resistance of 8Ω Find the current flowing through the circuit.
View SolutionThree identical, each of emf 2 V and internal resistance 0.2Ω are connected in series to an external resistor of 7.4Ω. Calculate the current in the circuit.
View SolutionA battery of 6 V internal resistance 0.5Ω is joined in parallel with another of 10 V and internal resistnace 1Ω. The combination sends a current through an external resistance of 12Ω. Find the current through each battery.
View SolutionA battery of emf 6 volts and internal resistance 1Ω is connected in parallel to another battery of emf 8V and internal resistance 2Ω. The combination is then used to send current through an external resistance of 10Ω. Find the current through the external resistance.
View SolutionA cell of e.m.f. 2 V and internal resistance 2Ω and an external resistance 18Ω forms closed circuit. The current through the circuit is
View Solution
