A battery of 6 V internal resistance 0.5Ω is joined in parallel with another of 10 V and internal resistnace 1Ω. The combination sends a current through an external resistance of 12Ω. Find the current through each battery.
To solve the problem, we need to analyze the circuit formed by the two batteries and the external resistor. We will use Kirchhoff's laws to find the currents through each battery.
1. Identify the Components:
- Battery 1 (E1): Voltage = 6 V, Internal Resistance (r1) = 0.5 Ω
- Battery 2 (E2): Voltage = 10 V, Internal Resistance (r2) = 1 Ω
- External Resistance (R) = 12 Ω
2. Assume Current Directions:
- Let I1 be the current flowing from Battery 1 (6 V).
- Let I2 be the current flowing from Battery 2 (10 V).
- The total current flowing through the external resistance R will be I_total = I1 + I2.
3. Apply Kirchhoff's Voltage Law (KVL):
- For the loop involving Battery 1 (E1):
−E1+I1⋅r1+Itotal⋅R=0
Substituting values:
−6+I1⋅0.5+(I1+I2)⋅12=0
Rearranging gives:
12I1+12I2+0.5I1=6
Simplifying:
12.5I1+12I2=6(Equation 1)
- For the loop involving Battery 2 (E2):
−E2+I2⋅r2+Itotal⋅R=0
Substituting values:
−10+I2⋅1+(I1+I2)⋅12=0
Rearranging gives:
12I1+13I2=10(Equation 2)
4. Solve the Equations:
- We have the two equations:
1. 12.5I1+12I2=6
2. 12I1+13I2=10
- To eliminate one variable, we can multiply Equation 1 by 13 and Equation 2 by 12:
162.5I1+156I2=78(Equation 3)
144I1+156I2=120(Equation 4)
- Now, subtract Equation 4 from Equation 3:
(162.5I1−144I1)+(156I2−156I2)=78−120
18.5I1=−42
I1=−4218.5≈−2.27 A
5. Determine I2:
- Substitute I1 back into Equation 2:
12(−2.27)+13I2=10
−27.24+13I2=10
13I2=37.24
I2≈2.86 A
Final Answer:
- Current through Battery 1 (I1) = -2.27 A (indicating it flows in the opposite direction)
- Current through Battery 2 (I2) = 2.86 A
- Battery 1 (E1): Voltage = 6 V, Internal Resistance (r1) = 0.5 Ω
- Battery 2 (E2): Voltage = 10 V, Internal Resistance (r2) = 1 Ω
- External Resistance (R) = 12 Ω
- Let I1 be the current flowing from Battery 1 (6 V).
- Let I2 be the current flowing from Battery 2 (10 V).
- The total current flowing through the external resistance R will be I_total = I1 + I2.
- For the loop involving Battery 1 (E1):
−E1+I1⋅r1+Itotal⋅R=0
Substituting values:
−6+I1⋅0.5+(I1+I2)⋅12=0
Rearranging gives:
12I1+12I2+0.5I1=6
Simplifying:
12.5I1+12I2=6(Equation 1)
−E2+I2⋅r2+Itotal⋅R=0
Substituting values:
−10+I2⋅1+(I1+I2)⋅12=0
Rearranging gives:
12I1+13I2=10(Equation 2)
- We have the two equations:
1. 12.5I1+12I2=6
2. 12I1+13I2=10
162.5I1+156I2=78(Equation 3)
144I1+156I2=120(Equation 4)
(162.5I1−144I1)+(156I2−156I2)=78−120
18.5I1=−42
I1=−4218.5≈−2.27 A
- Substitute I1 back into Equation 2:
12(−2.27)+13I2=10
−27.24+13I2=10
13I2=37.24
I2≈2.86 A
- Current through Battery 1 (I1) = -2.27 A (indicating it flows in the opposite direction)
- Current through Battery 2 (I2) = 2.86 A
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:PRADEEPChapter:CURRENT ELECTRICITYExercise:Conceptual Problems
Explore 3 Videos
- CURRENT ELECTRICITYBook:PRADEEPChapter:CURRENT ELECTRICITYExercise:Very short Q/A
Explore 7 Videos
- COMMUNICATION SYSTEMSBook:PRADEEPChapter:COMMUNICATION SYSTEMSExercise:MODEL TEST PAPER-2
Explore 9 Videos
- DUAL NATURE OF RADIATION AND MATTERBook:PRADEEPChapter:DUAL NATURE OF RADIATION AND MATTERExercise:Exercise
Explore 191 Videos
Similar Questions
A battery of emf 6V internal resistance 5Ω is joined in parallel with another cell of emf of 10V and internal resistance 1Ω and the combination is used to send current through a resistor of 12Ω. Calculate the current through each battery.
View SolutionA battery of emf 6 volts and internal resistance 1Ω is connected in parallel to another battery of emf 8V and internal resistance 2Ω. The combination is then used to send current through an external resistance of 10Ω. Find the current through the external resistance.
View Solution
Knowledge Check
The internal resistance of a 2.1 V cell which gives a current of 0.2A through a resistance of 10Ω is
A0.5ΩB0.8ΩC1.0ΩD0.2ΩThe internal resistance of a 2.1V cell which gives a current 0.2A through a resistance of 10Ω
A0.2ΩB0.5ΩC0.8ΩD1.0Ω
Three batteries of emf 4,5 and 6V and internal resistances 1,2 and 3Ω respectively are connected in parallel with each other and the combination sends a current through an external resistance of 4Ω. Find current drawn through each battery.
View SolutionHow would you arrange 64 similar cells each having an emf of 2.0 V and internal resistance 2Ω so as to send maximum current through an external resistance of 8Ω.
View SolutionA battery of emf 3 V and internal resistance 1Ω is connected in parallel with a cell of emf 1.5 V and internal resistance 0.5Ω with their like poles together. The combination is used to pass a current through a resistor of resistance of 5Ω. Using Kirchhoffs circuital laws, find the current through the 5Ω resistor.
View SolutionA battery of emf 2V and internal resistance 0.5(Ω)is connected across a resistance in 1 second?
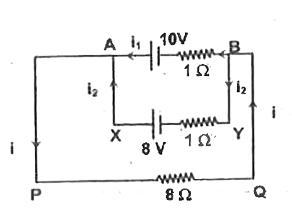
View SolutionTwo cells having emf's of 10 V and 8 V, and internal resistance of 1Ω(each) are connected as shown with an external resistance of 8Ω Find the current flowing through the circuit.
View SolutionA bulb of resistance 5Ω is connected to a battery of emf 4.2 V and internal resistance 1Ω. Find the current through the bulb.
View Solution

