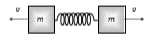
Two blocks each of mass m are connected to a spring of spring constant k. if both are given velocity v in opposite directions, then the maximum elongation of the spring is
√mv2k
√2mv2k
√mv22k
2√mv2k
The correct Answer is:B
Law of conservation of energy-
12mv2+12mv2=12kx2
⇒mv2=12kx2⇒x=√2mv2k.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - ERRORLESSCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - NCERT BASED QUESTIONS (Superposition of S.H.M.s and Resonance)
7 Videos
- SIMPLE HARMONIC MOTIONBOOK - ERRORLESSCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - PAST YEARS QUESTIONS
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - ERRORLESSCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - NCERT BASED QUESTIONS (Simple Pendulum)
27 Videos
- ROTATIONAL MOTIONBOOK - ERRORLESSCHAPTER - ROTATIONAL MOTIONEXERCISE - Assertion & Reason
25 Videos
- SURFACE TENSIONBOOK - ERRORLESSCHAPTER - SURFACE TENSIONEXERCISE - ASSERTION & REASON
11 Videos
Similar Questions
A block of mass m suspended from a spring of spring constant k. Find the amplitude of S.H.M.
View SolutionTwo blocks of masses m, and m, are connected to the ends of a spring of spring constant k. System is kept at rest on a frictionless horizontal floor with spring in its natural length. Both the blocks are pulled along opposite directions with forces of same magnitude F. Calculate maximum elongation of spring and distances travelled by the blocks during this motion.
View Solution
Knowledge Check
A block of mass m is connected to two indentical springs of spring constant k which are in turn connected to fixed supports as shown in the figure. Find the time period for small oscillations of the block.
 A2π√mkB2π√m2kC2π√2mkDπ√m2k
A2π√mkB2π√m2kC2π√2mkDπ√m2k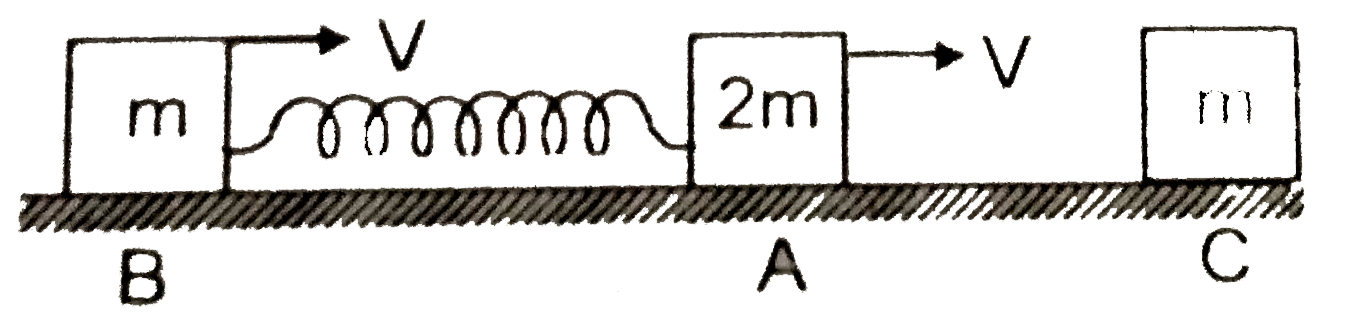
Two blocks A and B of mass 2 m and m respectively are connected to a massless spring of spring constant K. if A and B moving on the horizontal frictionless surface with velocity v to right. If A collides with C of mass m elastically and head on, then the maximum compressions of the spring will beA√32mkVB√27m8KVC√9m8KVD√8m27KVBlocks A&B of mass m each are connected with spring of constant k both blocks lie on frictionless ground and are imparted horizontal velocity v as shown when spring is unstretched find the maximum stretch of spring.
 Av√mkBv√m2kCv√2mkDnone
Av√mkBv√m2kCv√2mkDnone
2 mass of block 2 kg & 4 kg are attached to a stiffness spring 100 N/m. 2 kg mass is given velocity 2 m/s & 4 kg to 4 m/s in same direction. Find maximum elongation in the spring during the motion of two blocks.
View SolutionTwo blocks A and B each of mass m are connected by a massless spring of natural length L and spring constant k. The blocks are initially resting on a smooth horizontal floor with the spring at its natural length. A third identical block C also of mass m moves on the floor with a speed v along the line joining A and B and collides with A. Then
The kinetic energy of the A-B system at maximum compression of the spring is mv2/4
The maximum compression of the spring v√m/3k<br>Thek∈etice≠rgyoftheA−Bsystematmaxiμmcompression<br>Themaxiμmcoppressionofthespr∈gisvsqrt(m//k)
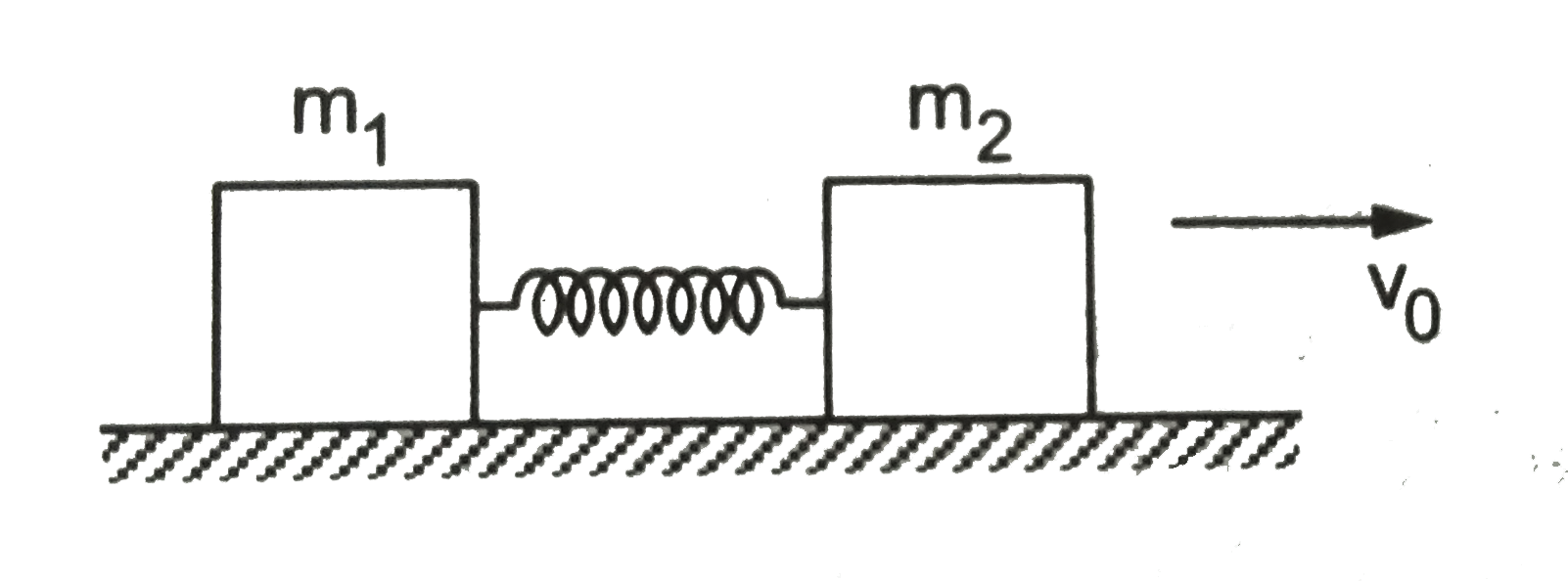
View SolutionTwo blocks of masses m1andm2 are connected by a spring of spring constant k figure. The block of mass m2 is given a shapr imulse so that it acquires a velocity v0 twoards right. Find a. the velocity of the cenre of mas b. the maximum elongation that teh spring will suffer.
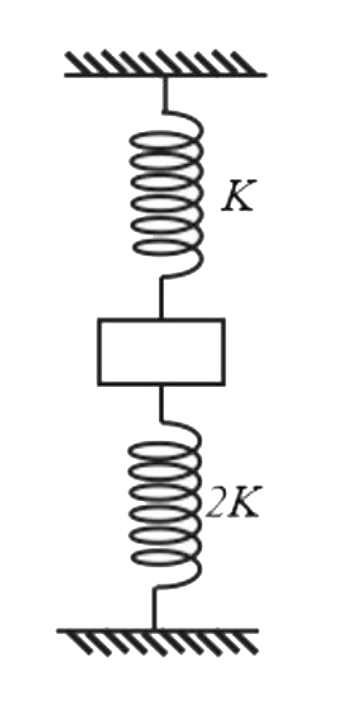
View SolutionA block of mass m is connected two springs of spring constant 2k annd k , respectively , as shown in the vertical plane. At equilibrium , both springs are compressed by same length. If suddenly lower spring is cut, then acceleration of block, just after spring cut , is
View SolutionA disc of mass m is connected with an ideal spring of stiffness k. If it is released from rest, it rolls without sliding on an inclination plane. The maximum elongation of the spring is:

View Solution
