An ideal spring with spring constant K = 200 N / m is fixed on one end on a wall. If the spring is pulled with a force 10 N at the other end along its length, how much it will extended
5 cm
2 m
2 cm
5 m
The correct Answer is:A
To solve the problem of how much the spring will extend when a force of 10 N is applied, we can use Hooke's Law, which states that the force exerted by a spring is proportional to its extension or compression. The formula for Hooke's Law is:
F=k⋅x
where:
- F is the force applied to the spring (in Newtons),
- k is the spring constant (in N/m),
- x is the extension of the spring (in meters).
1. Identify the Given Values:
- The spring constant k=200N/m
- The applied force F=10N
2. Apply Hooke's Law:
According to Hooke's Law, we can rearrange the formula to solve for x:
x=Fk
3. Substitute the Values:
Now, substitute the known values into the equation:
x=10N200N/m
4. Calculate the Extension:
Perform the calculation:
x=10200=0.05m
5. Convert to Centimeters:
Since the question may require the answer in centimeters, convert meters to centimeters:
x=0.05m×100cm/m=5cm
Final Answer:
The spring will extend by 5 centimeters when a force of 10 N is applied.
---
- F is the force applied to the spring (in Newtons),
- k is the spring constant (in N/m),
- x is the extension of the spring (in meters).
- The spring constant k=200N/m
- The applied force F=10N
According to Hooke's Law, we can rearrange the formula to solve for x:
x=Fk
Now, substitute the known values into the equation:
x=10N200N/m
Perform the calculation:
x=10200=0.05m
Since the question may require the answer in centimeters, convert meters to centimeters:
x=0.05m×100cm/m=5cm
The spring will extend by 5 centimeters when a force of 10 N is applied.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - ERRORLESSCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - NCERT BASED QUESTIONS (Superposition of S.H.M.s and Resonance)
7 Videos
- SIMPLE HARMONIC MOTIONBOOK - ERRORLESSCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - PAST YEARS QUESTIONS
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - ERRORLESSCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - NCERT BASED QUESTIONS (Simple Pendulum)
27 Videos
- ROTATIONAL MOTIONBOOK - ERRORLESSCHAPTER - ROTATIONAL MOTIONEXERCISE - Assertion & Reason
25 Videos
- SURFACE TENSIONBOOK - ERRORLESSCHAPTER - SURFACE TENSIONEXERCISE - ASSERTION & REASON
11 Videos
Similar Questions
Knowledge Check
An ideal spring with spring - constant K is bung from the colling and a block of mass M is attached to its lower end the mass is released with the spring initally unstetched . Then the maximum exlemsion in the spring is
A4MgKB2MgKCMgKDMg4KAn ideal spring with spring constant k is hung from the ceiling and a block of mass M is attached to its lower end. The mass is released with the spring initially unstretched. Then the maximum extension in the spring is
A(a) 4MgkB(b) 2MgkC(c) MgkD(d) Mg2k
One end of a fixed spring is pulled by an average force of 10N through a distance of 5cm, find the work done by the spring.
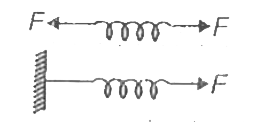
View SolutionFigure shows tow cases. In first case a spring (spring constant K) is pulled by two equal and opposite forces F at both ends and in second case is pulled by a force F at one end. Extensions (x) in the springs will be
View SolutionOne end of a light spring of spring constant k is fixed to a wall and the other end is tied to a block placed on a smooth horizontal surface. In a displacement, the work by the spring is 12kx2. The possible cases are
View SolutionA large fake cookie sliding on a horizontal surface is attached to one end of a horizontal spring with spring constant k=360 N/m, the other end of the spring is fixed in place. The cookie has a kinetic energy of 20.0 J as it passes through the spring's equilibrium position. As the cookie slides, a frictional force of magnitude 10.0 N acts on it . (a) How far will the cookie slide from the equilibrium position before coming momentarily to rest ? (c) What will be the kinetic energy of the cookie as it slides back through the equilibrium position ?
View SolutionA string of length 40 cm and weighing 10 g is attached to a spring at one end and to a fixed wall at the other end. The spring has a spring constant of 160Nm−1 and is stretched by 1-0 cm. If a wave pulse is produced on the string near the wall, how much time will it take to reach the spring ?
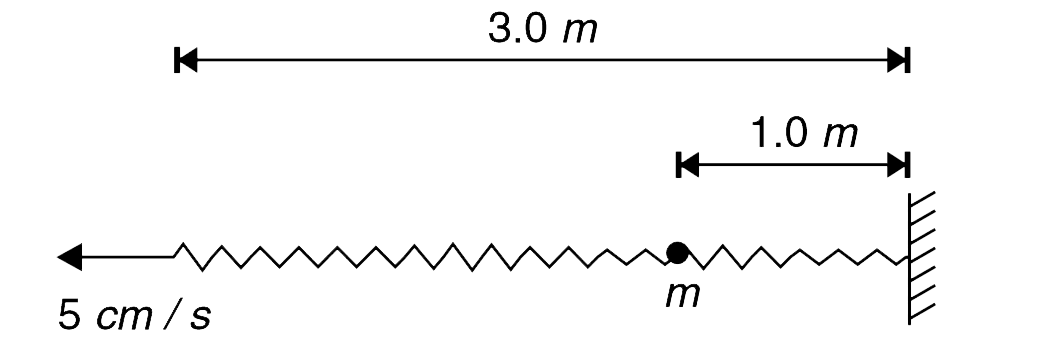
View SolutionA uniform light spring has unstretched length of 3.0 m. One of its end is fixed to a wall. A particle of mass m = 20 g is glued to the spring at a point 1.0 m away from its fixed end. The free end of the spring is pulled away from the wall at a constant speed of 5 cm/s. Assume that the spring remains horizontal (i.e., neglect gravity). Force constant of spring = 0.6 N / cm.
(a) With what speed does the particle of mass m move?
(b) Find the force applied by the external agent pulling the spring at time 2.0 s after he started pulling.
View Solution
