A block of mass 500 g is connected to a spring of spring constant k 312.5 N / m on a frictionless table. The spring is held firmly at the other end. The block is pulled a distance of 5 cm and then released to make SHM. Calculate the time period of its oscillations
2.0 s
1.75 s
0.5 s
0.25 s
The correct Answer is:D
To solve the problem of calculating the time period of oscillations for a block connected to a spring, we can follow these steps:
Step 1: Identify the given values
- Mass of the block (m) = 500 g = 0.5 kg (convert grams to kilograms)
- Spring constant (k) = 312.5 N/m
- Displacement (x) = 5 cm (not needed for time period calculation)
Step 2: Use the formula for the time period of a mass-spring system
The formula for the time period (T) of a mass-spring system undergoing simple harmonic motion is given by:
T=2π√mk
Step 3: Substitute the values into the formula
Now, substituting the values of mass (m) and spring constant (k) into the formula:
T=2π√0.5kg312.5N/m
Step 4: Calculate the value inside the square root
First, calculate the fraction:
0.5312.5=0.0016
Step 5: Calculate the square root
Now, take the square root of 0.0016:
√0.0016=0.04
Step 6: Multiply by 2π
Now, multiply by 2π:
T=2π×0.04≈0.2513seconds
Step 7: Round the answer
Rounding to two decimal places, we find:
T≈0.25seconds
Final Answer
The time period of the oscillations is approximately 0.25 seconds.
---
- Mass of the block (m) = 500 g = 0.5 kg (convert grams to kilograms)
- Spring constant (k) = 312.5 N/m
- Displacement (x) = 5 cm (not needed for time period calculation)
The formula for the time period (T) of a mass-spring system undergoing simple harmonic motion is given by:
Now, substituting the values of mass (m) and spring constant (k) into the formula:
First, calculate the fraction:
Now, take the square root of 0.0016:
Now, multiply by 2π:
Rounding to two decimal places, we find:
The time period of the oscillations is approximately 0.25 seconds.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - ERRORLESSCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - NCERT BASED QUESTIONS (Superposition of S.H.M.s and Resonance)
7 Videos
- SIMPLE HARMONIC MOTIONBOOK - ERRORLESSCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - PAST YEARS QUESTIONS
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - ERRORLESSCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - NCERT BASED QUESTIONS (Simple Pendulum)
27 Videos
- ROTATIONAL MOTIONBOOK - ERRORLESSCHAPTER - ROTATIONAL MOTIONEXERCISE - Assertion & Reason
25 Videos
- SURFACE TENSIONBOOK - ERRORLESSCHAPTER - SURFACE TENSIONEXERCISE - ASSERTION & REASON
11 Videos
Similar Questions
A block of mass m suspended from a spring of spring constant k. Find the amplitude of S.H.M.
View SolutionTwo blocks of masses m and m' are connected by a light spring on a horizontal frictionless table . The spring is compressed and then released . Find the ratio of acceleration of masses .
View Solution
Knowledge Check
Two masses m1 and m2 connected by a spring of spring constant k rest on a frictionless surface. If the masses are pulled apart and let go, the time period of oscillation is-
AT=2π√1k(m1m2m1+m2)BT=2π√1k(m1+m2m1m2)CT=2π√(m1k)DT=2π√(m2k)A block of mass m is connected to two indentical springs of spring constant k which are in turn connected to fixed supports as shown in the figure. Find the time period for small oscillations of the block.
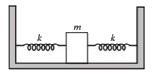 A2π√mkB2π√m2kC2π√2mkDπ√m2k
A2π√mkB2π√m2kC2π√2mkDπ√m2kA body of mass m is suspended from vertical spring and is set into simple harmonic oscillations of time period T. Next the spring is fixed at one end on a smooth horizontal table and same body is attached at the other end. The body is pulled slightly and then released to produce horizontal oscillations of the spring. The time period of horizontal oscillations is
ATB2TCT2DInfinite as the spring does not oscillate
A block of mass 100g attached to a spring ofstiffness 100N/Mis lying on a frictionless floor as shown. The block is moved to compress the spring by 10cm and released. If the collation with the wall is elastic then find the time period of oscillations.

View SolutionTwo blocks of masses m, and m, are connected to the ends of a spring of spring constant k. System is kept at rest on a frictionless horizontal floor with spring in its natural length. Both the blocks are pulled along opposite directions with forces of same magnitude F. Calculate maximum elongation of spring and distances travelled by the blocks during this motion.
View SolutionA block of mass m is connected to another .block of mass M by a massless spring of spring constant k. A constant force f starts action as shown in figure, then:

View SolutionSprings of spring constant k, 2k, 4k , 8k, …. Are connected in series. A block of mass 50 kg is attached to the lower end of the last spring and the system is set into oscillation. If k = 3.0 N/cm, what is the time period of oscillations ?
View SolutionA block of mass m is attached to a spring of force constant k whose other end is fixed to a horizontal surface. Initially the spring is in its natural length and the block is released from rest. The average force acting on the surface by the spring till the instant when the block has zero acceleration for the first time is
View Solution
