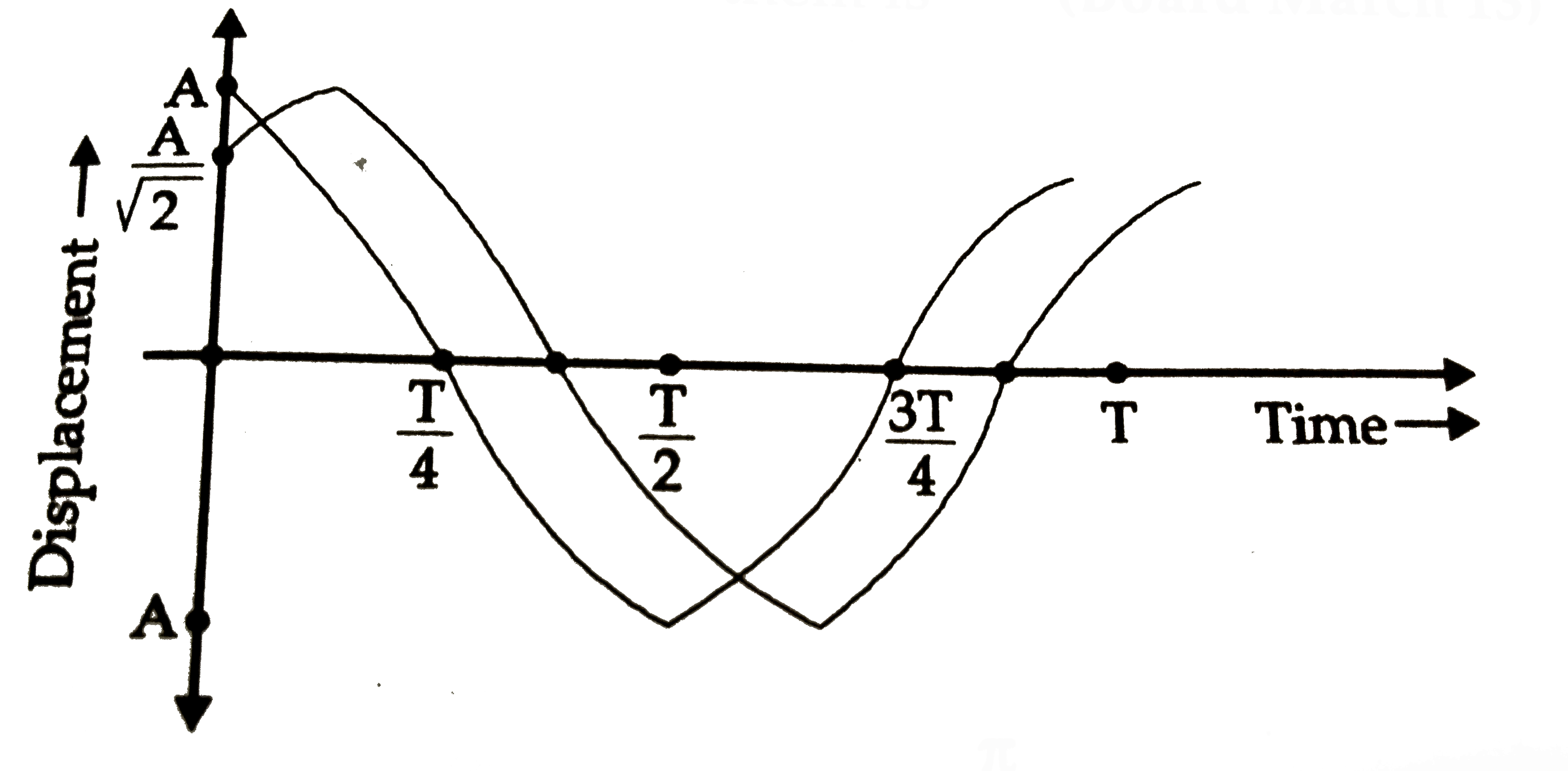
Two particles A and B execute simple harmonic motions of period T and $5 T / 4$ . They start from mean position. The phase difference between them when the particle A complete an oscillation will be

$π / 2$

$0$

$2 π / 5$

$π / 4$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Updated on:21/07/2023

Two particles A and B execute simple harmonic motions of period T and $5 T / 4$ . They start from mean position. The phase difference between them when the particle A complete an oscillation will be
A $π / 2$
Bzero
C $2 π / 5$
D $π / 4$
Two pendulums have time period T and 5T/4. They starts SHM at the same time from the mean position. What will be the phase difference between them after the bigger pendulum completed one oscillation ?
A $45^{\circ}$
B $90^{\circ}$
C $60^{\circ}$
D $30^{\circ}$
The phase difference between displacement and acceleration of a particle performing S.H.M. is
A $2 π$ rad
B $\frac{π}{2}$ rad
C $π$ rad
D $\frac{π}{4}$ rad