A uniform meter scale is put on a knife edge at 40 cm mark. It is found that this scale gets balanced when a weight of 20 gf is suspended from the 20 cm mark. Find the weight of meter scale.
To solve the problem, we need to analyze the forces acting on the meter scale and apply the principle of moments (torque). Here’s a step-by-step solution:
Step 1: Identify the system
We have a uniform meter scale (1 meter long) balanced on a knife edge at the 40 cm mark. The center of mass of the meter scale is located at the 50 cm mark.
Step 2: Define the forces
Let:
- m = weight of the meter scale (in gf)
- A weight of 20 gf is suspended from the 20 cm mark.
Step 3: Determine the moments
For the scale to be balanced, the clockwise moments must equal the anticlockwise moments about the fulcrum (the knife edge at the 40 cm mark).
1. Moment due to the 20 gf weight:
- Distance from the fulcrum (40 cm) to the 20 cm mark = 40cm−20cm=20cm
- Moment = Force × Distance = 20gf×20cm=400gf cm (anticlockwise)
2. Moment due to the weight of the meter scale:
- The weight m acts at the center of the scale, which is at the 50 cm mark.
- Distance from the fulcrum (40 cm) to the 50 cm mark = 50cm−40cm=10cm
- Moment = Force × Distance = m×10cm (clockwise)
Step 4: Set the moments equal
For the scale to be balanced:
Moment due to 20 gf=Moment due to weight of scale
400gf cm=m×10cm
Step 5: Solve for m
Rearranging the equation:
m=400gf cm10cm=40gf
Conclusion
The weight of the meter scale is 40gf.
---
We have a uniform meter scale (1 meter long) balanced on a knife edge at the 40 cm mark. The center of mass of the meter scale is located at the 50 cm mark.
Let:
- m = weight of the meter scale (in gf)
- A weight of 20 gf is suspended from the 20 cm mark.
For the scale to be balanced, the clockwise moments must equal the anticlockwise moments about the fulcrum (the knife edge at the 40 cm mark).
- Distance from the fulcrum (40 cm) to the 20 cm mark = 40cm−20cm=20cm
- Moment = Force × Distance = 20gf×20cm=400gf cm (anticlockwise)
- The weight m acts at the center of the scale, which is at the 50 cm mark.
- Distance from the fulcrum (40 cm) to the 50 cm mark = 50cm−40cm=10cm
- Moment = Force × Distance = m×10cm (clockwise)
For the scale to be balanced:
Moment due to 20 gf=Moment due to weight of scale
400gf cm=m×10cm
Rearranging the equation:
m=400gf cm10cm=40gf
The weight of the meter scale is 40gf.
Topper's Solved these Questions
- SAMPLE QUESTION PAPER 5 Book:ICSEChapter:SAMPLE QUESTION PAPER 5 Exercise:SECTION B
Explore 45 Videos
- SAMPLE QUESTION PAPER 4 Book:ICSEChapter:SAMPLE QUESTION PAPER 4 Exercise:SECTION B
Explore 38 Videos
- SELF ASSESSMENT PAPER -1Book:ICSEChapter:SELF ASSESSMENT PAPER -1Exercise:SECTION .B.
Explore 36 Videos
Similar Questions
A uniform half metre rule balances horizontally on a knife edge at 29 cm mark when a weight of 20 gf is suspended from one end.
What is the weight of the half metre rule ?
View SolutionA uniform half metre rule balances horizontally on a knife edge at 29 cm mark when a weight of 20 gf is suspended from one end.
Draw a diagram of the arrangement.
View Solution
Knowledge Check
Find the weight of half meter scale balanced at 5 cm mark when a weight of 10 gf is suspended at one of its ends.
A2.5gfB100gfC0.2gfD50gf
A uniform metre scale can be balanced at the 70.0 cm mark when a mass of 0.05 kg is hung from the 94.0 cm mark.
Find the mass of the metre scale.
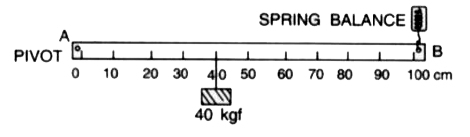
View Solutionbelow shows a uniform metre rule AB pivoted at its end A at the zero mark and supported at the other end B by a spring balance when a weight of 40kgf is suspended at its 40cm mark. This rule stays horizontal . Find the reading of the spring balance when the rule is of (i) negligible mass (ii) mass 20kg.
View SolutionA uniform metre rule between horizontally on a knife edge placed at the 58cm mark when a weight of 20gf is suspended from one end.
(i) Draw a diagram of the arrangement.
(ii) What is the weight of the rule?
View SolutionA uniform metre scale can be balanced at the 70.0 cm mark when a mass of 0.05 kg is hung from the 94.0 cm mark.
Draw a diagram of the arrangement.
View SolutionA uniform meter scale of mass 1kg is placed on table such that a part of the scale is beyond the edge. If a body of mass 0.25kg is hung at the end of the scale then the minimum length of scale that should lie on the table so that it does not tilt is
View SolutionA uniform metre rule rests horizontally on a knife edge at the 60cm mark when a mass of 10g is suspended from one end. Draw a diagram of the arrangement.
(a) At which end must this mass be suspended
(b) What is the mass of the rule?
(c ) THe 10g mass is now shifted to the 90cm mark. In which direction must the knife edge be shifted to make the rule horizontal again?
View SolutionThe diagram alongside shows a uniform metre rule of weight 100 gf being balanced on a knife edge placed at the 40 cm mark, by suspending a weight w gf at the mark 20 cm, find:
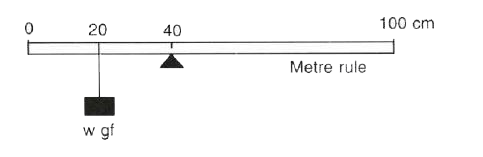
the position of another weight of 50 gf to balance the rule in part (ii).
View Solution