A rod of length l=2m is maintained to rotate with a constant angular velocity ω=1rad/s about vertical axis passing through one end (fig). There is a spring of spring constant k=1N/m which just encloses rod inside it in natural length. One end of the spring is attached to axis of rotation. S is sleeve of mass m=1kg which can just fir on rod. All surfaces are smooth. With what minimum kinetic energy (in J) sleeve should be projected so that it enters on the rod without impulse and completely compresses the spring.

The correct Answer is:6
For entering without jerk v2=lω0=2ms−1
Using work-energy theorem on the sleeve after entering in the frame of rod
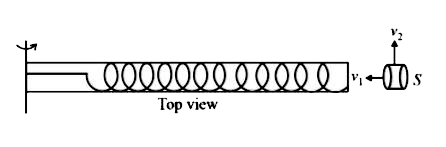
Wspring+Wcentrifugal=ΔK
−12kl2−12mω2l2=0−12m21
⇒v21=8
Now, K=12m(v21+v22)=6
Related Playlists
Knowledge Check
- Question 1 - Select One
A uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
A12mω2xB12mω2(1−x2l)C12mω2l(1−x2l2)D12mω2l[1−xl] - Question 1 - Select One or More
A thin uniform rod of mass m and length L rotates with the constant angular velocity ω about .the vertical axis passing through the rod's suspensjon point O. It describes a carried surface, then:
Acentrifugal force acting on rod is mL2sinθω2 and will pass through centre of massBcentrifugal force acting on rod is mL2sinθω2 and will not pass through centre of massCθ=cos−1(3g2ω2L)Dθ=cos−1(gω2L) - Question 1 - Select One
A thin uniform copper rod of length l and cross-section area A and mass m rotates uniformly with an angular velocity ω in a horizontal plane about a vertical axis passing through one of its ends. The elongation of the rod will be
Amω2l26AYBmω2l23AYCmω2l2AYDmω2l22AY - Question 1 - Select One
A uniform rod of mass m and length l is rotating with constant angular velocity ω about an axis which passes thorugh its one end and perpendicular to the length of rod. The area of cross section of the rod is A and its Young's modulus is y. Neglect gravity. The strain at the mid point of the rod is:
Amn2l8AyB3mω2l8AyC3mω2l4AyDmω4Ay - Question 1 - Select One
A uniform stick of length l and mass m lies on a smooth table. It rotates with angular velocity ω about an axis perpendicular to the table and through one end of the stick. The angular momentum of the stick about the end is
Aml2ωBml2ω3Cml2ω12Dml2ω6
Similar Questions
A rod of length l=2m is maintained to rotate with a constant angular velocity ω=1rad/s about vertical axis passing through one end (fig). There is a spring of spring constant k=1N/m which just encloses rod inside it in natural length. One end of the spring is attached to axis of rotation. S is sleeve of mass m=1kg which can just fix on rod. All surfaces are smooth. With what minimum kinetic energy (in J) sleeve should be projected so that it enters on the rod without impulse and completely compresses the spring.
 View Solution
View Solution
A rod of mass 2 kg ad length 2 m is rotating about its one end O wth an angular velocity ω=4rad/s. Find angular momentum of the rod about the axis rotation.View SolutionA thin uniform copper rod of length l and mass m rotates uniformly with an angular velocity ω in a horizontal plane about a vertical axis passing through one of its ends. Determine the tension in the rod as a function of the distance r from the rotation axis. Find the elongation of the rod.
View SolutionA uniform rod of mass m and length l0 is rotating with a constant angular speed ω about a vertical axis passing through its point of suspension. Find the moment of inertia of the rod about the axis of rotation if it make an angle θ to the vertical (axis of rotation).
View SolutionA metallic rod of length lis hinged at one end and the other end is rotated with a constant angular speed ω about an axis passing through the hinge. A constant and uniform magnetic field B, parallel to the axis of rotation exists everywhere. The induced emf between the two ends of rod is 12Blω2.
View Solution

