For a particle executing SHM, the kinetic energy (K) is given by K=K0cos2ωt. The equation for its displacement is
k0(mω2)1/2sinωt
(2k0mω2)1/2sinωt
(2ω2mk0)1/2sinωt
(2k0mω)1/2sinωt
The correct Answer is:B
If m is the mass, r is the amplitude of oscillation, then maximum kinetic energy,
k0=12mω2r2 or r=(2k0mω2)1/2
The displacement equation can be-
y=rsinωt=(2k0mω2)1/2sinωt
Topper's Solved these Questions
Similar Questions
If for a particle executing SHM, the equation of SHM is given as y=acosωt. Then which of the following graphs represents the variation in potential energy?
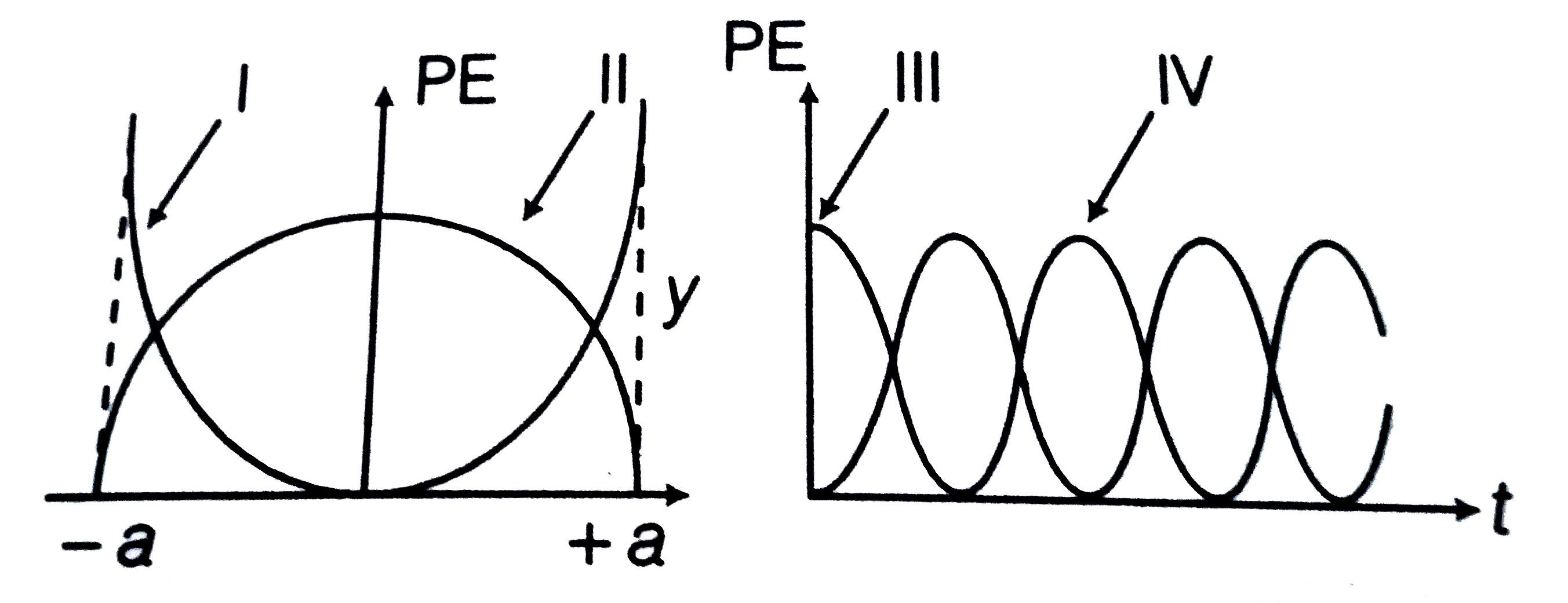
View SolutionFor a particle executing S.H.M. the displacement x is given by x=Acosωt . Identify the graph which represents the variation of potential energy (P.E.) as a function of time
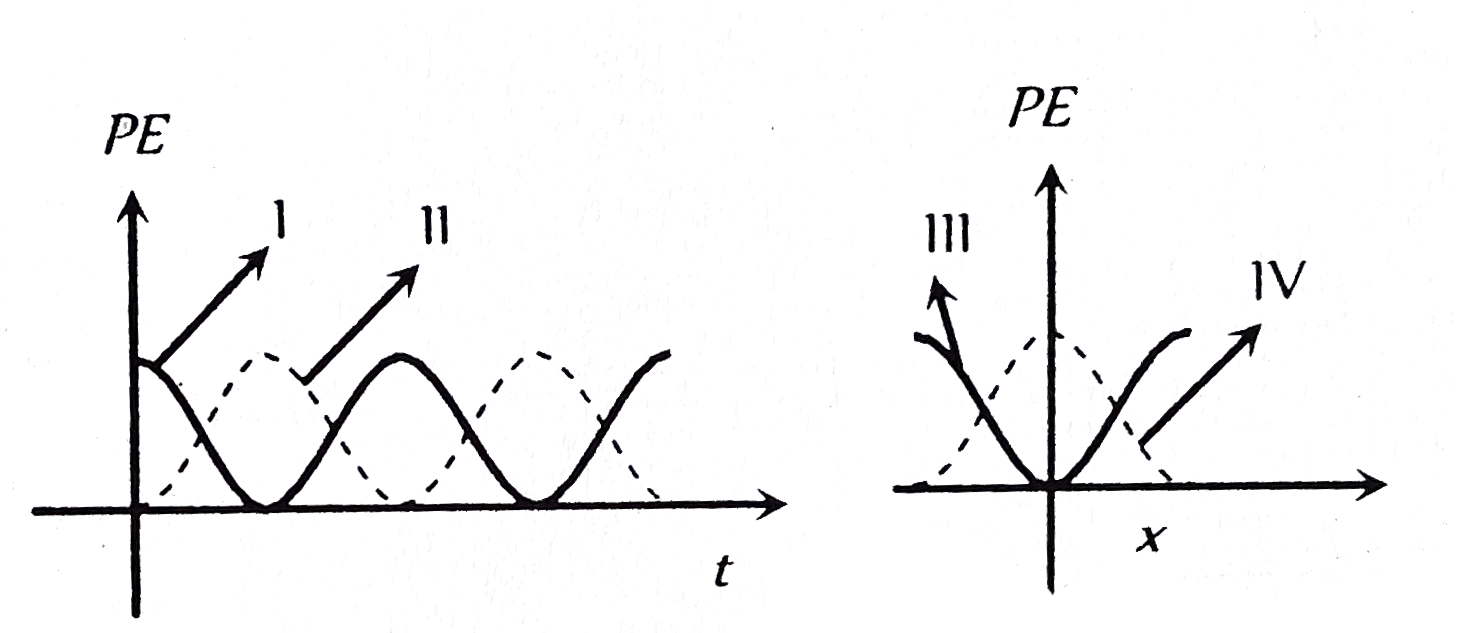
View Solution
Knowledge Check
For a particle executing S.H.M., the kinetic energy K is given K=K0cos2ωt. The maximum value of potential energy is:
AK0BzeroCK0/2Dnot abtainableThe displacement of a particle is given by x=cos2ωt. The motion is
Asimple harmonicBperiodic but not simple harmonicCperiodic but not simple harmonicDNone of the aboveFor a particle executing SHM along x-axis, force acting on it, is given by (A,k>0)
A−AkxBA cos kxCA exp (-kx)DAkx
The displacement of a particle executing simple harmonic motion is given by y=A0+Asinωt+Bcosωt. Then the amplitude of its oscillation is given by
View SolutionA particle executes SHM with an amplitude of 10cm and frequency 2Hz. At t=0, the particle is at a point where potential energy and kinetic energy are same. The equation for its displacement is
View SolutionThe particle executing simple harmonic motion has a kinetic energy K0cos2ωt. The maximum values of the potential energy and the total energy are respectively:
View SolutionThe total energy of a particle executing SHM is E. Its kinetic energy is K at the mean position. Then always
View SolutionThe particle executing simple harmonic motion has a kinetic energy K0cos2ωt. The maximum values of the potential energy and the energy are respectively
View Solution
