Find the thermal resistance of an aluminium rod of length 20cm and area of cross section 1cm2 . The heat current is along the length of the rod. Thermal conductivity of aluminium =200Wm−1K−1 .Solution in Gujrati
The thermalresistance is R=xKA=20×10−2m(200Wm−1K−1)(1×10−4m2)=10KW−1 .
Similar Questions
" A metal rod of area of cross section A has length L and coefficient of thermal conductivity K The thermal resistance of the rod is "
View SolutionThe dimensions of lKA are (l is the length of rod, K is the thermal conductivity of rod and A is the area of cross-section of rod)
View SolutionFind the thermal resistance of an aluminium rod of length 20cm and area of cross section 1cm2 . The heat current is along the length of the rod. Thermal conductivity of aluminium =200Wm−1K−1 .
View SolutionFind the rate of heat flow through a cross section of the rod shown in figure (θ2>θ1) . Thermal conductivity of the material of the rod is K.

View SolutionA rod of length 1 m having cross-sectional area 0.75m^(2) conducts heat at 6000Js^(-1) . Then the temperature difference acorss the rod is, if K=200Wm^(-1)K^(-1)
View SolutionThe ratio of the thermal conductivities of two different materials is 1 : 2 . The thermal resistance of the rods of these materials having the same thickness are equal. Find the ratio of the length of rods.
View SolutionThe temperature difference between the ends of a rod of aluminium of length 1.0 m and area of cross section 5.0 cm2 is 200∘C. How much heat will flow through the rod in 5 minutes ? The coefficient of thermal conductivity of aluminium is 0.2 kJ s−1 m−1 ∘C−1.
View Solution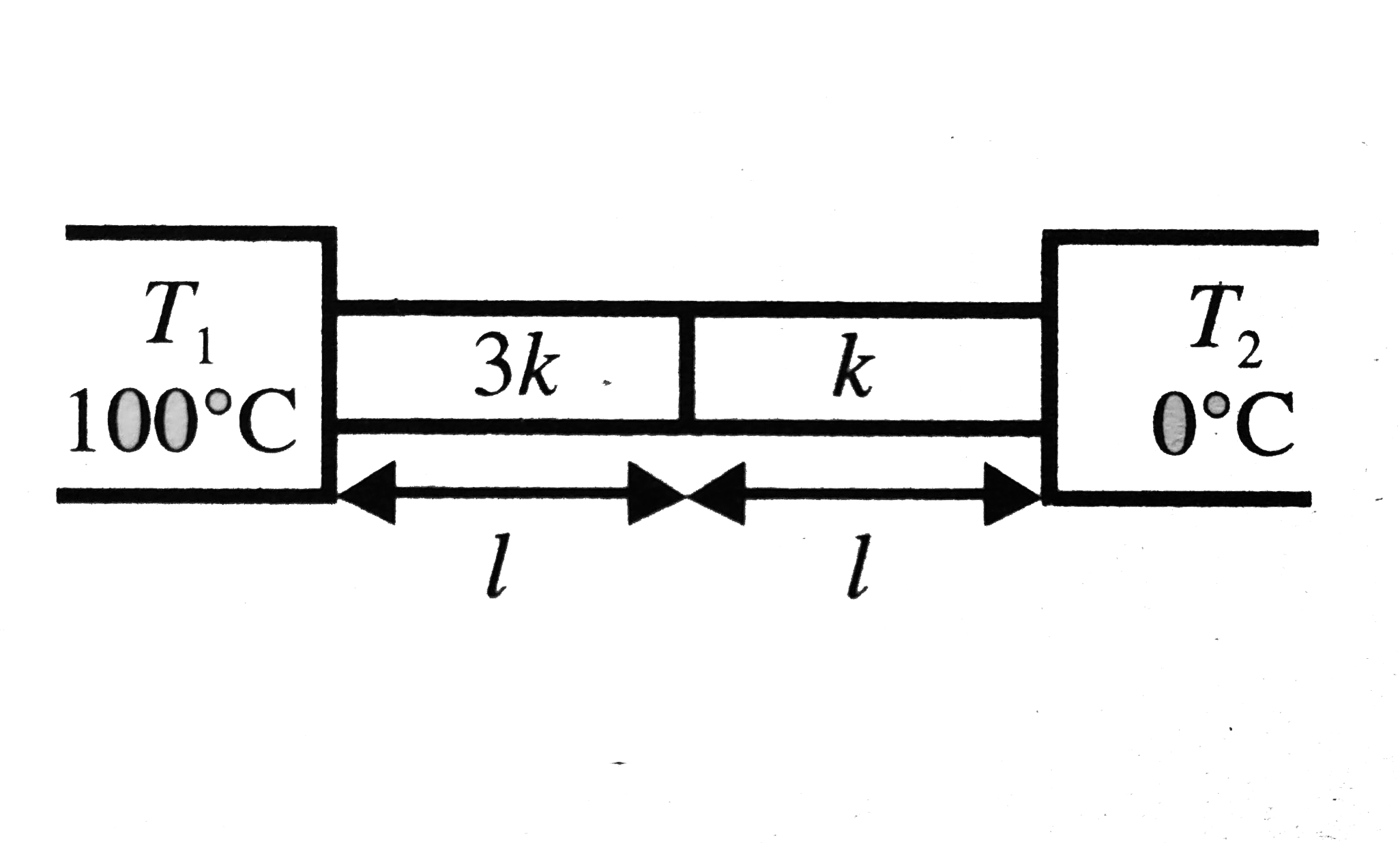
Two rods A and B of same length and cross-sectional area are connected in series and a temperature difference of 100∘C is maintained across the combination as shoen in Fig. If the thermal conductivity of the rod A is 3 k and that of rod B is k, Then
i.Determine the thermal resistance of each rod.
ii. determine the heat current flowing through each rod.
iii. determine the heat current flowing through each rod.
iv. plot the variation of temperature along the length of the rod.
View Solution