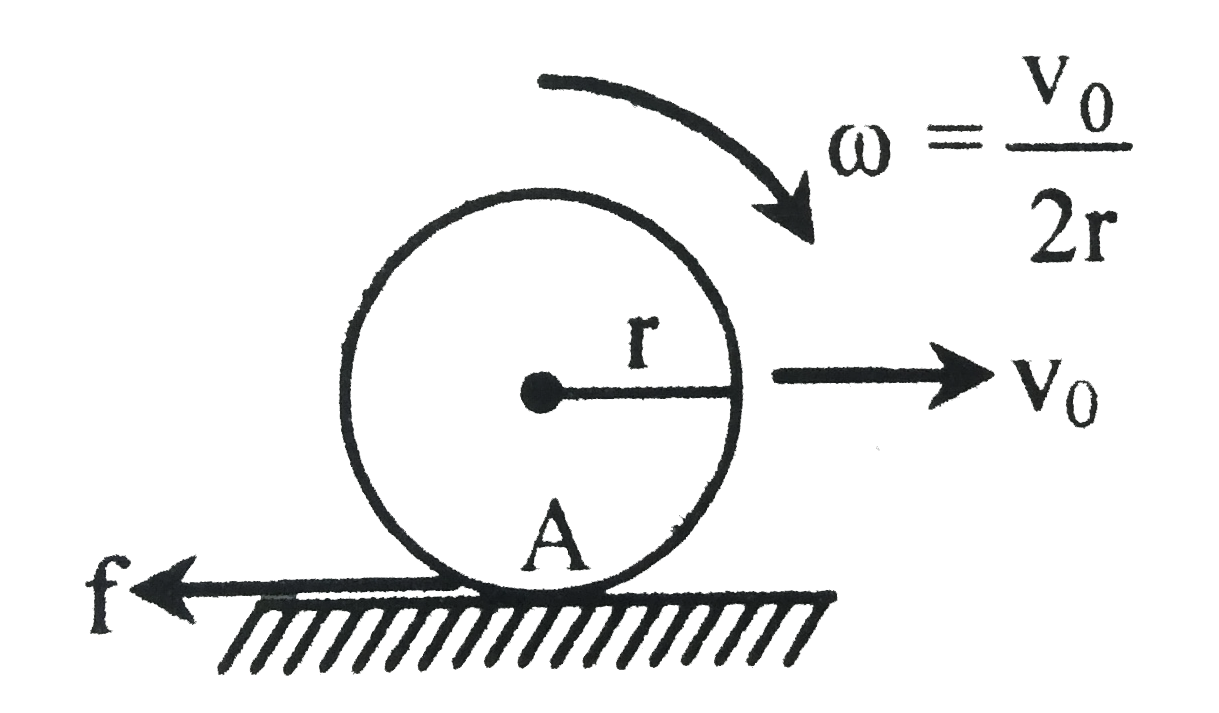
A sphere of mass M and radius r slips on a rough horizontal plane. At some instant it has translational velocity $V_{0}$ and rotational velocity about the centre $\frac{V_{0}}{2 r}$ . The translational velocity when the sphere starts pure rolling motion is Solution in Gujrati

Video Solution

Text Solution

Verified by Experts

Velociyt of the centre $= v_{0}$ and the angular velocity about the centre $= \frac{v_{0}}{2 r}$ . Thus $v_{0} > ω_{0} r .$ The sphre slips forward and thsu the friction by the plane on the sphere will act backward. As the friction is kinetic its value is $μ N = μ M g$ and the sphere will be decelerated by $a_{c m} = \frac{f}{M} .$ Hence
$v (t) = v_{0} - \frac{f}{M} t$ ............i
This friction will also have a torque $Γ =$ about the centre. This torque is clockwise and in the directionof $ω_{0}$ . Hence the angular acceleration about the centre will be
$a l p a = f \frac{r}{(\frac{2}{5}) (M r^{2}) = \frac{5 f}{2 M r}}$
and the clockwise angular velocity at time t will be
$ω (t) = \frac{5 f}{2 M r} t = \frac{v_{0}}{2 r} + \frac{5 f}{2 M r} t$
pure rolling starts when v(t)=romega(t) $< b r > i . e .$ v(t)=v_0/2+(5f)/(2M)t $... . i i < b r > e lim i \frac{N}{A} t \in t o m i and i i < b r >$ 5/2v(t)+v(t) =5/2 v_0+v_0/2 $< b r > or$ v(t)=2/7xx3v_=6/7v_0 $< b r > T h u s t h e s p h e r e r o l l s w i t h t r a n s l a t i o n v e l o c i t y$ 6v_0/7 $\in t h e f or w a r d d i r e c t i o n . < b r > A < e r \frac{N}{A} t i v e : \leq t u s c o n s r t h e \to r q u e b o u t t e h \in i t i l p \oint o f c o n t a c t A . T h e f or c e o f f i r c t i o n i p a s s e s t h r o u g h t h i s p \oint and h e c \neq i t s \to r q u e i s z e r ⊙ T h e n or j a l f or c e and t h e w e i g h t b a l a n c e e a c h o t h e r . T h e \neq t \to r q u e a b o u t A i s z e r ⊙ H e n c e t h e a n g a - - r m o m e n t u m a b o u t A i s c o n s e r v e d . < b r > I n i t i a l a n g a - - r o m e n t u m i s < b r >$ L=L_(cm)+Mrv_0+I_(cm)omega+Mrv_) $< b r >$ =(2/5Mr^2)(v_0)/(2r)+Mrv_0=6/5Mrv_0 $< b r > T h u s a n g a - - r v e l o c i t y i s$ v/r $. t h e a n g a - - r m o m e n t u m a b u t A i s < b r >$ L=L_(cm)+Mrv $< b r >$ =(2/5Mr^2)(v/r)+mrv+7/5Mrv $< b r > T h s u$ 6/5Mrv_0=7/5Mrv $< b r >$ or v=6/7v_0

Updated on:21/07/2023

|

Class 11 PHYSICS RIGID BODY DYNAMICS

Similar Questions

Recommended Questions

Home
Ask Doubt
Profile