A sphere of mass M and radius r slips on a rough horizontal plane. At some instant it has translational velocity V0 and rotational velocity about the centre V02r. The translational velocity when the sphere starts pure rolling motion is
V05
V07
V03
6V07
The correct Answer is:D
Step by step video, text & image solution for A sphere of mass M and radius r slips on a rough horizontal plane. At some instant it has translational velocity V_(0) and rotational velocity about the centre (V_(0))/(2r). The translational velocity when the sphere starts pure rolling motion is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TEST PAPERBook:ALLENChapter:TEST PAPERExercise:PHYSICS
Explore 4 Videos
- TEST PAPERBook:ALLENChapter:TEST PAPERExercise:PHYSICS
Explore 4 Videos
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Example
Explore 1 Video
- TEST PAPER 1Book:ALLENChapter:TEST PAPER 1Exercise:PHYSICS
Explore 11 Videos
Similar Questions
A solid sphere of mass M and radius r slips on a rough horizontal plane. At some instant it has translational velocity v0androtationalvelocityaboutthecentrev_(0) / 2 r.Thetranslationalvelocityafterthesphere⋆tspureroll∈gis(x v_(0))/(y)∈forwarddirection.F∈d(x+y).
'(##CEN_KSR_PHY_JEE_C09_E01_027_Q14##)'
View SolutionA sphere of mass M and radius r shown in figure slips on a rough horizontal plane. At some instant it has translational velocity V0 and rotational velocity about the centre v02r. Find the translational velocity after the sphere starts pure rolling.
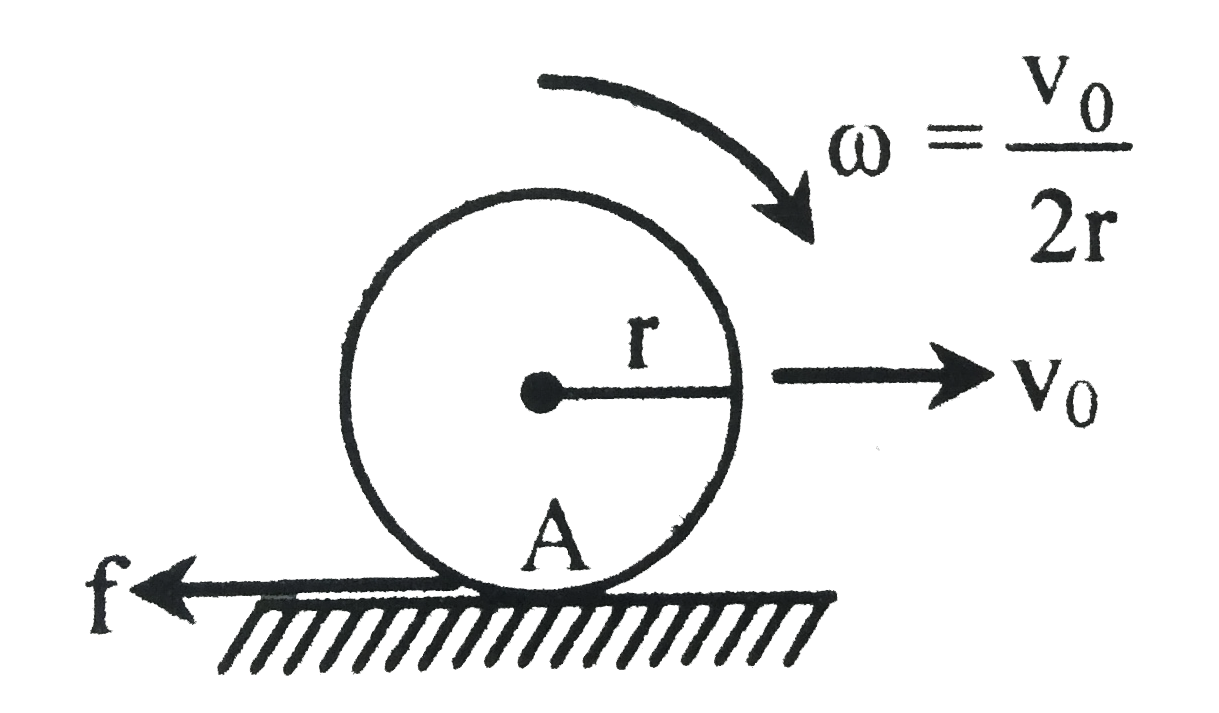 .
.
View Solution
Knowledge Check
A sphere of mass M and radius r shown in the figure on a rough horizontal plane. At some instant it has translational velocity v0, and rotational velocity about centre v0/2r. The percentage change of translational velocity after the sphere start pure rolling:
 A14.28%B7.14%C21.42%Dnone
A14.28%B7.14%C21.42%DnoneA ring of mass m and radius R is rolling on a horizontal plane. If the ring suddenly starts rotating about its diameter, then its angular velocity in this will be
AVRB2VRCV2RD√2VRA solid sphere of mass m and radius R rolls without slipping on a horizontal surface such that vc.m.=v0.
AThe kinetic energy of rotation is 15mv20.BThe total kinetic energy is 710mv20.CThe mechanical energy (assume the ground as reference) is mgR+710mv20.DAll options are correct.
A sphere of mass M and radius r shown in figure slips on a rough horizontal plane. At some instant it has translational velocity V0 and rotational velocity about the centre v02r. Find the translational velocity after the sphere starts pure rolling.
 .
.
View Solution(i) A solid sphere of radius R is released on a rough horizontal surface with its top point having thrice the velocity of its bottom point A (VA=V0) as shown in figure. Calculate the linear velocity of the centre of the sphere when it starts pure rolling.
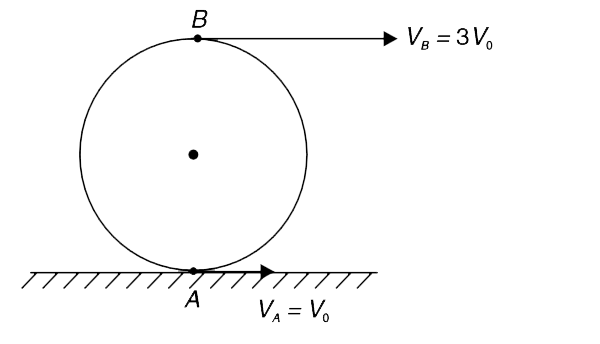
(ii) Solid sphere of radius R is placed on a rough horizontal surface with its centre having velocity V0 towards right and its angular velocity being ω0 (in anticlockwise sense). Find the required relationship between V0 and ω0 so that -
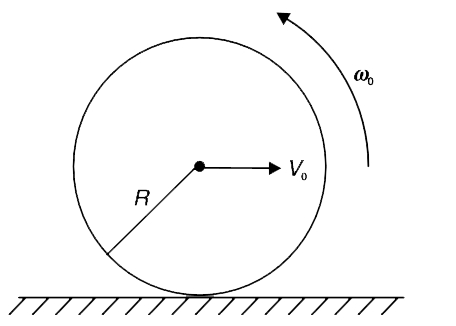
(a) the slipping ceases before the sphere loses all its linear momentum.
(b) the sphere comes to a permanent rest after some time.
(c) the velocity of centre becomes zero before the spinning ceases.
View SolutionA ring of mass m and radius R is placed on a rough horizontal surface (co-efficient of friction μ) with velocity of C.M.v0 and angular speed 2V0R as shown in figure. Initially the ring is rolling with slipping but attains pure rolling motion after some time t. Then
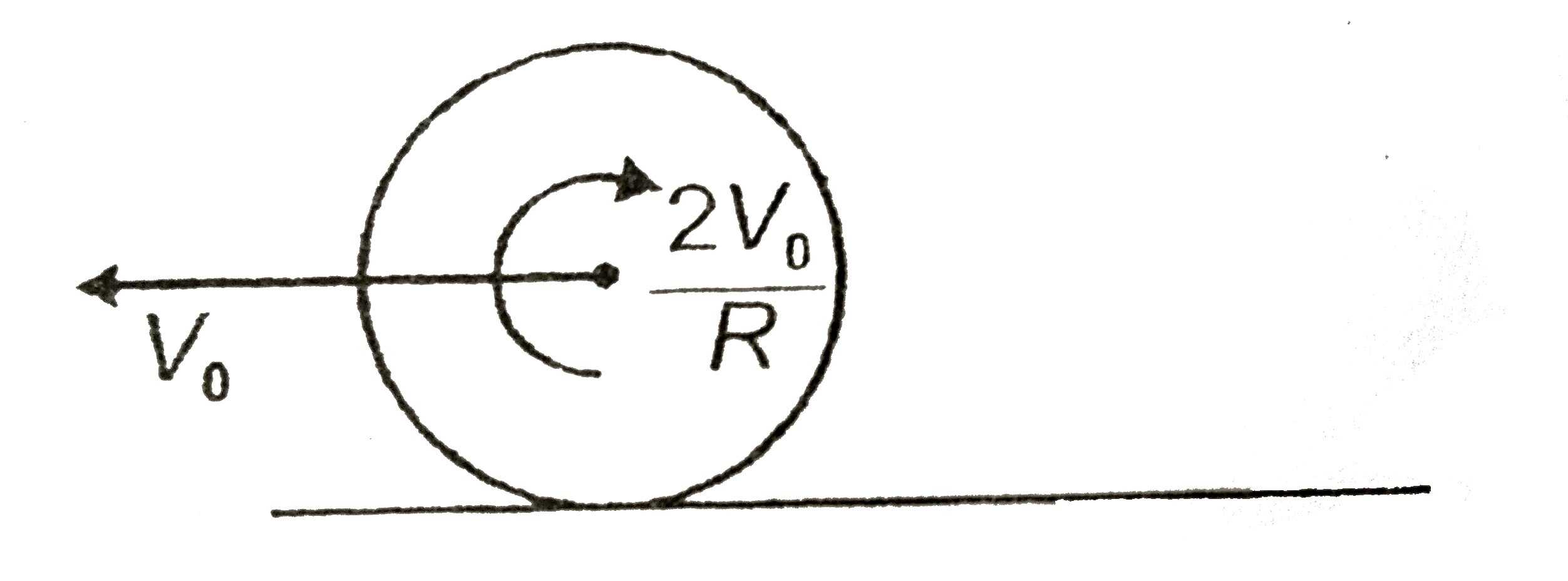
View SolutionA uniform solid sphere of mass m and radius r = 3m is projected along a rough horizontal surface with the initial velocity v0=6m/s and angular ω0 velocity as shown in the figure. If the sphere finally comes to complete rest then angular velocity is x rad/s. Find x.

View SolutionA solid homogeneous sphere is moving on a rough horizontal surface, partly rolling and partly sliding. During the king of motion of the sphere.
View Solution

