A sphere of mass m and radius R is kept on a rough floor. A sharp impulse is applied in the horizontal direction at the height of centre of sphere so that sphere acquires a linear velocity v0 without any angular velocity. Calculate the velocity of sphere when pure rolling starts.
To solve the problem, we need to analyze the motion of the sphere after the impulse is applied. The sphere starts with a linear velocity v0 and no angular velocity. We will find the velocity of the sphere when pure rolling starts.
1. Understanding the Initial Conditions:
- The sphere has a mass m and radius R.
- It is given a sharp impulse that imparts a linear velocity v0 without any initial angular velocity.
2. Identifying Forces and Motion:
- After the impulse, the sphere will experience friction with the rough surface.
- This friction will act in the opposite direction to the linear motion and will cause the sphere to start rotating.
3. Condition for Pure Rolling:
- Pure rolling occurs when the point of contact with the ground has zero velocity.
- This means that the linear velocity v of the center of mass and the angular velocity ω are related by the equation:
v=ωR
4. Applying the Conservation of Angular Momentum:
- We will calculate the angular momentum about the point of contact (point P) when the sphere starts rolling.
- The initial angular momentum Linitial about the center of mass is given by:
Linitial=mv0R
- The final angular momentum Lfinal when the sphere is rolling is given by:
Lfinal=Icmω+mvR
- Here, Icm=25mR2 is the moment of inertia of the sphere about its center of mass.
5. Setting Up the Equation:
- Since angular momentum is conserved, we have:
mv0R=mvR+25mR2ω
6. Substituting for Angular Velocity:
- Substitute ω=vR into the equation:
mv0R=mvR+25mR2(vR)
- Simplifying gives:
mv0R=mvR+25mvR
- Combine terms:
mv0R=mvR(1+25)=mvR(75)
7. Solving for v:
- Cancel m and R (assuming R≠0):
v0=75v
- Rearranging gives:
v=57v0
Final Result:
The velocity of the sphere when pure rolling starts is:
v=57v0
- The sphere has a mass m and radius R.
- It is given a sharp impulse that imparts a linear velocity v0 without any initial angular velocity.
- After the impulse, the sphere will experience friction with the rough surface.
- This friction will act in the opposite direction to the linear motion and will cause the sphere to start rotating.
- Pure rolling occurs when the point of contact with the ground has zero velocity.
- This means that the linear velocity v of the center of mass and the angular velocity ω are related by the equation:
v=ωR
- We will calculate the angular momentum about the point of contact (point P) when the sphere starts rolling.
- The initial angular momentum Linitial about the center of mass is given by:
Linitial=mv0R
- The final angular momentum Lfinal when the sphere is rolling is given by:
Lfinal=Icmω+mvR
- Here, Icm=25mR2 is the moment of inertia of the sphere about its center of mass.
- Since angular momentum is conserved, we have:
mv0R=mvR+25mR2ω
- Substitute ω=vR into the equation:
mv0R=mvR+25mR2(vR)
- Simplifying gives:
mv0R=mvR+25mvR
- Combine terms:
mv0R=mvR(1+25)=mvR(75)
- Cancel m and R (assuming R≠0):
v0=75v
- Rearranging gives:
v=57v0
The velocity of the sphere when pure rolling starts is:
v=57v0
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:MODERN PUBLICATIONChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:NCERT FILE ( NCERT TEXTBOOK EXERCISES )
Explore 21 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:MODERN PUBLICATIONChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:NCERT FILE ( NCERT (ADDITIONAL EXERCISES) )
Explore 12 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:MODERN PUBLICATIONChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:Conceptual Questions
Explore 24 Videos
- PHYSICAL WORLD Book:MODERN PUBLICATIONChapter:PHYSICAL WORLD Exercise:Revision exercises (Long answer questions)
Explore 6 Videos
- THERMAL PROPERTIES OF MATTERBook:MODERN PUBLICATIONChapter:THERMAL PROPERTIES OF MATTERExercise:CHAPTER PRACTICE TEST
Explore 15 Videos
Similar Questions
A uniform sphere of mass m and radius R is placed on a rough horizontal surface. The sphere is struck horizontally at a heighth from the floor. Match the following:

View SolutionA billiard ball of mass m and radius r, when hit in a horizontal direction by a cue at a height h above its centre, acquired a linear velocity v0. The angular velocity ω0 acquired by the ball is
View Solution
Knowledge Check
A billiard ball of mass m and radius 7, when hit in a horizontal direction by a cue at a height h above its centre, acquired a linear velocity v0. The angular velocity Wo acquired by the ball is
A5v0r22hB2v0r25hC2v0h5r2D5v0h2r2
A solid sphere of mass ma nd radis R is placed on a rough horizontal surface A horizontal force F is applied to sphere at a height h, (0≤h≤R) from centre. If sphere rolls slipping then,AThe maximum possible acceleration of sphere is FMBThe maximum possible acceleration of sphere is 10F7MCThe magnitude of friction force acting on the sphere is zero if h=2R5DThe magnitude of friction force acting on the sphere is zero h=3R4.A solid sphere of mass M and radius R is placed on a smooth horizontal surface. It is given a horizontal impulse J at a height h above the centre of mass and sphere starts rolling then, the value of h and speed of centre of mass are –
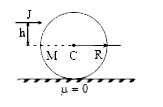 Ah=25Randv=JMBh=25Randv=25JMCh=75Randv=75JMDh=75Randv=JM
Ah=25Randv=JMBh=25Randv=25JMCh=75Randv=75JMDh=75Randv=JM
A unifrom sphere of mass m and radius R is placed on a rough horizontal surface (figure) .the sphere is stuuck horizontally at a height h from the floor . Match the following
View SolutionA uniform sphere of mass m and radius R is placed on a rough horizontal surface. The spher is struck horizontally at a height h from the floor. Show that the sphere rolls without slipping with a constant velocity, when h=7R/5.
View SolutionA sphere of mass m and radius R is kept on a rough horizontal floor. Constant force Facts at the top point of sphere along tangent. If there is sufficient friction on the floor to support pure rolling then calculate acceleration of sphere.
View SolutionA sphere of mass m and radius r is placed on a rough plank of mass M. The system is placed on a smooth horizontal surface. A constant force F is applied on the plank such that the sphere rolls purely on the plank. Find the acceleration of the sphere.

View SolutionA solid sphere of mass m and radius R rolls without slipping on a horizontal surface such that vc.m.=v0.
View Solution

