A sphere of mass m and radius R is kept on a rough horizontal floor. Constant force Facts at the top point of sphere along tangent. If there is sufficient friction on the floor to support pure rolling then calculate acceleration of sphere.
To solve the problem, we need to analyze the forces acting on the sphere and apply the concepts of rotational motion and pure rolling. Here’s a step-by-step solution:
Step 1: Identify the Forces Acting on the Sphere
The forces acting on the sphere are:
- The applied force F acting at the top of the sphere along the tangent.
- The frictional force f acting at the bottom of the sphere, opposing the motion.
- The weight of the sphere mg acting downwards at its center of mass.
- The normal force N acting upwards at the center of mass.
Step 2: Apply Newton’s Second Law for Translation
For the translational motion of the sphere, we can write:
F−f=ma
where a is the linear acceleration of the center of mass of the sphere.
Step 3: Apply Newton’s Second Law for Rotation
For the rotational motion about the center of mass, we can use the equation:
τ=Iα
where τ is the torque, I is the moment of inertia, and α is the angular acceleration. The torque due to the applied force F is:
τ=F⋅R
The moment of inertia I of a solid sphere about its center is:
I=25mR2
The angular acceleration α is related to the linear acceleration a by:
α=aR
Thus, we can write the torque equation as:
F⋅R−f⋅R=Iα
Substituting for I and α:
F⋅R−f⋅R=25mR2⋅aR
This simplifies to:
F−f=25ma(Equation 1)
Step 4: Combine the Equations
Now we have two equations:
1. F−f=ma (from translational motion)
2. F−f=25ma (from rotational motion)
We can set these equal to each other:
ma=25ma
This implies:
F−f=maandF−f=25ma
Step 5: Solve for Acceleration
From the equations, we can express f in terms of F and a:
f=F−ma(from translational motion)
Substituting f into the rotational equation:
F−(F−ma)=25ma
This simplifies to:
ma=25ma+f
Now, we can add both equations:
F=ma+f
Substituting f from the first equation:
F=ma+(F−ma)
This leads to:
F=75ma
Thus, solving for a:
a=5F7m
Final Answer
The acceleration of the sphere is:
a=5F7m
The forces acting on the sphere are:
- The applied force F acting at the top of the sphere along the tangent.
- The frictional force f acting at the bottom of the sphere, opposing the motion.
- The weight of the sphere mg acting downwards at its center of mass.
- The normal force N acting upwards at the center of mass.
For the translational motion of the sphere, we can write:
F−f=ma
where a is the linear acceleration of the center of mass of the sphere.
For the rotational motion about the center of mass, we can use the equation:
τ=Iα
where τ is the torque, I is the moment of inertia, and α is the angular acceleration. The torque due to the applied force F is:
τ=F⋅R
The moment of inertia I of a solid sphere about its center is:
I=25mR2
The angular acceleration α is related to the linear acceleration a by:
α=aR
Thus, we can write the torque equation as:
F⋅R−f⋅R=Iα
Substituting for I and α:
F⋅R−f⋅R=25mR2⋅aR
This simplifies to:
F−f=25ma(Equation 1)
Now we have two equations:
1. F−f=ma (from translational motion)
2. F−f=25ma (from rotational motion)
ma=25ma
This implies:
F−f=maandF−f=25ma
From the equations, we can express f in terms of F and a:
f=F−ma(from translational motion)
Substituting f into the rotational equation:
F−(F−ma)=25ma
This simplifies to:
ma=25ma+f
Now, we can add both equations:
F=ma+f
Substituting f from the first equation:
F=ma+(F−ma)
This leads to:
F=75ma
Thus, solving for a:
a=5F7m
The acceleration of the sphere is:
a=5F7m
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:MODERN PUBLICATIONChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:REVISION EXERCISES (Very Short Answer Questions Carrying 1 mark)
Explore 29 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:MODERN PUBLICATIONChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:REVISION EXERCISES (Additional Questions Carrying 1 mark )
Explore 4 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:MODERN PUBLICATIONChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:NCERT FILE (NCERT EXEMPLAR PROBLEMS (SUBJECTIVES QUESTIONS) (Very Short Answer Type Questions))
Explore 9 Videos
- PHYSICAL WORLD Book:MODERN PUBLICATIONChapter:PHYSICAL WORLD Exercise:Revision exercises (Long answer questions)
Explore 6 Videos
- THERMAL PROPERTIES OF MATTERBook:MODERN PUBLICATIONChapter:THERMAL PROPERTIES OF MATTERExercise:CHAPTER PRACTICE TEST
Explore 15 Videos
Similar Questions
A solid cylindrical roller of mass M and radius R is rolled on a rough horizontal surface by applying a horizontal force F at the top most point. The frictional force between the roller and the surface, is
View SolutionA sphere of mass m and radius r is placed on a rough plank of mass M. The system is placed on a smooth horizontal surface. A constant force F is applied on the plank such that the sphere rolls purely on the plank. Find the acceleration of the sphere.

View Solution
Knowledge Check

A uniform solid cylinder of mass m and radius R is placed on a rough horizontal surface. A horizontal constant force F is applied at the top point P of the cylinder so that it start pure rolling. The acceleration of the cylinder isAF/3mB2F/3mC4F/3mD5F/3m
A solid sphere of mass ma nd radis R is placed on a rough horizontal surface A horizontal force F is applied to sphere at a height h, (0≤h≤R) from centre. If sphere rolls slipping then,AThe maximum possible acceleration of sphere is FMBThe maximum possible acceleration of sphere is 10F7MCThe magnitude of friction force acting on the sphere is zero if h=2R5DThe magnitude of friction force acting on the sphere is zero h=3R4.A solid sphere of mass M and radius R is pulled horizontally on a rough surface as shown in Fig. Choose the incorrect alternatives.
 AThe magnitude of the frictional force isF/3.BThe frictional force on the sphere acts forward.CThe acceleration of the centre of mass is 2F/3MDThe acceleration of the centre of mass is F/M.
AThe magnitude of the frictional force isF/3.BThe frictional force on the sphere acts forward.CThe acceleration of the centre of mass is 2F/3MDThe acceleration of the centre of mass is F/M.
A uniform sphere of mass m and radius R is placed on a rough horizontal surface. The sphere is struck horizontally at a heighth from the floor. Match the following:

View SolutionA unifrom sphere of mass m and radius R is placed on a rough horizontal surface (figure) .the sphere is stuuck horizontally at a height h from the floor . Match the following
View SolutionA sphere of mass m and radius R is kept on a rough floor. A sharp impulse is applied in the horizontal direction at the height of centre of sphere so that sphere acquires a linear velocity v0 without any angular velocity. Calculate the velocity of sphere when pure rolling starts.
View SolutionA solid sphere of mass m and radius R is on a rough surface as shown in figure. Two forces having magnitude 2F and F are applied as shown. If the sphere perfors pure rolling along right direction, then frictional force acting on the sphere is
_PHY_211_Q01.png)
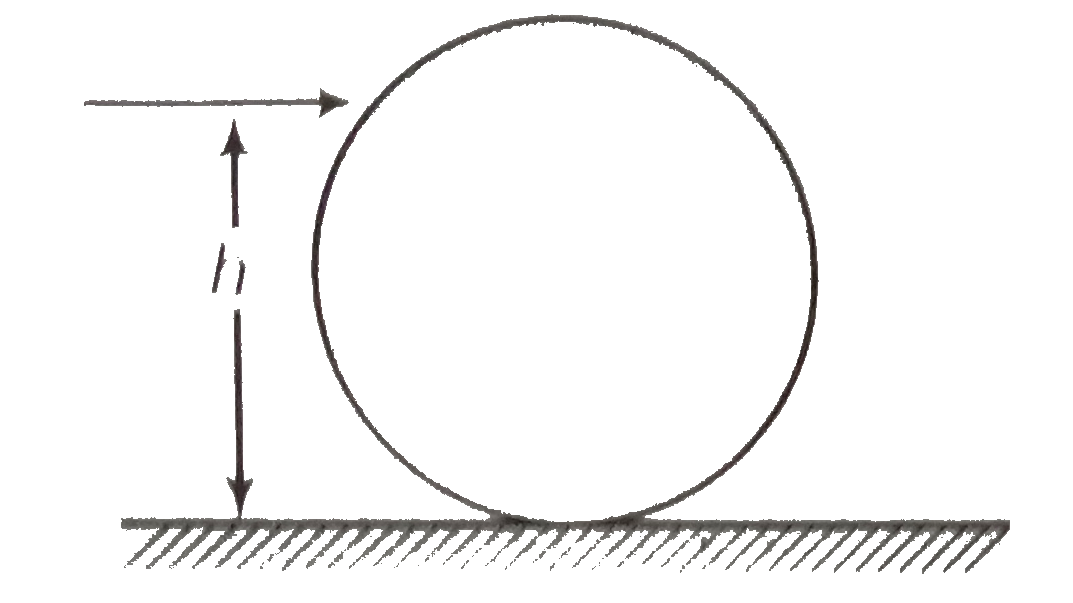
View SolutionSphere of mass M and radius R is kept on a rough horizontal floor. A small particle of mass m, moving horizontally with velocity, collides with the sphere and sticks to it. Line of motion of particle before collision is at a heighth above the floor. Assume that mase of sphere is very large in comparison to particle so that we may assume that centre of mass of the combined system remains at the centre of the sphere after the collision.
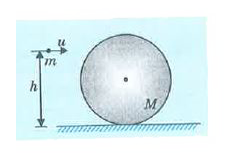
At what height h above the floor, particle should hit the sphere so that it may start pure rolling after the collision.
View Solution

