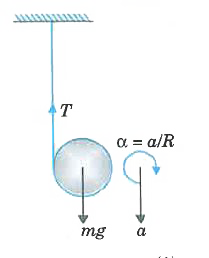
String is wrapped over a pulley and free end is fixed to the ceiling as shown in figure. Mass of the pulley is m and its radius is R. Assume that pulley is identical to dise. Calculate acceleration of pulley as it is allowed to fall by unwinding the string. Assume that string does not slip over the pulley.

Forces acting on the pulley are as shown in figure. Let a be the acceleration of the pulley and we know that string is not slipping over the pulley hence we can assume that angular acceleration. α=a/R
Using F - ma in the vertical direction we can write the following:
mg−T=ma ...(1)
Using τ=Iα about the centre of pulley we can write the following:
mg−ma2=ma⇒g=32a⇒a=2g3
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:MODERN PUBLICATIONChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:REVISION EXERCISES (Very Short Answer Questions Carrying 1 mark)
Explore 29 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:MODERN PUBLICATIONChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:REVISION EXERCISES (Additional Questions Carrying 1 mark )
Explore 4 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:MODERN PUBLICATIONChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:NCERT FILE (NCERT EXEMPLAR PROBLEMS (SUBJECTIVES QUESTIONS) (Very Short Answer Type Questions))
Explore 9 Videos
- PHYSICAL WORLD Book:MODERN PUBLICATIONChapter:PHYSICAL WORLD Exercise:Revision exercises (Long answer questions)
Explore 6 Videos
- THERMAL PROPERTIES OF MATTERBook:MODERN PUBLICATIONChapter:THERMAL PROPERTIES OF MATTERExercise:CHAPTER PRACTICE TEST
Explore 15 Videos
Similar Questions
Calculate the accelerations of the pulleys B and C and the tension in the string passing over the pulley A of the figure Figure 5.22.
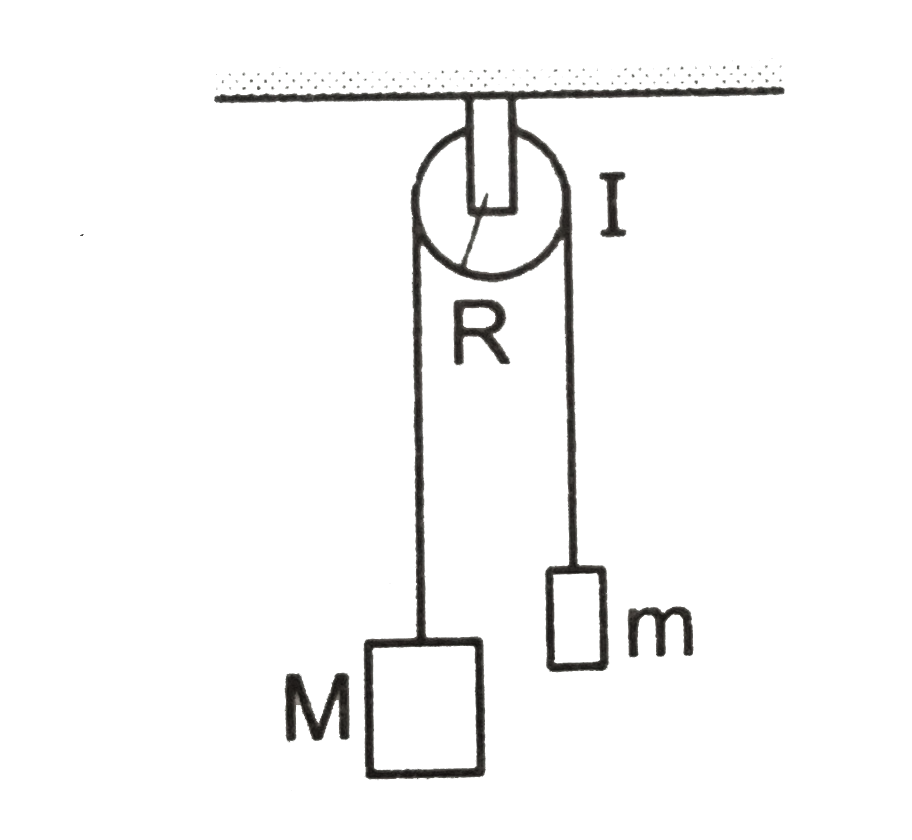
View SolutionThe pulley shown in figure has a moment of inertia I about it's axis and its radius is R. Find the magnitude of the acceleration of the two blocks. Assume that the string is light and does not slip on the pulley.
View Solution
Knowledge Check
A mas m hangs with help of a string wraped around a pulley on a frictionless bearling. The pulley has mass m and radius R. Assuming pulley to be a perfect uniform circular disc, the acceleration of the mass m, if the string does not slip on the pulley, is:
AgB23gCg3gD32gIf friction between pulley and string is sufficient to allow pure rolling then acceleration of pulley ‘A’ will be –
A2g7B4g5C4g7D2g3
Consider the situation shown in the figure. A mass is hanging from a inextensible string which is passing over a pulley. The pulley itself is attached to a massless spring of stiffness k as shown in the figure. Find the time period of vertical oscillations of mass m if pulley is slightly displaced from its mean position. Assume that string does not slip over pulley.
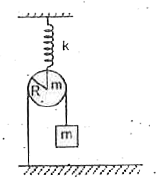
View SolutionSolve the previous problem if the pulley has a moment of inertia I about its axis and the string does not slip over it.
View SolutionConsider4 the situation shown in figure. Bothe the pulleys and the string are light and all the surfaces are friction less. a. Find the acceleration of the mass M. b. Find the tension in the string c. Calculate the force exerted by the clamp on the pulley A in the figure.

View SolutionConsider the situation shown in figure. Both the pulleys and the strings are light and all the surfaces are frictionless. Calculate
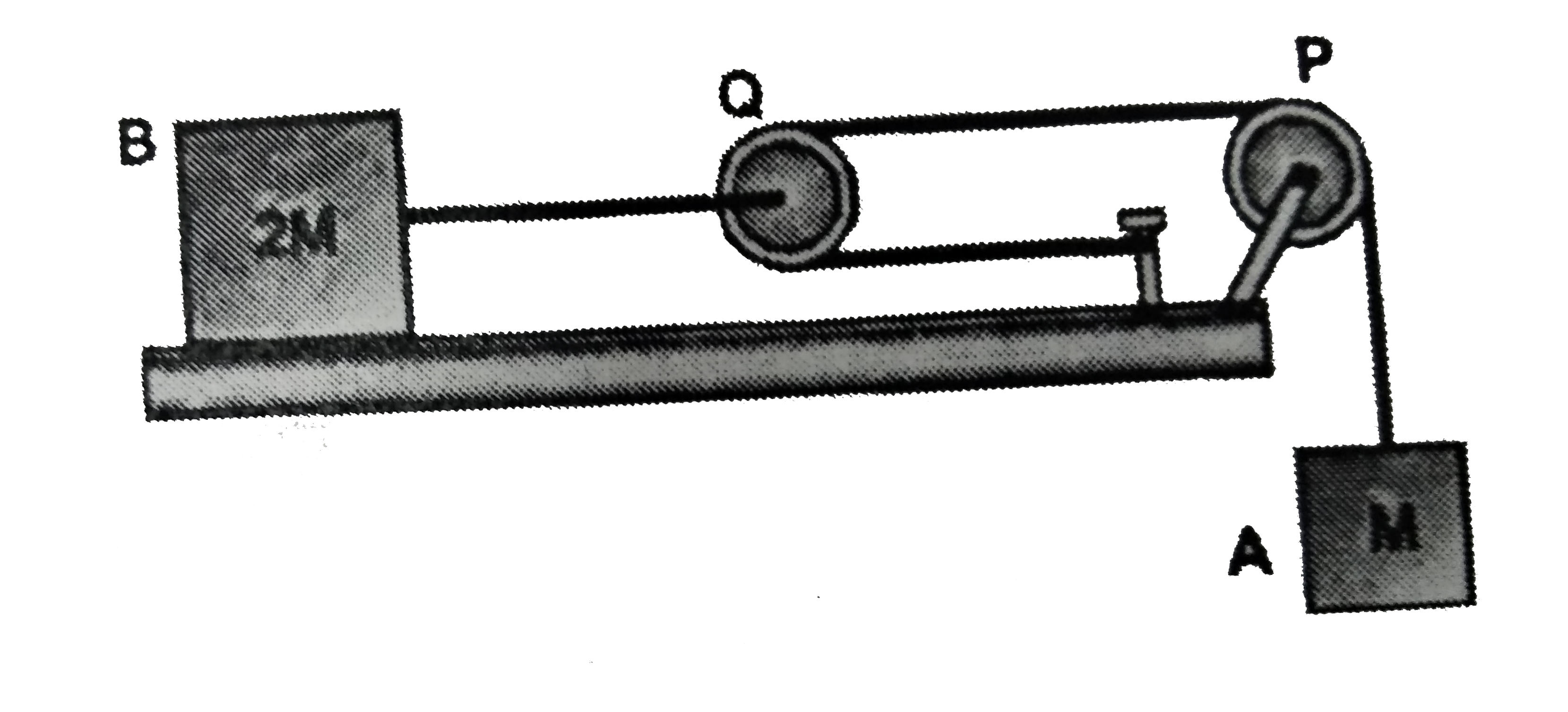
(a) the acceleration of mass M,
(b) tension in the string PQ and
(c ) force exerted by the pulley P.
View SolutionA string is wrapped over the edge a uniform disc and the free end is fixed with the ceiling. The disc moves down, unwinding the string. Find the downward acceleration of the disc.
View SolutionIn the pulley system shown the movable pulleys A,B and C have mass m each, D and E are fixed pulleys. The strings are vertical light and inextensible Then
 .
.
View Solution

