Question

Find the moment of inertia of a uniform ring of mass M and radius R about a diameter.

Explanation

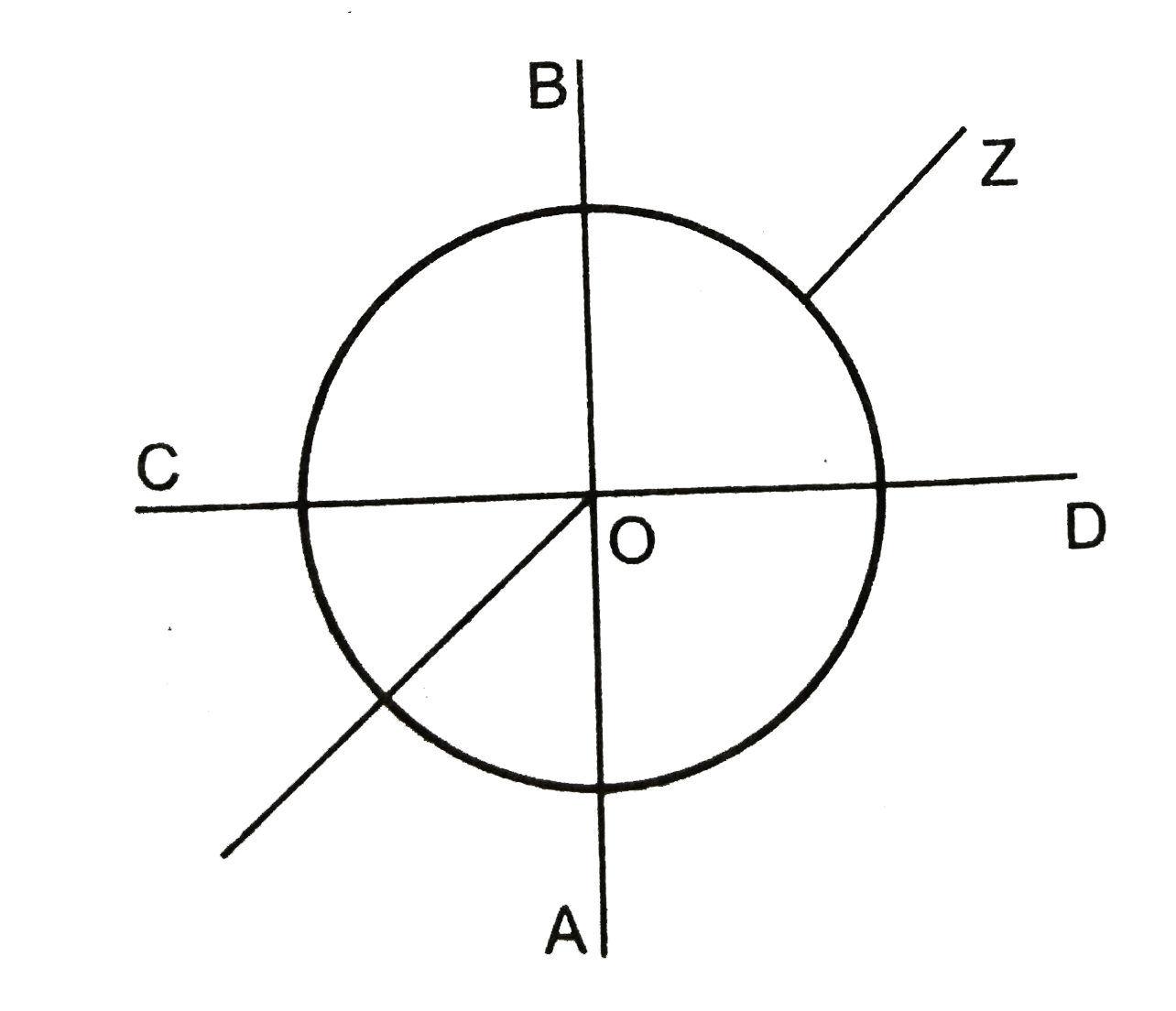
Let AB and CD be two mutually perpendicular diameter of the ring. Take them as M and Y axes and the line perpendicular to the plane of the ring through the centre as the Z-axis. The moment of inertia of the ring about the Z-axis is `I=MR^2`. As the ring is uniform, all of its diameters are equivalent and so `I_x=I_y`. From perpendicular axes theorem
`I_2=I_x+I_y Hence I_x=I_z/2=(MR^2)/2`.
Similarly the moment of inertia of a uniform disc about a diameter is a `MR^2/4`