Prove that moment of inertia of uniform ring of mass M and radius R about its geometric axis is MR2 Solution in Gujrati
Assume the dx is the element of length dx on the ring as shown in fig.
The mass per unit length of the ring.

λ=M2πR
∴ Mass of length dx is dx, m=λdx
∴m=M2πR.dx....(1)
∴ The moment of inertia about the axis ZZ.
dI=mR2
=M2πRR2dx
∴dI=MR2πdx
∴ For the moment of inertia along the whole ring take the integral from x=0 to x=2πR
∴I=∫dI
=2πR∫0M2πRdx=MR2π2πR∫0dx
=MR2π[x]2πR0=MR2π[2πR−0]
∴I=MR2
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:KUMAR PRAKASHANChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:SECTION-C OBJECTIVE QUESTIONS (VSQs)
Explore 52 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:KUMAR PRAKASHANChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:SECTION-D NCERT EXEMPLAR SOLUTIONS
Explore 13 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:KUMAR PRAKASHANChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:SECTION-B ADDITIONAL EXERCISE
Explore 12 Videos
- QUESTIONS ASKED IN JEE - 2020 Book:KUMAR PRAKASHANChapter:QUESTIONS ASKED IN JEE - 2020 Exercise:Question
Explore 16 Videos
- THERMAL PROPERTIES OF MATTERBook:KUMAR PRAKASHANChapter:THERMAL PROPERTIES OF MATTERExercise:Question Paper (Section - D) (Answer following in brief :) Each carry 4 marks
Explore 1 Video
Similar Questions
Give two examples of a rigid body where the center of mass lies outside in material of rigid body.
View SolutionFor which of the following does the centre of mass lie outside the body?
View SolutionThe longest wavelength in Balmer series of hydrogen spectrum will be
View SolutionA non-isotropic solid metal cube has coefficient of linear expansion as 5×10−5/∘C along the x-axis and 5×10−6/∘C along y-axis and z-axis. If the coefficient of volumetric expansion of the solid is n×10−6/∘C then the value of n is....
View SolutionIn an experiment on the specific heat of a metal, a 0.20 kg block of the metal at 150∘C is dropped in a copper calorimeter (of water equivalent 0.025 kg) containing 150 cm3 of water at 27∘C. The final temperature is 40∘C. Compute the specific heat of the metal. If heat losses to the surroundings are not negligible, is your answer greater or smaller than the actual value for specific heat of the metal ?
View SolutionMoment of inertia of a uniform circular ring of mass M and radius R about a diameter of ring is………………. .
View SolutionThe moment of inertia of a uniform circular ring, having a mass M and a radius R, about an axis tangential to the ring and perpendicular to its plane, is
View SolutionThe moment of inertia of a ring about its geometrical axis is I, then its moment of inertia about its diameter will be
View SolutionM द्रव्यमान और R त्रिज्या के एक ठोस बेलन का जड़त्व-आघूर्ण उसकी ज्यामितीय अक्ष के समान्तर और उसकी सतह पर स्थित अक्ष के परितः होगा :
View SolutionMoment of inertia of a cylindrical shell of mass M, radius R and length L about its geometrical axis would be -
View SolutionThe moment of inertia of a ring of mass M and radius R about PQ axis will be :-
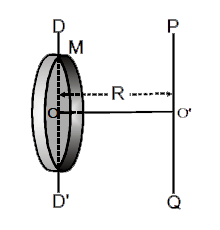
View SolutionThe moment of inertia of a ring of mass M and radius R about PQ axis will be
View SolutionMoment of inertia of a circular ring of mass m and radius r about the normal axis passing through its centre is
View SolutionFind the moment of inertia of a ring of mass m and radius r about an axis passing through the tangent to the circle of the ring.
View SolutionThe moment of inertia of a solid sphere of mass M and radius R, about an axis through its centre, is 25MR2. The moment of inertia about an axis tangential to the surface of the sphere will be :
View Solution

