In a meter bridge 30Ω resistance is connected in the left gap and a pair of resistance 20Ω and Q in (Ohm) are in right gap and they are connected in series, then the balanceing length is 50 cm. When they were connected in parallel the balanceing length will be
20 cm
40 cm
60 cm
81.81 cm
The correct Answer is:D
To solve the problem step by step, we will follow the process outlined in the video transcript while ensuring clarity and thoroughness.
Step 1: Understand the Setup
We have a meter bridge with:
- A 30 Ω resistor in the left gap.
- A combination of a 20 Ω resistor and an unknown resistor Q in series in the right gap.
- The balancing length is given as 50 cm.
Step 2: Use the Balancing Condition
The balancing condition for a meter bridge states that the ratio of the resistances is equal to the ratio of the lengths. Therefore, we can write:
R1L1=R2L2
where R1=30Ω, L1=50cm, R2=20+QΩ, and L2=100−50=50cm.
Substituting the values, we have:
3050=20+Q50
Step 3: Simplify the Equation
Cross-multiplying gives:
30×50=(20+Q)×50
This simplifies to:
30=20+Q
Step 4: Solve for Q
Rearranging the equation gives:
Q=30−20=10Ω
Step 5: Calculate the Equivalent Resistance in Parallel
Now, we need to find the equivalent resistance when the 20 Ω and 10 Ω resistors are connected in parallel. The formula for two resistors in parallel is:
1Req=1R1+1R2
Substituting the values:
1Req=120+110
Finding a common denominator (which is 20):
1Req=120+220=320
Thus,
Req=203Ω
Step 6: Set Up the New Balancing Condition
Now, we set up the balancing condition again with the new equivalent resistance:
30x=20/3100−x
where x is the new balancing length.
Step 7: Cross-Multiply and Solve for x
Cross-multiplying gives:
30(100−x)=203x
Expanding this:
3000−30x=203x
Multiplying through by 3 to eliminate the fraction:
9000−90x=20x
Combining like terms:
9000=110x
Thus,
x=9000110=90011≈81.81cm
Conclusion
The new balancing length when the resistors are connected in parallel is approximately 81.81 cm.
---
We have a meter bridge with:
- A 30 Ω resistor in the left gap.
- A combination of a 20 Ω resistor and an unknown resistor Q in series in the right gap.
- The balancing length is given as 50 cm.
The balancing condition for a meter bridge states that the ratio of the resistances is equal to the ratio of the lengths. Therefore, we can write:
R1L1=R2L2
where R1=30Ω, L1=50cm, R2=20+QΩ, and L2=100−50=50cm.
3050=20+Q50
Cross-multiplying gives:
30×50=(20+Q)×50
This simplifies to:
30=20+Q
Rearranging the equation gives:
Q=30−20=10Ω
Now, we need to find the equivalent resistance when the 20 Ω and 10 Ω resistors are connected in parallel. The formula for two resistors in parallel is:
1Req=1R1+1R2
Substituting the values:
1Req=120+110
Finding a common denominator (which is 20):
1Req=120+220=320
Thus,
Req=203Ω
Now, we set up the balancing condition again with the new equivalent resistance:
30x=20/3100−x
where x is the new balancing length.
Cross-multiplying gives:
30(100−x)=203x
Expanding this:
3000−30x=203x
Multiplying through by 3 to eliminate the fraction:
9000−90x=20x
Combining like terms:
9000=110x
Thus,
x=9000110=90011≈81.81cm
The new balancing length when the resistors are connected in parallel is approximately 81.81 cm.
Topper's Solved these Questions
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MOVING CHANGES & MEGNETISM)
95 Videos
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MAGNETISM AND MATTER )
52 Videos
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (ELECTRIC POTENTIAL & CAPACITANCE )
143 Videos
- ALTERNATING CURRENTBOOK - AAKASH SERIESCHAPTER - ALTERNATING CURRENTEXERCISE - EXERCISE - III
24 Videos
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - LAW OF MOTION
128 Videos
Similar Questions
A 6Ω resistance is connected in the left gap of a meter bridge. In the second gap 3Ω and 6Ω are joined in parallel. The balance point of the bridge is at _______
View SolutionWhen a conducting wire is connected in the left gap and known resistance in the right gap, the balance length is 75cm. If the wire is cut into 3 equal parts and one part isconnected in the left gap, the balance length
View Solution
Knowledge Check
In a meter bridge experiment the ratio of left gap resistance to right gap resistance is 2:3 the balance point from is
A60cmB50cmC40cmD20cm
Resistance of 100Ω and 200Ω are connected in series with 220 V mains. When a voltmeter of 1000Ω resistance is connected in parallel to100Ω , then the reading of voltmeter is
View SolutionThe Total resistance when connected in series in 9Ω and when connected in parallel is 2Ω The value of two resistance are
View SolutionWhen un known resistance and a resistance of 4Ω are used in the left and right gaps of a meter bridge, the balance point is 50cm. the shift in the balance point if a 4Ω resistance is now connected parallel to the resistor in right gap ______
View SolutionIn a meter bridge experiment, resistances are connected as shown in figure. The balancing length l1=55cm. Now, an unknown resistance x is connected in series with P and the new balancing length is found to be 75 cm. What is the value of The value of 11x (in ohm)? (Given, P=4Ω)
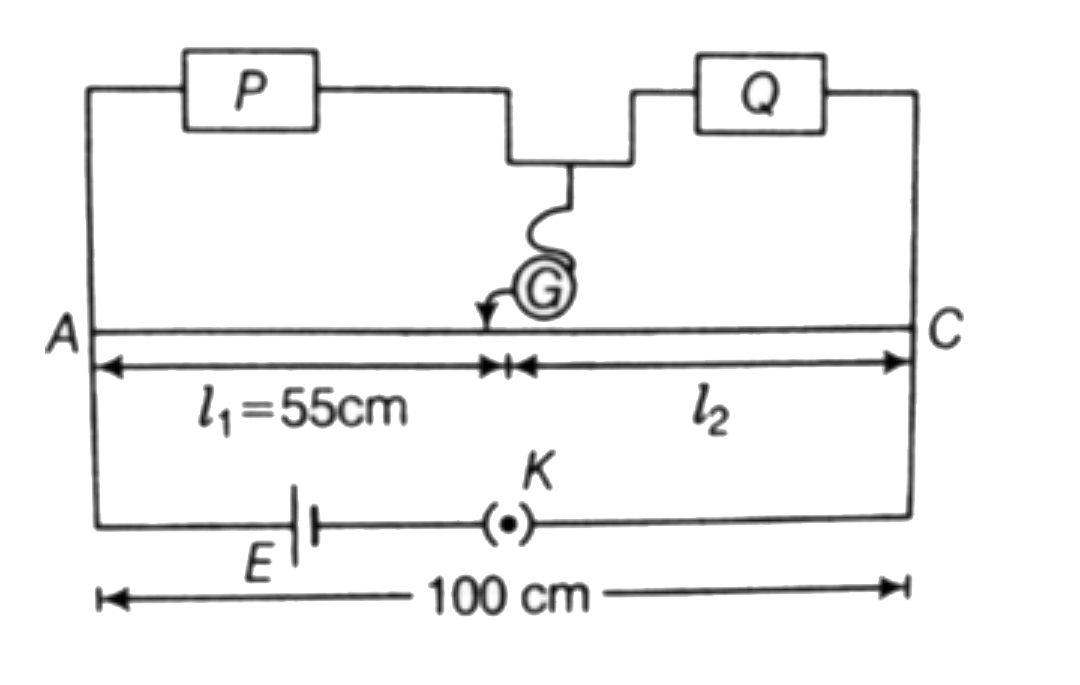
View SolutionIn metre bridge experiment, with a standard resistance in the right gap and a resistance coil dipped in water (in a beaker) in the left gap, the balancing length obtained is '1'. If the temperature of water is increased, the new balancing
View SolutionThe resultant resistance value of n resistance each of r ohms and connected is series is X. When those n , resistance are connected in parallel , the resultant values is .
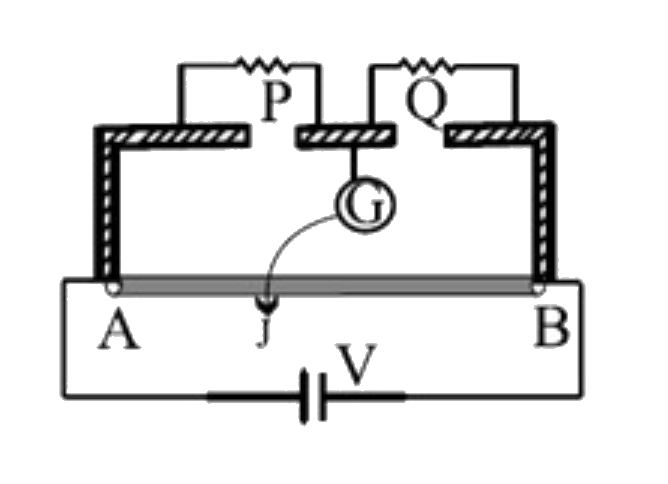
View SolutionIn a meter bridge circuit as shown in the figure, the bridge is balanced when AJ=20 cm. On interchanging P and Q the balance length shifts by
View Solution
