In a meter bridge, the left and right gaps are closed by resistances 2 ohm and 3 ohm respectively. The value of shunt to be connected to 3 ohm resistor to shift the balancing point by 22.5 cm is
3 ohm
1.7 ohm
1 ohm
2 ohm
The correct Answer is:D
To solve the problem step by step, we will follow the principles of the meter bridge and the relationships between resistances and lengths.
1. Understanding the Meter Bridge Setup:
- In a meter bridge, the left gap has a resistance R1=2Ω and the right gap has a resistance R2=3Ω.
- The balancing point is initially at L1 cm from the left end.
2. Finding the Initial Balancing Point:
- The formula for the meter bridge is given by:
R1R2=L1100−L1
- Substituting the values:
23=L1100−L1
- Cross-multiplying gives:
2(100−L1)=3L1
- Expanding and rearranging:
200−2L1=3L1⟹200=5L1⟹L1=2005=40cm
3. Introducing the Shunt Resistance:
- A shunt resistance S is connected in parallel with the 3 ohm resistor.
- The equivalent resistance Req of the 3 ohm resistor and the shunt is given by:
Req=3SS+3
4. Finding the New Balancing Point:
- The new balancing point L2 after shifting is:
L2=L1+22.5=40+22.5=62.5cm
- The new length on the right side is:
100−L2=100−62.5=37.5cm
5. Setting Up the New Balance Equation:
- The new balance condition is:
R1Req=L2100−L2
- Substituting the values:
23SS+3=62.537.5
- Simplifying the right side:
62.537.5=53
- Thus, we have:
2(S+3)3S=53
6. Cross-Multiplying to Solve for S:
- Cross-multiplying gives:
2(S+3)=5S
- Expanding:
2S+6=5S
- Rearranging:
6=5S−2S⟹3S=6⟹S=63=2Ω
7. Conclusion:
- The value of the shunt resistance S that needs to be connected to the 3 ohm resistor to shift the balancing point by 22.5 cm is 2Ω.
Final Answer:
The value of the shunt resistance is 2Ω.
- In a meter bridge, the left gap has a resistance R1=2Ω and the right gap has a resistance R2=3Ω.
- The balancing point is initially at L1 cm from the left end.
- The formula for the meter bridge is given by:
R1R2=L1100−L1
- Substituting the values:
23=L1100−L1
- Cross-multiplying gives:
2(100−L1)=3L1
- Expanding and rearranging:
200−2L1=3L1⟹200=5L1⟹L1=2005=40cm
- A shunt resistance S is connected in parallel with the 3 ohm resistor.
- The equivalent resistance Req of the 3 ohm resistor and the shunt is given by:
Req=3SS+3
- The new balancing point L2 after shifting is:
L2=L1+22.5=40+22.5=62.5cm
- The new length on the right side is:
100−L2=100−62.5=37.5cm
- The new balance condition is:
R1Req=L2100−L2
- Substituting the values:
23SS+3=62.537.5
- Simplifying the right side:
62.537.5=53
- Thus, we have:
2(S+3)3S=53
- Cross-multiplying gives:
2(S+3)=5S
- Expanding:
2S+6=5S
- Rearranging:
6=5S−2S⟹3S=6⟹S=63=2Ω
- The value of the shunt resistance S that needs to be connected to the 3 ohm resistor to shift the balancing point by 22.5 cm is 2Ω.
The value of the shunt resistance is 2Ω.
Topper's Solved these Questions
- APPENDICES ( REVISION EXERCISE )Book:AAKASH SERIESChapter:APPENDICES ( REVISION EXERCISE )Exercise:REVISION EXERCISE (MOVING CHANGES & MEGNETISM)
Explore 95 Videos
- APPENDICES ( REVISION EXERCISE )Book:AAKASH SERIESChapter:APPENDICES ( REVISION EXERCISE )Exercise:REVISION EXERCISE (MAGNETISM AND MATTER )
Explore 52 Videos
- APPENDICES ( REVISION EXERCISE )Book:AAKASH SERIESChapter:APPENDICES ( REVISION EXERCISE )Exercise:REVISION EXERCISE (ELECTRIC POTENTIAL & CAPACITANCE )
Explore 143 Videos
- ALTERNATING CURRENTBook:AAKASH SERIESChapter:ALTERNATING CURRENTExercise:EXERCISE - III
Explore 24 Videos
- APPENDICES (REVISION EXERCISE)Book:AAKASH SERIESChapter:APPENDICES (REVISION EXERCISE)Exercise:LAW OF MOTION
Explore 128 Videos
Similar Questions
In a metre bridge, the gaps are closed by two resistance P and Q and the balance point is obtained at 40cm. When Q is shunted by a resistance of 10Ω, the balance point shifts to 50cm. The values of P and Q are.
 .
.
View SolutionResistance in the two gaps of a meter bridge are 10ohm and 30ohm respectively. If the resistances are interchanged he balance point shifts by
View Solution
Knowledge Check
When a metal conductor connected to left gap of a meter bridge is heated, the balancing point
Ashifts towards rightBshifts towards leftCremains unchangedDremains at zeroIn a meter bridge experiment the ratio of left gap resistance to right gap resistance is 2:3 the balance point from is
A60cmB50cmC40cmD20cm
Two unkonwn resistances X and Y are connected to left and right gaps of a meter bridge and the balancing point is obtained at 80cm from left. When a 10Ω resistance is connected parallel to X, the balancing point is 50cm from left. The values of X and Y respectively are
View SolutionAn unknown resistance R1 is connected is series with a resistance of 10Ω. This combination is connected to one gap of a meter bridge, while other gap is connected to another resistance R2. The balance point is at 50cm Now , when the 10Ω resistance is removed, the balanced point shifts to 40cm Then the value of R1 is.
View SolutionAn unknown resistance R1 is connected is series with a resistance of 10Ω. This combination is connected to one gap of a meter bridge, while other gap is connected to another resistance R2. The balance point is at 50cm Now , when the 10Ω resistance is removed, the balanced point shifts to 40cm Then the value of R1 is.
View SolutionA resistance of 2Ω is connected across one gap of a meter bridge (the length of the wire is 100cm and an unknown resistance, greater than 2Ω, is connected across the other gap. When these resistance are interchanged, the balance point shifts by 20cm. Neglecting any corrections, the unknown resistance is.
(a)3Ω
(b) 4Ω
( c) 5Ω
(d) 6Ω.
View SolutionIn the circuit shown, a meter bridge is in its balanced state. The meter bridge wire has a resistance .1ohm/cm. The value of unknown resistance X and the current drawn from the battery of negligible resistance is
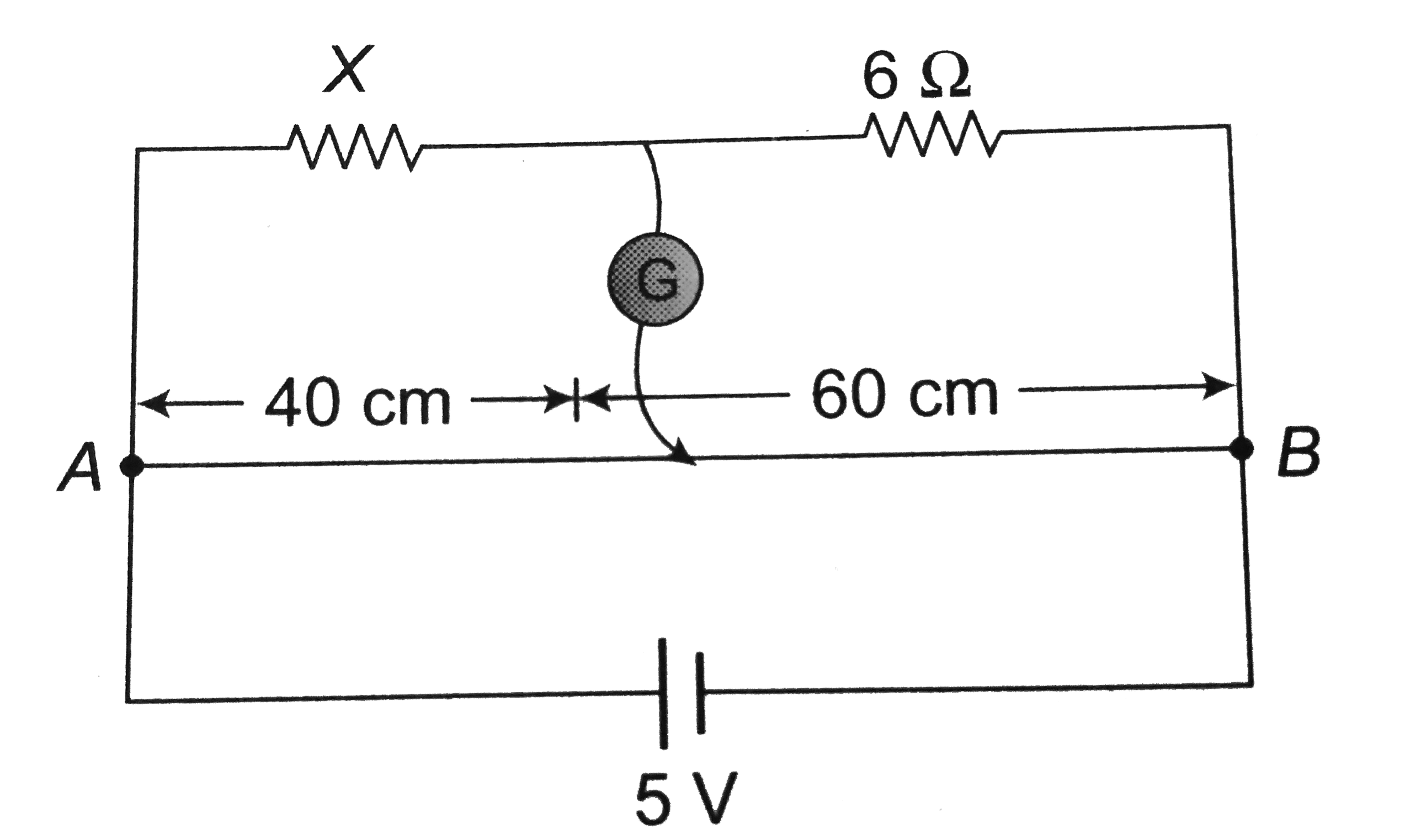
View SolutionIn the circuit shown, a meter bridge is in its balanced state. The meter bridge wire has a resistance .1ohm/cm. The value of unknown resistance X and the current drawn from the battery of negligible resistance is

View Solution