When a conducting wire is connected in the left gap and known resistance in the right gap, the balance length is 75cm. If the wire is cut into 3 equal parts and one part isconnected in the left gap, the balance length
shifts left by 25cms
shifts right by 25cms
shifts left by 50cms
shifts right by 50cms
The correct Answer is:A
To solve the problem step by step, we will analyze the situation using the principles of a meter bridge and the relationship between resistance and balance length.
Step 1: Understanding the Initial Setup
When a conducting wire is connected in the left gap and a known resistance (let's call it R) is in the right gap, the balance length (L) is given as 75 cm.
Hint: Remember that in a meter bridge, the balance condition states that the ratio of the resistances is equal to the ratio of the lengths.
Step 2: Setting Up the Equation for Initial Balance
Using the balance condition:
Ry=75100−75=7525=3
From this, we can deduce:
R=3y
Hint: The lengths on the meter bridge correspond to the resistances in the circuit.
Step 3: Cutting the Wire into Equal Parts
The wire is cut into three equal parts. Therefore, the length of one part (let's call it L') is:
L′=L3=100 cm3≈33.33 cm
The resistance of one part of the wire (let's call it R') can be expressed as:
R′=R3=3y3=y
Hint: Cutting the wire into equal parts divides its resistance by the same factor.
Step 4: Setting Up the Equation for New Balance
Now, we connect one part of the wire (R') in the left gap and the known resistance (R = 3y) remains in the right gap. The new balance length (let's call it L'') can be found using the balance condition again:
R′R=L′′100−L′′
Substituting the values we have:
y3y=L′′100−L′′
This simplifies to:
13=L′′100−L′′
Hint: Use cross-multiplication to solve the equation.
Step 5: Solving for the New Balance Length
Cross-multiplying gives us:
L′′=13(100−L′′)
Multiplying through by 3 to eliminate the fraction:
3L′′=100−L′′
Combining like terms:
4L′′=100
Thus, we find:
L′′=25 cm
Hint: Make sure to isolate L'' to find its value.
Step 6: Conclusion
The balance length when one part of the wire is connected in the left gap is 25 cm.
Final Answer: The new balance length is 25 cm.
When a conducting wire is connected in the left gap and a known resistance (let's call it R) is in the right gap, the balance length (L) is given as 75 cm.
Using the balance condition:
Ry=75100−75=7525=3
From this, we can deduce:
R=3y
The wire is cut into three equal parts. Therefore, the length of one part (let's call it L') is:
L′=L3=100 cm3≈33.33 cm
The resistance of one part of the wire (let's call it R') can be expressed as:
R′=R3=3y3=y
Now, we connect one part of the wire (R') in the left gap and the known resistance (R = 3y) remains in the right gap. The new balance length (let's call it L'') can be found using the balance condition again:
R′R=L′′100−L′′
Substituting the values we have:
y3y=L′′100−L′′
This simplifies to:
13=L′′100−L′′
Cross-multiplying gives us:
L′′=13(100−L′′)
Multiplying through by 3 to eliminate the fraction:
3L′′=100−L′′
Combining like terms:
4L′′=100
Thus, we find:
L′′=25 cm
The balance length when one part of the wire is connected in the left gap is 25 cm.
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:AAKASH SERIESChapter:CURRENT ELECTRICITYExercise:PRACTICE SHEET (EXERCISE - IV LEVEL-II (ADVANCED) (More than One correct answer Type Questions))
Explore 2 Videos
- CURRENT ELECTRICITYBook:AAKASH SERIESChapter:CURRENT ELECTRICITYExercise:PRACTICE SHEET (EXERCISE - IV LEVEL-II (ADVANCED) (Linked Comprehension Type Questions))
Explore 3 Videos
- CURRENT ELECTRICITYBook:AAKASH SERIESChapter:CURRENT ELECTRICITYExercise:PRACTICE SHEET (EXERCISE - III LEVEL-II (ADVANCED) (Integer Type Questions))
Explore 2 Videos
- CURRENT ELECTRICITYBook:AAKASH SERIESChapter:CURRENT ELECTRICITYExercise:PROBLEMS (LEVEL-II)
Explore 27 Videos
- DUAL NATURE OF RADIATION AND MATTERBook:AAKASH SERIESChapter:DUAL NATURE OF RADIATION AND MATTERExercise:PRACTICE EXERCISEX
Explore 42 Videos
Similar Questions
In a metre bridge when the resistance in the left gap is 2Ω and an unknown resistance in the right gap, the balance point is obtained at 40 cm from the zero end. On shunting the unknown resistance with 2Ω find the shift of the balance point on the bridge wire.
View SolutionIn an experiment to determine an unknown resistance, a 100 cm long resistance wire is used. The unknown resistance is kept in the left gap and a known resistance is put into the right gap. The scale to measure length has a least count 1 mm. The null point B is obtained at 40.0 cm from the left gap. We shell determine the percentage error in the computation of unknown resistance.
View Solution
Knowledge Check
When a metal conductor connected to left gap of a meter bridge is heated, the balancing point
Ashifts towards rightBshifts towards leftCremains unchangedDremains at zeroIn a meter bridge experiment the ratio of left gap resistance to right gap resistance is 2:3 the balance point from is
A60cmB50cmC40cmD20cmA wire connected in the left gap of a meter bridge balance a 10Ω resistance in the right gap to a point, which divides the bridge wire in the ratio 3:2. If the length of the wire is 1m. The length of one ohm wire is
A0.057mB0.067mC0.37mD0.134m
In meter bridge when P is kept in left gap, Q is kept in right gap, the balancing length is 40cm. If Q is shunted by 10Ω, the balance point shifts by 10cm. Resistance Q is
View SolutionIf the resistance of potentiometer wire is 15r then calculate the balance length l
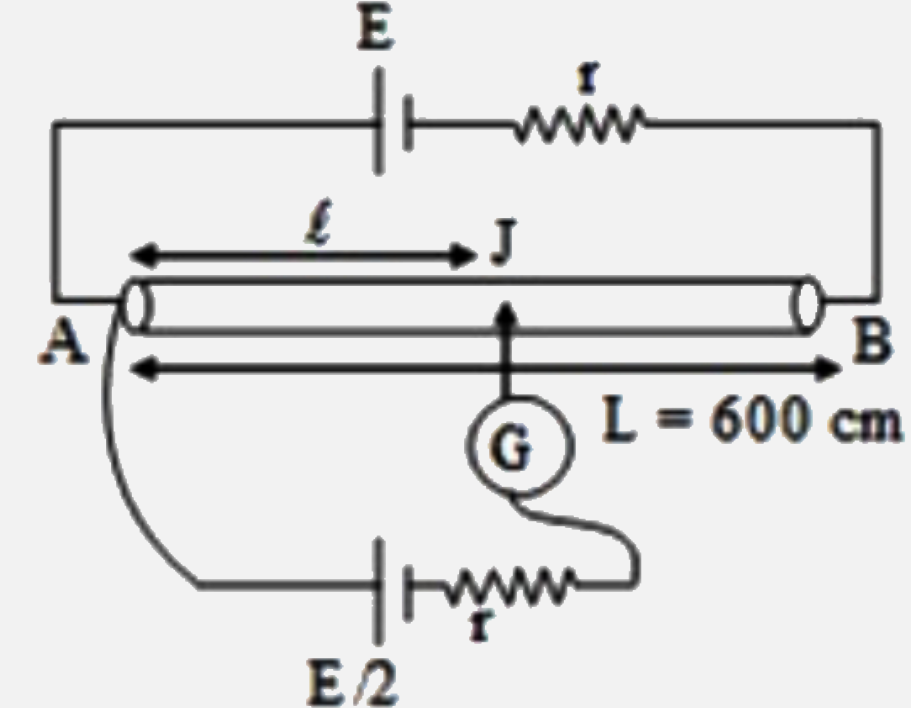
View SolutionIn metre bridge experiment, with a standard resistance in the right gap and a resistance coil dipped in water (in a beaker) in the left gap, the balancing length obtained is '1'. If the temperature of water is increased, the new balancing
View SolutionPower generated across a uniform wire connected across a supply is H. If the wire is cut into n equal parts and all the parts are connected in parallel across the same supply, the total power generated in the wire is
View SolutionA student performs meter bridge experiment to determine specific resistance of a conducting wire of length 10cm and diameter 1mm. When a standard 6Ω resistance is connected on left gap and the given conducting wire is connected on the right gap, the balance points obtained for 60cm length of the meter bridge wire. The specific resistance in Ω−m for material of the given wire is:
View Solution