In an experiment to determine an unknown resistance, a 100 cm long resistance wire is used. The unknown resistance is kept in the left gap and a known resistance is put into the right gap. The scale to measure length has a least count 1 mm. The null point B is obtained at 40.0 cm from the left gap. We shell determine the percentage error in the computation of unknown resistance.
To determine the percentage error in the computation of the unknown resistance using the given information, we can follow these steps:
Step 1: Understand the Setup
We have a 100 cm long resistance wire. The unknown resistance (let's call it x) is placed in the left gap, and a known resistance (let's call it y) is placed in the right gap. The null point is found at 40.0 cm from the left gap.
Step 2: Define the Lengths
Let:
- L1=40.0 cm (the length from the left gap to the null point)
- L2=100−L1=100−40=60.0 cm (the length from the null point to the right gap)
Step 3: Write the Relationship Between Resistances
Using the principle of a Wheatstone bridge, we can express the relationship between the resistances:
xL1=yL2
From this, we can derive:
x=L1L2⋅y
Step 4: Calculate the Error in Measurement
The least count of the scale is 1 mm, which means the maximum error in measurement is ΔL=0.1 cm (since 1 mm = 0.1 cm).
Step 5: Calculate the Percentage Error
The percentage error in x can be calculated using the formula:
Percentage Error in x=ΔL1L1⋅100+ΔL2L2⋅100
Where:
- ΔL1=0.1 cm (error in measuring L1)
- L1=40.0 cm
- ΔL2=0.1 cm (error in measuring L2)
- L2=60.0 cm
Step 6: Substitute Values
Now substituting the values:
1. For L1:
Percentage Error in L1=0.140⋅100=0.25%
2. For L2:
Percentage Error in L2=0.160⋅100≈0.1667%
Step 7: Total Percentage Error
Now, adding the two percentage errors:
Total Percentage Error in x=0.25%+0.1667%≈0.4167%
Step 8: Final Result
Thus, the percentage error in the computation of the unknown resistance x is approximately:
Percentage Error≈0.42%
---
We have a 100 cm long resistance wire. The unknown resistance (let's call it x) is placed in the left gap, and a known resistance (let's call it y) is placed in the right gap. The null point is found at 40.0 cm from the left gap.
Let:
- L1=40.0 cm (the length from the left gap to the null point)
- L2=100−L1=100−40=60.0 cm (the length from the null point to the right gap)
Using the principle of a Wheatstone bridge, we can express the relationship between the resistances:
xL1=yL2
From this, we can derive:
x=L1L2⋅y
The least count of the scale is 1 mm, which means the maximum error in measurement is ΔL=0.1 cm (since 1 mm = 0.1 cm).
The percentage error in x can be calculated using the formula:
Percentage Error in x=ΔL1L1⋅100+ΔL2L2⋅100
- ΔL1=0.1 cm (error in measuring L1)
- L1=40.0 cm
- ΔL2=0.1 cm (error in measuring L2)
- L2=60.0 cm
Now substituting the values:
1. For L1:
Percentage Error in L1=0.140⋅100=0.25%
2. For L2:
Percentage Error in L2=0.160⋅100≈0.1667%
Now, adding the two percentage errors:
Total Percentage Error in x=0.25%+0.1667%≈0.4167%
Thus, the percentage error in the computation of the unknown resistance x is approximately:
Percentage Error≈0.42%
Topper's Solved these Questions
- WAVES AND OSCILLATIONSBook:ALLENChapter:WAVES AND OSCILLATIONSExercise:Part-3(Example)
Explore 32 Videos
- WAVES AND OSCILLATIONSBook:ALLENChapter:WAVES AND OSCILLATIONSExercise:Part-1(Exercise-01)
Explore 53 Videos
- WAVES AND OSCILLATIONSBook:ALLENChapter:WAVES AND OSCILLATIONSExercise:Part-1(Exercise-05)[B]
Explore 42 Videos
- SEMICONDUCTORSBook:ALLENChapter:SEMICONDUCTORSExercise:Part-3(Exercise-4)
Explore 51 Videos
Similar Questions
When a conducting wire is connected in the left gap and known resistance in the right gap, the balance length is 75cm. If the wire is cut into 3 equal parts and one part isconnected in the left gap, the balance length
View SolutionFor the post office arrangement to determine the value of unknown resistance, the unknown resistance should be connected between.
View Solution
Knowledge Check
In a meter bridge experiment the ratio of left gap resistance to right gap resistance is 2:3 the balance point from is
A60cmB50cmC40cmD20cm
In a metre bridge when the resistance in the left gap is 2Ω and an unknown resistance in the right gap, the balance point is obtained at 40 cm from the zero end. On shunting the unknown resistance with 2Ω find the shift of the balance point on the bridge wire.
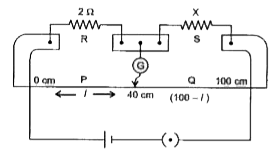
View SolutionIn a meter bridge circuit, resistance, in the left hand gap is 2Ω and an unknown resistance X is in the right hand gap as shown in figure below. The null point is found to be 40 cm from the left end of the wire. What resistance should be connected to X so that the new null point is 50 cm from the left end of the wire ?
View SolutionAn unknown resistance r si determined in terms of a standared resistance R=100Ω by using potentiometer. The potential difference across r is balanced againt 45cm length of the wire and that (r+R) is obtained at 70cm of the wire. Find the value of the unknown resistance.
View SolutionIn a meter-bridge experiment with a resistance R1 in left gap and a resistance X in a right gap. null point is obtained at 40cm from the left emf. With a resistance R2 in the left gap, the null point is obtainned at 50cm from left hand. Find the position of the left gap is containing R1 and R2 (i) in series and (ii) in parallel.
View SolutionIn a metre bridge experiment to determine unknown resistance of a coil, how is position of the null point affected if:
(i) Galvanometer and cell are interchanged?
(ii) Known and unknown resistances are interchanged?
View SolutionIn a meter bridge experment, the value of unknown resistance is 2Ω. To get tehbalancing point at 40 cm distance form the same end, the resistance in the resistance box will be :
View SolutionIn a potentiometer experiment, the balancing length with a resistance of 2Ω is found to be 100cm, while that of an unknown resistance is 500cm. Calculate the value of the unknown resistance.
View Solution