In the circuit shown, voltmeter is ideal and its least count is 0.1 V. The least count of ammeter is 1 mA. Reading of the voltmeter be 30.0 V and the reading of ammeter is 0.020 A. We shell calculate the value of resistance R within error limits.
To solve the problem of calculating the resistance R within error limits, we can follow these steps:
Step 1: Identify Given Values
- Voltage V=30.0V
- Current I=0.020A
- Least count of voltmeter δV=0.1V
- Least count of ammeter δI=1mA=0.001A
Step 2: Calculate Resistance Using Ohm's Law
According to Ohm's Law, the resistance R can be calculated using the formula:
R=VI
Substituting the given values:
R=30.0V0.020A=1500Ω=1.50kΩ
Step 3: Calculate the Error in Resistance
To find the error in resistance, we use the formula for relative error:
ΔRR=ΔVV+ΔII
Where:
- ΔR is the absolute error in resistance.
- ΔV is the least count of the voltmeter.
- ΔI is the least count of the ammeter.
Rearranging gives us:
ΔR=R(ΔVV+ΔII)
Step 4: Substitute the Values
Now we substitute the known values into the error formula:
ΔR=1500Ω(0.1V30.0V+0.001A0.020A)
Calculating each term:
1. 0.130.0=0.00333
2. 0.0010.020=0.05
Adding these:
0.130.0+0.0010.020=0.00333+0.05=0.05333
Now substituting back:
ΔR=1500Ω×0.05333≈80Ω=0.080kΩ
Step 5: Write the Final Result
The resistance R with its error can be expressed as:
R=1.50kΩ±0.080kΩ
Final Answer
Thus, the value of resistance R within error limits is:
R=1.50kΩ±0.080kΩ
---
- Voltage V=30.0V
- Current I=0.020A
- Least count of voltmeter δV=0.1V
- Least count of ammeter δI=1mA=0.001A
According to Ohm's Law, the resistance R can be calculated using the formula:
R=VI
Substituting the given values:
R=30.0V0.020A=1500Ω=1.50kΩ
To find the error in resistance, we use the formula for relative error:
ΔRR=ΔVV+ΔII
Where:
- ΔR is the absolute error in resistance.
- ΔV is the least count of the voltmeter.
- ΔI is the least count of the ammeter.
ΔR=R(ΔVV+ΔII)
Now we substitute the known values into the error formula:
ΔR=1500Ω(0.1V30.0V+0.001A0.020A)
1. 0.130.0=0.00333
2. 0.0010.020=0.05
0.130.0+0.0010.020=0.00333+0.05=0.05333
ΔR=1500Ω×0.05333≈80Ω=0.080kΩ
The resistance R with its error can be expressed as:
R=1.50kΩ±0.080kΩ
Thus, the value of resistance R within error limits is:
R=1.50kΩ±0.080kΩ
Topper's Solved these Questions
- WAVES AND OSCILLATIONSBOOK - ALLENCHAPTER - WAVES AND OSCILLATIONSEXERCISE - Part-3(Example)
32 Videos
- WAVES AND OSCILLATIONSBOOK - ALLENCHAPTER - WAVES AND OSCILLATIONSEXERCISE - Part-1(Exercise-01)
53 Videos
- WAVES AND OSCILLATIONSBOOK - ALLENCHAPTER - WAVES AND OSCILLATIONSEXERCISE - Part-1(Exercise-05)[B]
42 Videos
- SEMICONDUCTORSBOOK - ALLENCHAPTER - SEMICONDUCTORSEXERCISE - Part-3(Exercise-4)
51 Videos
Similar Questions
An ideal voltmeter V and ideal ammeter A are connected in a circuit as shown in the figure. If the reading of the voltmeter is 32 V, the reading of ammeter will be
View SolutionIn the circuit figure, the voltmeter reads 30 V. The resistance of the voltmeter is
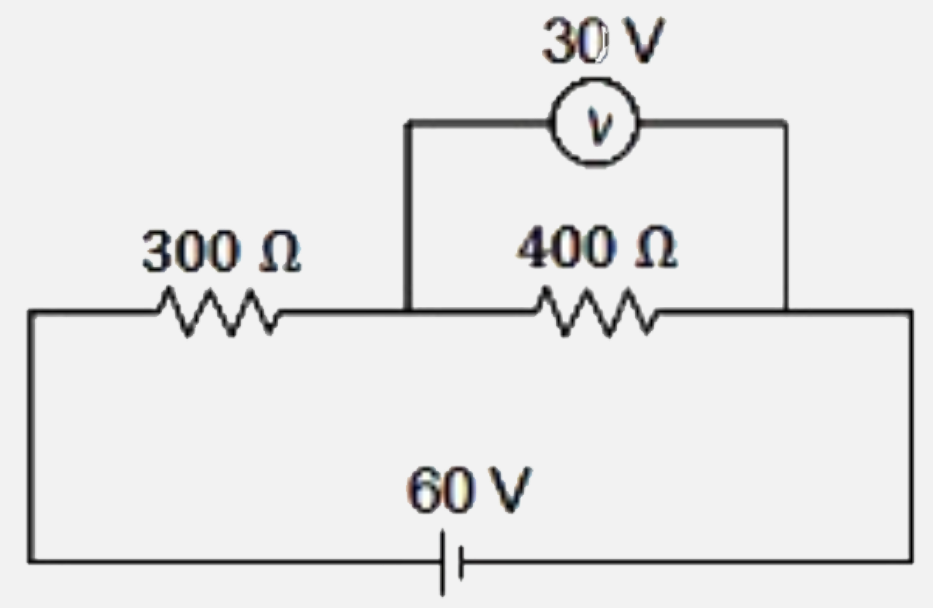
View SolutionIn the circuit shown in figure ammeter and voltmeter are ideal. If E=4V,R=9Ω and r=1Ω then readings of ammeter and voltmeter are
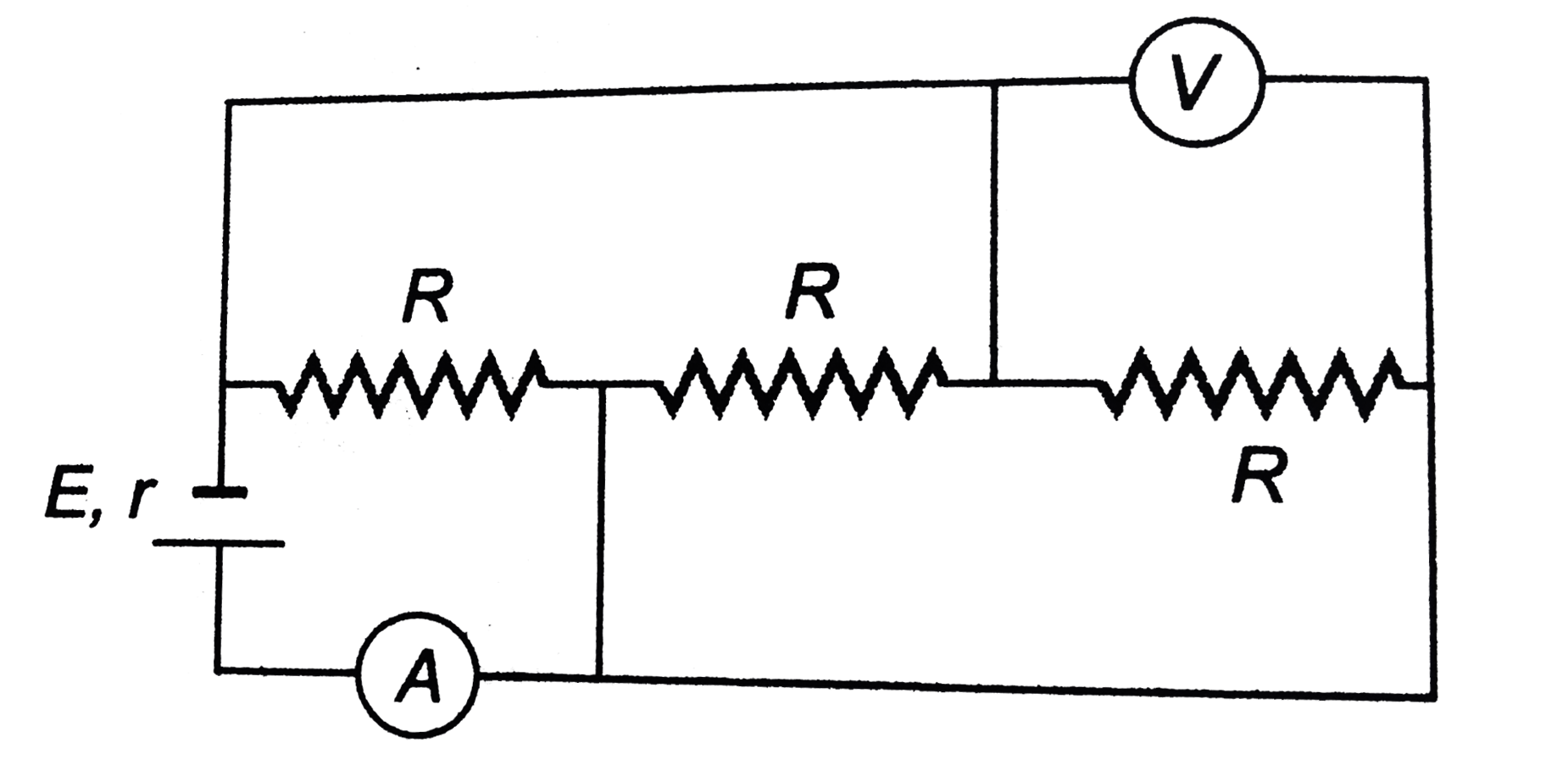
View SolutionIn the circuit shown in figure ammeter and voltmeter are ideal. If E=4V,R=9Ω and r=1Ω then readings of ammeter and voltmeter are

View SolutionIn the circuit shown below, each battery is 5V and has an internal resistance of 0.2 ohm.
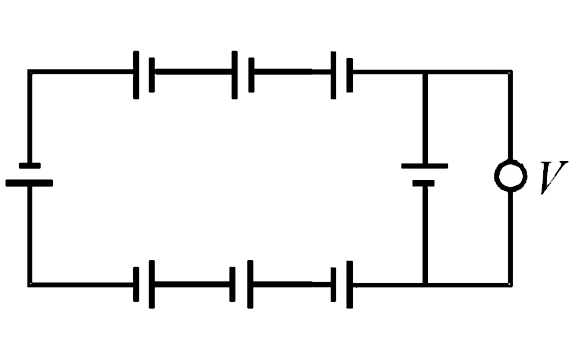
The reading in the ideal voltmeter V is .
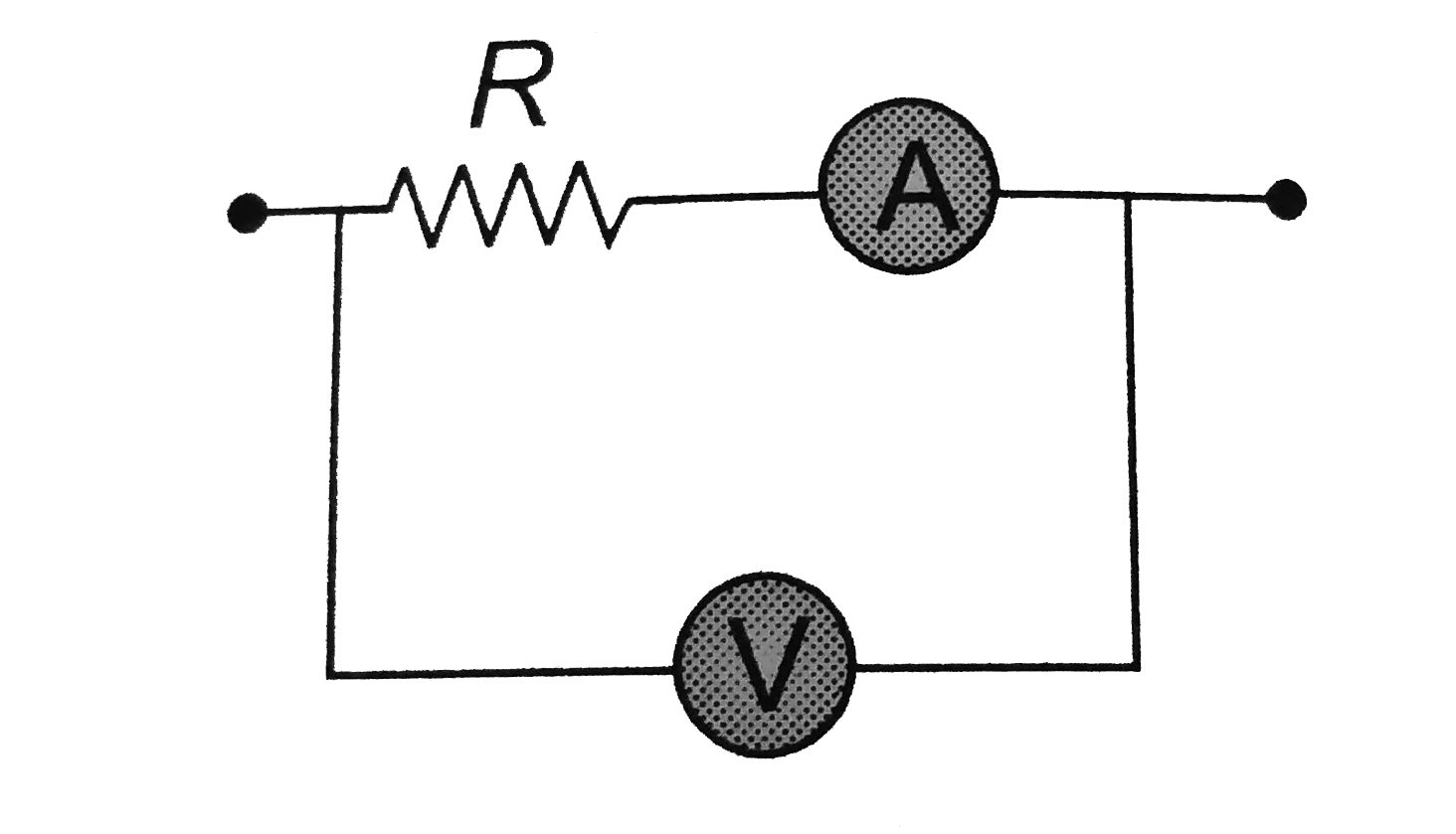
View SolutionIn the circuit shown the resistance of voltmeter is 10000ohm and that of ammeter is 20ohm. The ammeter reading is 0.10amp and voltmeter reading is 12 volts. Then R is equal to
View SolutionIn the circuit shown, A and V are ideal ammeter and voltmeter respectively. Reading of the voltmeter will be

View Solutionin the circuit shown in the figure, each battery is of 5 V and has an internal resistance of 0.2 Omega What is the reading of the ideal voltmeter V
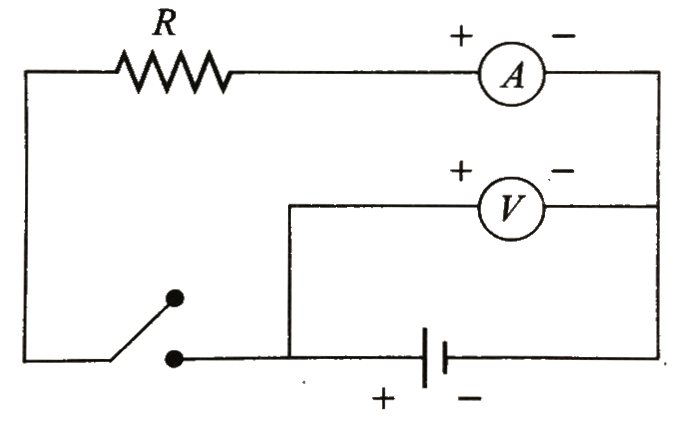
View SolutionIn the circuit shown in Fig. 6.50, an idel ammeter and an ideal voltmeter are used. Whan the key is open, the voltmeter reads 1.53V. When the key is closed, the ammeter reads 1.0A and the voltmeter reads 1.03V. The resistance R is
View SolutionThe power dissipated in resistor R3 shown in the figure is 15 W. The reading the ammeter is 500 mA and the reading of the voltmeter is 10 V. Ammeter, voltmeter and battery are ideal.

Find the resistance R1
View Solution
