When un known resistance and a resistance of 4Ω are used in the left and right gaps of a meter bridge, the balance point is 50cm. the shift in the balance point if a 4Ω resistance is now connected parallel to the resistor in right gap ______
1003cm
503cm
3003cm
4005cm
The correct Answer is:B
To solve the problem step by step, we will analyze the situation using the principles of a meter bridge and the concept of resistances in parallel.
Step 1: Understand the initial setup
We have a meter bridge with an unknown resistance x on the left side and a known resistance of 4Ω on the right side. The balance point is at 50cm.
Step 2: Use the meter bridge formula
The meter bridge operates on the principle that the ratio of the resistances is equal to the ratio of the lengths from the ends of the bridge to the balance point. The formula is given by:
xy=l1l2
Where:
- x = unknown resistance
- y = known resistance (4 Ω)
- l1 = length from one end to the balance point (50 cm)
- l2 = length from the other end to the balance point (100 cm - 50 cm = 50 cm)
Step 3: Substitute known values
Substituting the known values into the equation:
x4=5050
This simplifies to:
x4=1
Step 4: Solve for the unknown resistance
From the equation, we find:
x=4Ω
Step 5: Introduce the new scenario
Now, we connect a 4Ω resistor in parallel with the 4Ω resistor already present in the right gap. The equivalent resistance y′ of two 4Ω resistors in parallel can be calculated using the formula:
1y′=14+14
Step 6: Calculate the equivalent resistance
Calculating the equivalent resistance:
1y′=14+14=24=12
Thus,
y′=2Ω
Step 7: Set up the new balance point equation
Now, we set up the equation for the new balance point using the new equivalent resistance y′:
xy′=l′1100−l′1
Substituting the known values:
42=l′1100−l′1
Step 8: Solve for the new balance point l′1
Cross-multiplying gives:
4(100−l′1)=2l′1
Expanding and rearranging:
400−4l′1=2l′1
400=6l′1
l′1=4006=2003cm
Step 9: Calculate the shift in the balance point
The initial balance point was at 50cm. The new balance point is 2003cm. The shift in the balance point Δl is:
Δl=l′1−l1=2003−50
Step 10: Solve for the shift
Converting 50 to a fraction with a common denominator:
50=1503
Now, substituting:
Δl=2003−1503=503cm
Final Answer
The shift in the balance point is 503cm.
---
We have a meter bridge with an unknown resistance x on the left side and a known resistance of 4Ω on the right side. The balance point is at 50cm.
The meter bridge operates on the principle that the ratio of the resistances is equal to the ratio of the lengths from the ends of the bridge to the balance point. The formula is given by:
- x = unknown resistance
- y = known resistance (4 Ω)
- l1 = length from one end to the balance point (50 cm)
- l2 = length from the other end to the balance point (100 cm - 50 cm = 50 cm)
Substituting the known values into the equation:
From the equation, we find:
Now, we connect a 4Ω resistor in parallel with the 4Ω resistor already present in the right gap. The equivalent resistance y′ of two 4Ω resistors in parallel can be calculated using the formula:
Calculating the equivalent resistance:
Now, we set up the equation for the new balance point using the new equivalent resistance y′:
Cross-multiplying gives:
400=6l′1
l′1=4006=2003cm
The initial balance point was at 50cm. The new balance point is 2003cm. The shift in the balance point Δl is:
Converting 50 to a fraction with a common denominator:
The shift in the balance point is 503cm.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - PRACTICE SHEET (EXERCISE - IV LEVEL-II (ADVANCED) (More than One correct answer Type Questions))
2 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - PRACTICE SHEET (EXERCISE - IV LEVEL-II (ADVANCED) (Linked Comprehension Type Questions))
3 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - PRACTICE SHEET (EXERCISE - III LEVEL-II (ADVANCED) (Integer Type Questions))
2 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - PROBLEMS (LEVEL-II)
27 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - AAKASH SERIESCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - PRACTICE EXERCISEX
42 Videos
Similar Questions
Two unkonwn resistances X and Y are connected to left and right gaps of a meter bridge and the balancing point is obtained at 80cm from left. When a 10Ω resistance is connected parallel to X, the balancing point is 50cm from left. The values of X and Y respectively are
View SolutionTwo unknown resistances X and Y are placed on the left and right gaps of a meter bridge. The null point in the galvanometer is obtained at a distance of 80cm from left. A resistance of 100Ω is now connected in parallel across X. The null point is then found by shifting the sliding contact toward left by 20cm. Calculate X and Y.
View Solution
Knowledge Check
When a metal conductor connected to left gap of a meter bridge is heated, the balancing point
Ashifts towards rightBshifts towards leftCremains unchangedDremains at zero
The resistance in the left and right gaps of a balanced meter bridge are R1 and R1. The balanced point is 50cm. If a resistance of 24Ω is connected in parallel to R2, the balance point is 70cm. The value of R1 or R2 is.
View SolutionA copper strip is introduced in the left gap and a resistance R−0.4Ω is placed in the right gap of a meter bridge experiment. The balance points before and after interchanging the copper strip and the resistance R are 30 cm and 60 cm respectively. The resistance per unit length of the bridge wire is
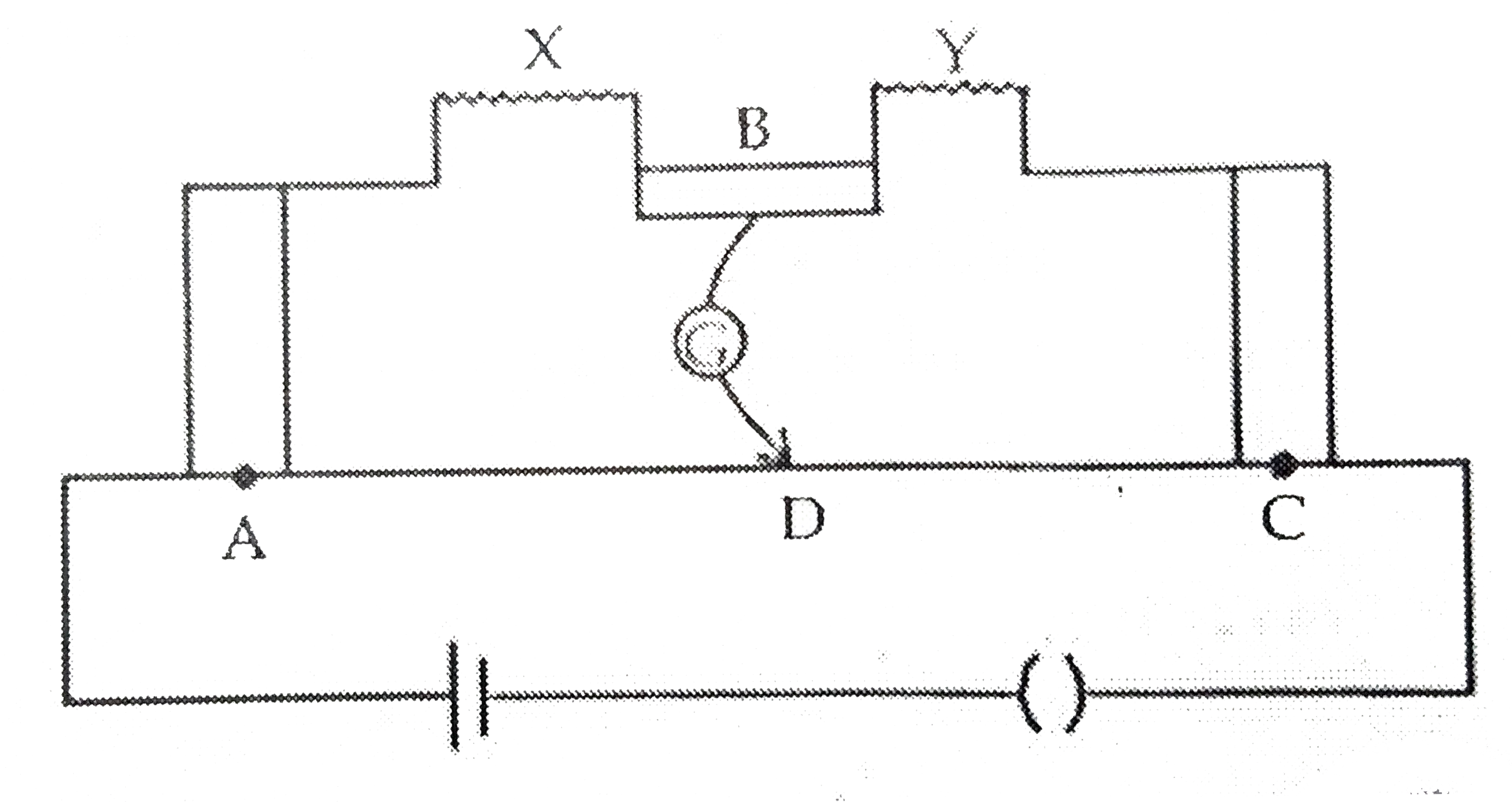
View SolutionThe figure shows experimental set up of a meter bridge. When the two unknown resistances X and Y are inserted, the null point D is obtained 40 cm from the end A. When a resistance of 10Ω is connected in series with X, the null point shifts by 10 cm. Find the position of the null point when the 10Ω resistance is instead connected in series with resistance 'Y'. Determine the value of the resistance X and Y
View SolutionA 6Ω resistance is connected in the left gap of a meter bridge. In the second gap 3Ω and 6Ω are joined in parallel. The balance point of the bridge is at _______
View SolutionIn meter bridge when P is kept in left gap, Q is kept in right gap, the balancing length is 40cm. If Q is shunted by 10Ω, the balance point shifts by 10cm. Resistance Q is
View SolutionTwo unknown resistances are connected in two gaps of a meter-bridge. The null point is obtained at 40 cm from left end. A 30Ω resistance is connected in series with the smaller of the two resistances, the null point shifts by 20 cm to the right end. The value of smaller resistance in Ω is
View SolutionResistance in the two gaps of a meter bridge are 10ohm and 30ohm respectively. If the resistances are interchanged he balance point shifts by
View Solution
