When two identical cells are connected either in series or in parallel across a 4 ohm resistor, they send the same current through it. The internal resistance of the cell in ohm is
1.2
2
4
4.8
The correct Answer is:C
To solve the problem, we need to analyze the two configurations of the cells (series and parallel) and set up equations based on Ohm's Law and the properties of the circuits.
1. Define Variables:
- Let the electromotive force (emf) of each cell be E.
- Let the internal resistance of each cell be r.
- The external resistance (the resistor across which the cells are connected) is given as R=4Ω.
2. Series Connection:
- When the two cells are connected in series, the total emf is 2E and the total internal resistance is 2r.
- The total resistance in the circuit is R+2r.
- Using Ohm's Law, the current Is in the series circuit can be expressed as:
Is=2ER+2r=2E4+2r
3. Parallel Connection:
- When the two cells are connected in parallel, the total emf remains E and the total internal resistance becomes r2.
- The total resistance in this circuit is R+r2.
- The current Ip in the parallel circuit can be expressed as:
Ip=ER+r2=E4+r2
4. Equating Currents:
- According to the problem, the currents through the resistor in both configurations are the same, so we set Is=Ip:
2E4+2r=E4+r2
5. Simplifying the Equation:
- We can cancel E from both sides (assuming E≠0):
24+2r=14+r2
- Cross-multiplying gives:
2(4+r2)=1(4+2r)
- Expanding both sides:
8+r=4+2r
6. Solving for r:
- Rearranging the equation:
8−4=2r−r
4=r
7. Conclusion:
- The internal resistance r of each cell is 4Ω.
Final Answer:
The internal resistance of the cell is 4Ω.
---
- Let the electromotive force (emf) of each cell be E.
- Let the internal resistance of each cell be r.
- The external resistance (the resistor across which the cells are connected) is given as R=4Ω.
- When the two cells are connected in series, the total emf is 2E and the total internal resistance is 2r.
- The total resistance in the circuit is R+2r.
- Using Ohm's Law, the current Is in the series circuit can be expressed as:
Is=2ER+2r=2E4+2r
- When the two cells are connected in parallel, the total emf remains E and the total internal resistance becomes r2.
- The total resistance in this circuit is R+r2.
- The current Ip in the parallel circuit can be expressed as:
Ip=ER+r2=E4+r2
- According to the problem, the currents through the resistor in both configurations are the same, so we set Is=Ip:
2E4+2r=E4+r2
- We can cancel E from both sides (assuming E≠0):
24+2r=14+r2
- Cross-multiplying gives:
2(4+r2)=1(4+2r)
- Expanding both sides:
8+r=4+2r
- Rearranging the equation:
8−4=2r−r
4=r
- The internal resistance r of each cell is 4Ω.
The internal resistance of the cell is 4Ω.
Topper's Solved these Questions
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MOVING CHANGES & MEGNETISM)
95 Videos
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MAGNETISM AND MATTER )
52 Videos
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (ELECTRIC POTENTIAL & CAPACITANCE )
143 Videos
- ALTERNATING CURRENTBOOK - AAKASH SERIESCHAPTER - ALTERNATING CURRENTEXERCISE - EXERCISE - III
24 Videos
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - LAW OF MOTION
128 Videos
Similar Questions
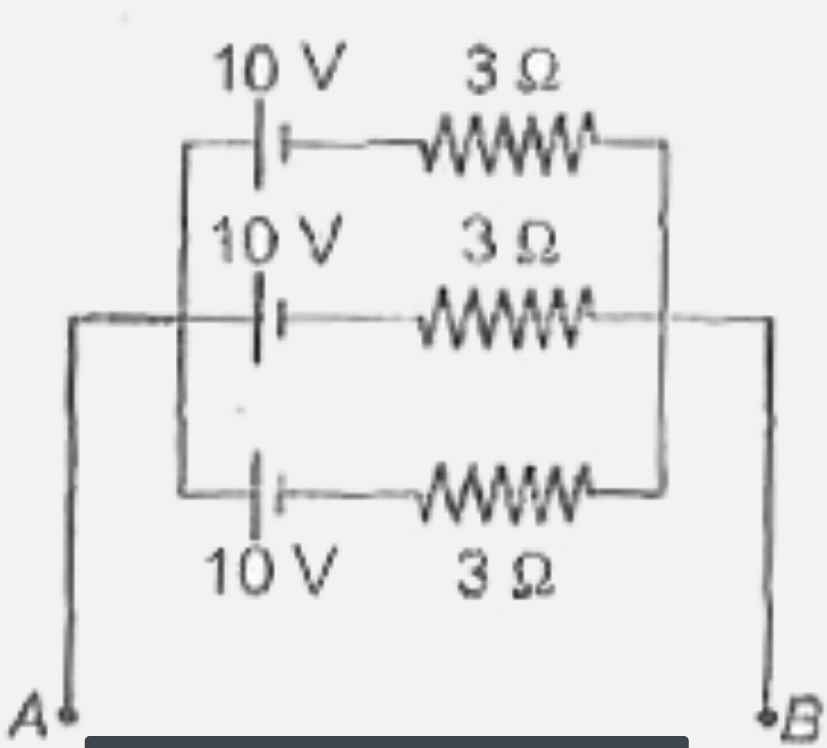
Three identical cells are connected in parallel across AB. Net across AB is
View SolutionN identical cells whether joined together in series or in parallel, give the same current, when connected to an external resistance of 'R'. The internal resistance of each cell is:-
View SolutionBy a cell a current of 0.9 A flows through 2 ohm resistor and 0.3A through 7 ohm resistor. The internal resistance of the cell is
View SolutionIn a mixed grouping of identical cells, five rows are connected in parallel and each row contains 10 cells. This combination sends a current I through an external resistance of 20Ω. if the emf and internal resistance of each cell is 1.5 V and 1Ω, respectively then find the value of I.
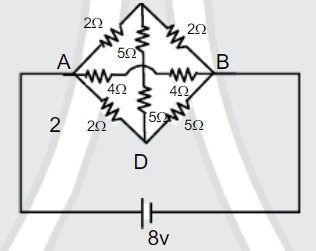
View SolutionFind current through 4ohm resistance
View SolutionA 50V battery is connected across a 10 ohm resistor. The current is 4.5A is flowing through the resistor then the internal resistance of the battery is
View SolutionThe reading on a high resistance voltmeter when a cell is connected across it is 3 V. When the terminals of the cell are also connected to a resistance of 4 Ω, then the voltmeter reading drops to 1.2 V. Find the internal resistance of the cell.
View SolutionA cell develops the same power across two resistances R1 and R2 separately. The internal resistance of the cell is
View SolutionA cell develops the same power across two resistances R1 and R2 separately. The internal resistance of the cell is
View SolutionWrite any two factors on which internal resistance of a cell depends . The reading on a high resistance voltmeter , when a cell is connected across it , is 2.0 V . When the terminals of the cell are also connected to a resistance of 3Ω as shown in the circuit , the voltmeter reading drops to 1.5 V . Find the internal resistance of the cell.
View Solution
