A d.c main supply of e.m.f 220 V is connected across a storage battery of e.m.f 200 V through a resistance of 1Ω. The battery terminals are connected to an external resistance R. The minimum value of R so that a current passes through the battery to charge it is:
Zero
7Ω
9Ω
11Ω
The correct Answer is:D
To solve the problem, we need to find the minimum value of the external resistance R such that a current flows through the battery to charge it. Here’s the step-by-step solution:
Step 1: Understand the Circuit
We have a DC supply of 220 V connected to a storage battery of 200 V through a resistance of 1 Ω. The battery is also connected to an external resistance R.
Step 2: Apply Kirchhoff's Voltage Law
According to Kirchhoff's Voltage Law, the sum of the potential differences in a closed loop must equal zero. The potential across the battery and the external resistance must equal the supply voltage.
Step 3: Write the Equation
The equation based on Kirchhoff's law can be written as:
Vsource=Vbattery+Vresistor
Where:
- Vsource=220V
- Vbattery=200V+I⋅Rinternal
- Vresistor=I⋅R
Step 4: Substitute Values
Substituting the known values into the equation:
220=200+I⋅1+I⋅R
This simplifies to:
220=200+I+I⋅R
20=I+I⋅R
Step 5: Factor Out I
We can factor out I from the right side:
20=I(1+R)
Step 6: Solve for R
To find R, we rearrange the equation:
R=20I−1
Step 7: Find Minimum Current I
For the battery to charge, the current I must be greater than 0. The minimum current occurs when the potential difference across the battery is just enough to allow current to flow.
Step 8: Set I to a Small Value
Assuming I is a small positive value, we can set I=20A (this is a hypothetical maximum current to ensure charging):
R=2020−1=1−1=0Ω
Step 9: Find the Minimum Value of R
To ensure that current flows through the battery, we can set I to a value that allows R to be positive. If we set I=20A:
R=20I−1
To find a practical value for R, we can set I=20A as a threshold:
R=201−1=20−1=19Ω
Conclusion
Thus, the minimum value of R so that a current passes through the battery to charge it is:
Rmin=11Ω
We have a DC supply of 220 V connected to a storage battery of 200 V through a resistance of 1 Ω. The battery is also connected to an external resistance R.
According to Kirchhoff's Voltage Law, the sum of the potential differences in a closed loop must equal zero. The potential across the battery and the external resistance must equal the supply voltage.
The equation based on Kirchhoff's law can be written as:
Vsource=Vbattery+Vresistor
Where:
- Vsource=220V
- Vbattery=200V+I⋅Rinternal
- Vresistor=I⋅R
Substituting the known values into the equation:
220=200+I⋅1+I⋅R
This simplifies to:
220=200+I+I⋅R
20=I+I⋅R
We can factor out I from the right side:
20=I(1+R)
To find R, we rearrange the equation:
R=20I−1
For the battery to charge, the current I must be greater than 0. The minimum current occurs when the potential difference across the battery is just enough to allow current to flow.
Assuming I is a small positive value, we can set I=20A (this is a hypothetical maximum current to ensure charging):
R=2020−1=1−1=0Ω
To ensure that current flows through the battery, we can set I to a value that allows R to be positive. If we set I=20A:
R=20I−1
To find a practical value for R, we can set I=20A as a threshold:
R=201−1=20−1=19Ω
Thus, the minimum value of R so that a current passes through the battery to charge it is:
Rmin=11Ω
Topper's Solved these Questions
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MOVING CHANGES & MEGNETISM)
95 Videos
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MAGNETISM AND MATTER )
52 Videos
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (ELECTRIC POTENTIAL & CAPACITANCE )
143 Videos
- ALTERNATING CURRENTBOOK - AAKASH SERIESCHAPTER - ALTERNATING CURRENTEXERCISE - EXERCISE - III
24 Videos
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - LAW OF MOTION
128 Videos
Similar Questions
An uncharged capacitor of capacitance 100μF is connected to a battery of emf 20V at t = 0 through a resistance 10Ω, then
(ii) time at which the rate has time miximum value is
View SolutionA battery is of emt E and internal resistance R. The value of external resistance r so that the power across eternal resistance is maximum :
View SolutionAn inductor of 3H is connected to a battery of emf 6V through a resistance of 100 Ω. Calculate the time constant. What will be the maximum value of current in the circuit ?
View SolutionA battery of e.m.f. 10V and internal resistance 0.5ohm is connected across a variable resistance R. The value of R for which the power delivered in it is maximum is given by
View SolutionA battery of emf 2 V and initial resistance 1Ω is
connected across terminals A and B of the circuit shown
in figure
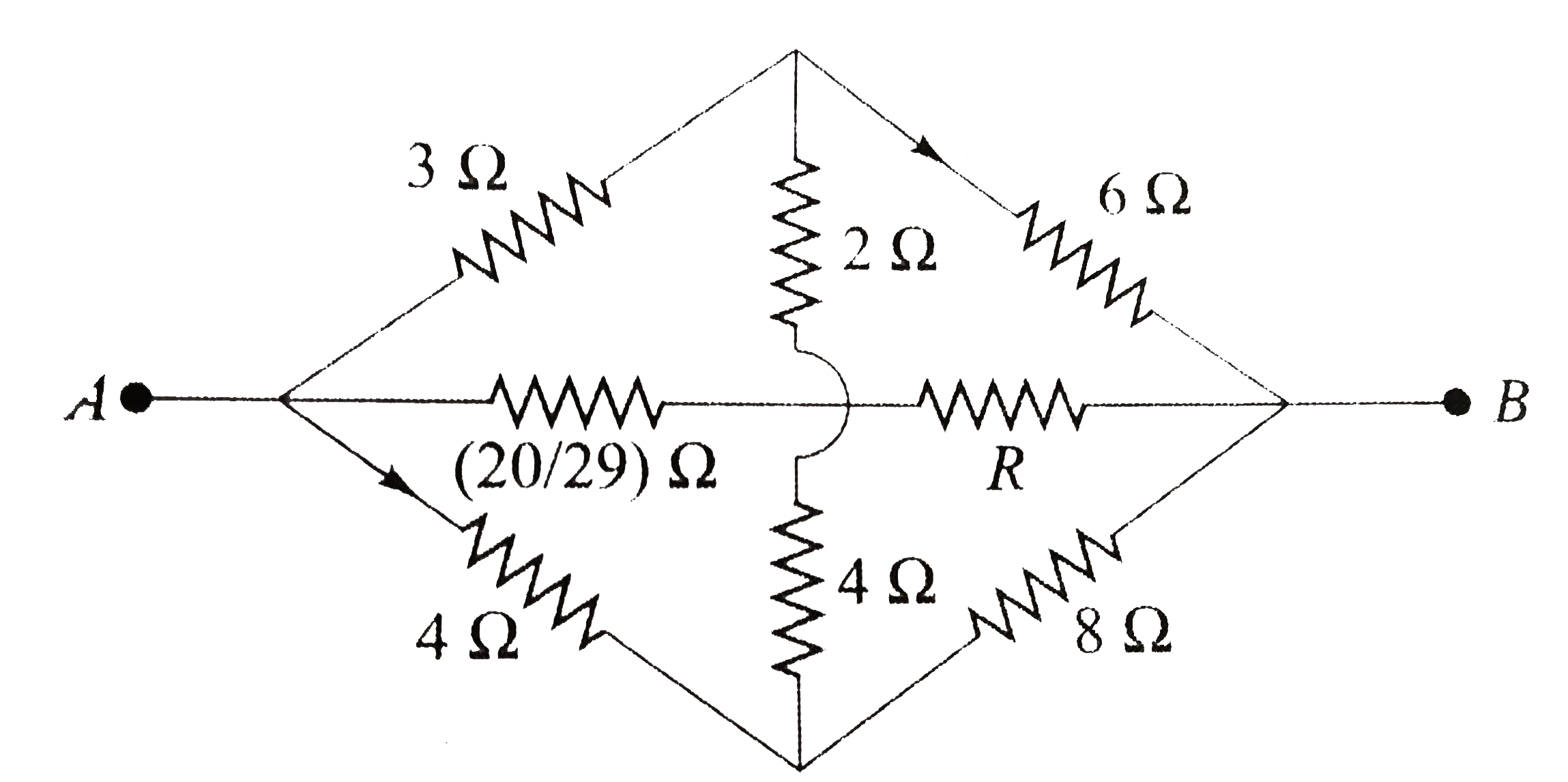 .
.
View SolutionA battery of emf 2V and internal resistance 0.5(Ω)is connected across a resistance 1.5(Ω). Find the current flow through battery ?
View SolutionA battery has e.m.f. 4 V and internal resistance r . When this battery is connected to an external resistance of 2 ohms , a current of 1 amp . flows in the circuit. How much current will flow if the terminals of the battery are connected directly
View SolutionA battery of e.m.f. 15 V and internal resistance 3Ω is connected to two resistors 3 Ω and 6 Ω connected in parallel. Find :
the current through the battery,
View SolutionA battery of 10V is connected to a resistance of 20Ω through a variable resistance R. If the variable resistance R is increased at the rate of 5Ω min−1, then the amount of charge that passes through the battery in 4 min is
View SolutionA P-N junction diode connected to a battery of e.m.f. 4.5 V and an external resistance of 1000Ω. What is the value of current in the circuit, if potential barrier in the diode =0.5V
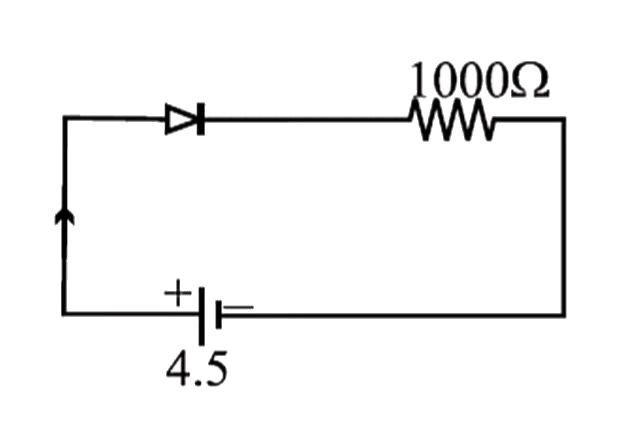
View Solution
