Two identical condensers M and N are connected in series with a battery. The space between the plates of 'M' is completely filled with dielectric medium of dielectric constant 8 and a copper plate of thickness d/ 2 is introduced between the plates of N. (d = distance of separation of the plates). Then the potentials of M and N are respectively.
1:4
4:1
3:8
1:6
The correct Answer is:A
To solve the problem, we need to analyze the two capacitors M and N connected in series and calculate their respective potentials. Here’s a step-by-step solution:
Step 1: Understand the configuration of capacitors
We have two identical capacitors, M and N. Capacitor M is filled with a dielectric medium of dielectric constant k=8. Capacitor N has a copper plate of thickness d2 inserted between its plates, where d is the distance between the plates.
Step 2: Calculate the capacitance of capacitor M
The capacitance of a capacitor filled with a dielectric is given by:
Cm=k⋅C0
where C0 is the original capacitance without the dielectric. Since k=8, we have:
Cm=8C0
Step 3: Calculate the capacitance of capacitor N
For capacitor N, the effective distance between the plates after inserting the copper plate is d−d2=d2. The capacitance of a capacitor is inversely proportional to the distance between the plates:
Cn=ϵ0Ad2=2ϵ0Ad=2C0
Step 4: Relate the charges and potentials in series
Since capacitors M and N are connected in series, the charge Q on both capacitors is the same. The relationship between charge, capacitance, and potential is given by:
Q=CmVm=CnVn
From this, we can express the potentials:
Vm=QCmandVn=QCn
Step 5: Find the ratio of potentials
Using the expressions for Vm and Vn, we can find the ratio:
VmVn=CnCm
Substituting the values of capacitance:
VmVn=2C08C0=28=14
Step 6: Conclusion
Thus, the potentials of M and N are in the ratio:
Vm:Vn=1:4
We have two identical capacitors, M and N. Capacitor M is filled with a dielectric medium of dielectric constant k=8. Capacitor N has a copper plate of thickness d2 inserted between its plates, where d is the distance between the plates.
The capacitance of a capacitor filled with a dielectric is given by:
Cm=k⋅C0
where C0 is the original capacitance without the dielectric. Since k=8, we have:
Cm=8C0
For capacitor N, the effective distance between the plates after inserting the copper plate is d−d2=d2. The capacitance of a capacitor is inversely proportional to the distance between the plates:
Cn=ϵ0Ad2=2ϵ0Ad=2C0
Since capacitors M and N are connected in series, the charge Q on both capacitors is the same. The relationship between charge, capacitance, and potential is given by:
Q=CmVm=CnVn
From this, we can express the potentials:
Vm=QCmandVn=QCn
Using the expressions for Vm and Vn, we can find the ratio:
VmVn=CnCm
Substituting the values of capacitance:
VmVn=2C08C0=28=14
Thus, the potentials of M and N are in the ratio:
Vm:Vn=1:4
Topper's Solved these Questions
- APPENDICES ( REVISION EXERCISE )Book:AAKASH SERIESChapter:APPENDICES ( REVISION EXERCISE )Exercise:REVISION EXERCISE (CUTTENT ELECTRICITY )
Explore 108 Videos
- APPENDICES ( REVISION EXERCISE )Book:AAKASH SERIESChapter:APPENDICES ( REVISION EXERCISE )Exercise:REVISION EXERCISE (MOVING CHANGES & MEGNETISM)
Explore 95 Videos
- APPENDICES ( REVISION EXERCISE )Book:AAKASH SERIESChapter:APPENDICES ( REVISION EXERCISE )Exercise:REVISION EXERCISE (MAGNETISM AND MATTER )
Explore 52 Videos
- ALTERNATING CURRENTBook:AAKASH SERIESChapter:ALTERNATING CURRENTExercise:EXERCISE - III
Explore 24 Videos
- APPENDICES (REVISION EXERCISE)Book:AAKASH SERIESChapter:APPENDICES (REVISION EXERCISE)Exercise:LAW OF MOTION
Explore 128 Videos
Similar Questions
Two parallel plate capacitors, each of capacitance 40 muF, are connected is series. The space between the plates of one capacitor is filled with a dielectric material of dielectric constant K =4. Find the equivalent capacitacne of the system.
View SolutionHalf of the space between the plates of a parallel plate capacitor is filled with dielectric material of constant K. Then which of the plots are possible?
View SolutionAn uncharged parallel plate capacitor is connected to a battery. The electric field between the plates is 10V/m. Now a dielectric of dielectric constant 2 is inserted between the plates filling the entries space. The electric field between the plates now is
View SolutionThe terminals of a battery of emf V are connected to the two plates of a parallel plate capacitor. If the space between the plates of the capacitor is filled with an insulator of dielectric constant K, then :
View SolutionSeparation between the plates of a parallel plate capacitor is d and the area of each plates is A. When a slab of material of dielectric constant k and thickness t(t<d) is introduced between the plates. Its capacitance becomes
View SolutionThe capacitance of a capacitor becomes4/3 times its original value if a dielectric slab of thickness t=d/2 is inserted between the plates (d is the separation between the plates). What is the dielectric constant of the slab?
View SolutionThe capacitance of a capacitor between4/3 times its original value if a dielectric slab of thickness t=d/2 is inserted between the plates (d is the separation between the plates). What is the dielectric consant of the slab?
View SolutionThe capacitance of a capacitor between4/3 times its original value if a dielectric slab of thickness t=d/2 is inserted between the plates (d is the separation between the plates). What is the dielectric consant of the slab?
View SolutionFind the capacitance between A and B if two dielectric alabs (each of area A) of dielectric constants K1 and K2 and thicknesses d1 and d2 are inserted between the plates of a parallel plate capacitor of plate area A.
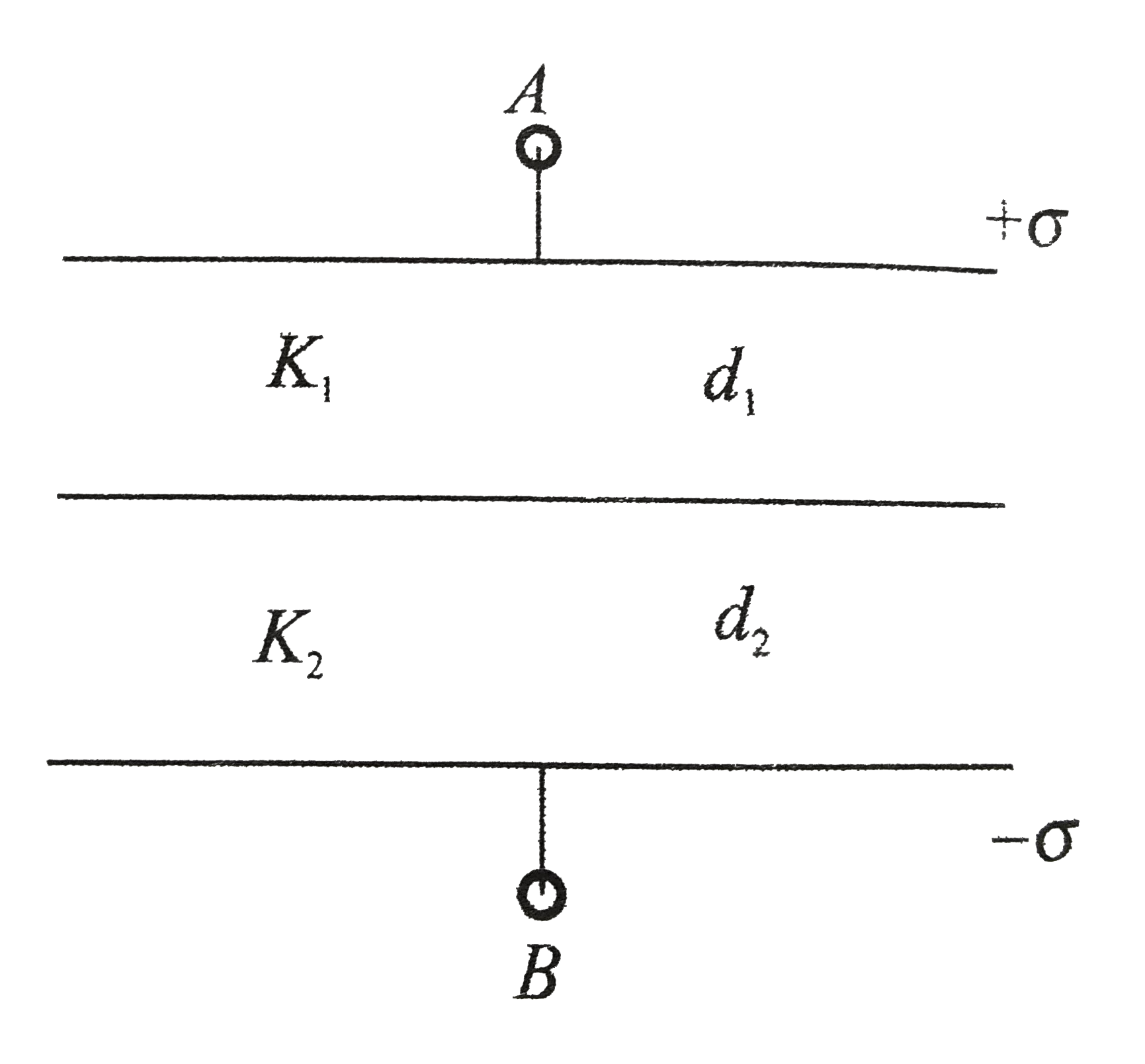 .
.
View SolutionA parallel plate capacitor has plate area of A separated by distance between them. It is completely filled with dielectric medium, its dielectric constant increases linearly as move from one plate to other plate from k1 to k2 . Then the capacitance of system is given by :
View Solution