A capacitor 1mF withstands a maximum voltage of 6KV while another capacitor 2mF withstands a maximum voltage of 4KV. If the capacitors are connected in series, the system will withstand a maximum voltage of
2KV
4KV
6KV
9KV
The correct Answer is:D
To solve the problem, we need to find the maximum voltage that the system of capacitors can withstand when they are connected in series. Here’s a step-by-step solution:
Step 1: Identify the given values
- Capacitor 1 (C1): 1 mF (1 millifarad) with a maximum voltage (V1) of 6 kV (6000 volts).
- Capacitor 2 (C2): 2 mF (2 millifarads) with a maximum voltage (V2) of 4 kV (4000 volts).
Step 2: Calculate the charge on each capacitor
The charge (Q) on a capacitor is given by the formula:
Q=C×V
For Capacitor 1 (C1):
Q1=C1×V1=(1×10−3F)×(6×103V)
Q1=6C
For Capacitor 2 (C2):
Q2=C2×V2=(2×10−3F)×(4×103V)
Q2=8C
Step 3: Determine the maximum charge in series
When capacitors are connected in series, the charge on each capacitor is the same. The maximum charge that the series combination can withstand is determined by the capacitor with the lower charge capacity. Here, since Q1<Q2:
Qmax=Q1=6C
Step 4: Calculate the equivalent capacitance for capacitors in series
The formula for the equivalent capacitance (C_eq) of capacitors in series is:
1Ceq=1C1+1C2
Substituting the values:
1Ceq=11×10−3+12×10−3
1Ceq=1000+500=1500
Ceq=11500=23×10−3F
Step 5: Calculate the maximum voltage across the equivalent capacitance
The maximum voltage (V_max) that the series combination can withstand is given by:
Vmax=QmaxCeq
Substituting the values:
Vmax=6C23×10−3F
Vmax=6×32×103
Vmax=9×103V
Vmax=9kV
Final Answer
The maximum voltage that the system can withstand when the capacitors are connected in series is 9 kV.
---
- Capacitor 1 (C1): 1 mF (1 millifarad) with a maximum voltage (V1) of 6 kV (6000 volts).
- Capacitor 2 (C2): 2 mF (2 millifarads) with a maximum voltage (V2) of 4 kV (4000 volts).
The charge (Q) on a capacitor is given by the formula:
Q=C×V
Q1=C1×V1=(1×10−3F)×(6×103V)
Q1=6C
Q2=C2×V2=(2×10−3F)×(4×103V)
Q2=8C
When capacitors are connected in series, the charge on each capacitor is the same. The maximum charge that the series combination can withstand is determined by the capacitor with the lower charge capacity. Here, since Q1<Q2:
Qmax=Q1=6C
The formula for the equivalent capacitance (C_eq) of capacitors in series is:
1Ceq=1C1+1C2
1Ceq=11×10−3+12×10−3
1Ceq=1000+500=1500
Ceq=11500=23×10−3F
The maximum voltage (V_max) that the series combination can withstand is given by:
Vmax=QmaxCeq
Vmax=6C23×10−3F
Vmax=6×32×103
Vmax=9×103V
Vmax=9kV
The maximum voltage that the system can withstand when the capacitors are connected in series is 9 kV.
Topper's Solved these Questions
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (CUTTENT ELECTRICITY )
108 Videos
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MOVING CHANGES & MEGNETISM)
95 Videos
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MAGNETISM AND MATTER )
52 Videos
- ALTERNATING CURRENTBOOK - AAKASH SERIESCHAPTER - ALTERNATING CURRENTEXERCISE - EXERCISE - III
24 Videos
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - LAW OF MOTION
128 Videos
Similar Questions
A capacitor of capacitance C1=1μF withstand a maximum voltage of V1=6KV, and another capacitor of capacitance C2=2μF, can with stand a maximum voltage of V2=4KV. If they are connected in series, what maximum voltage will the system withstand?
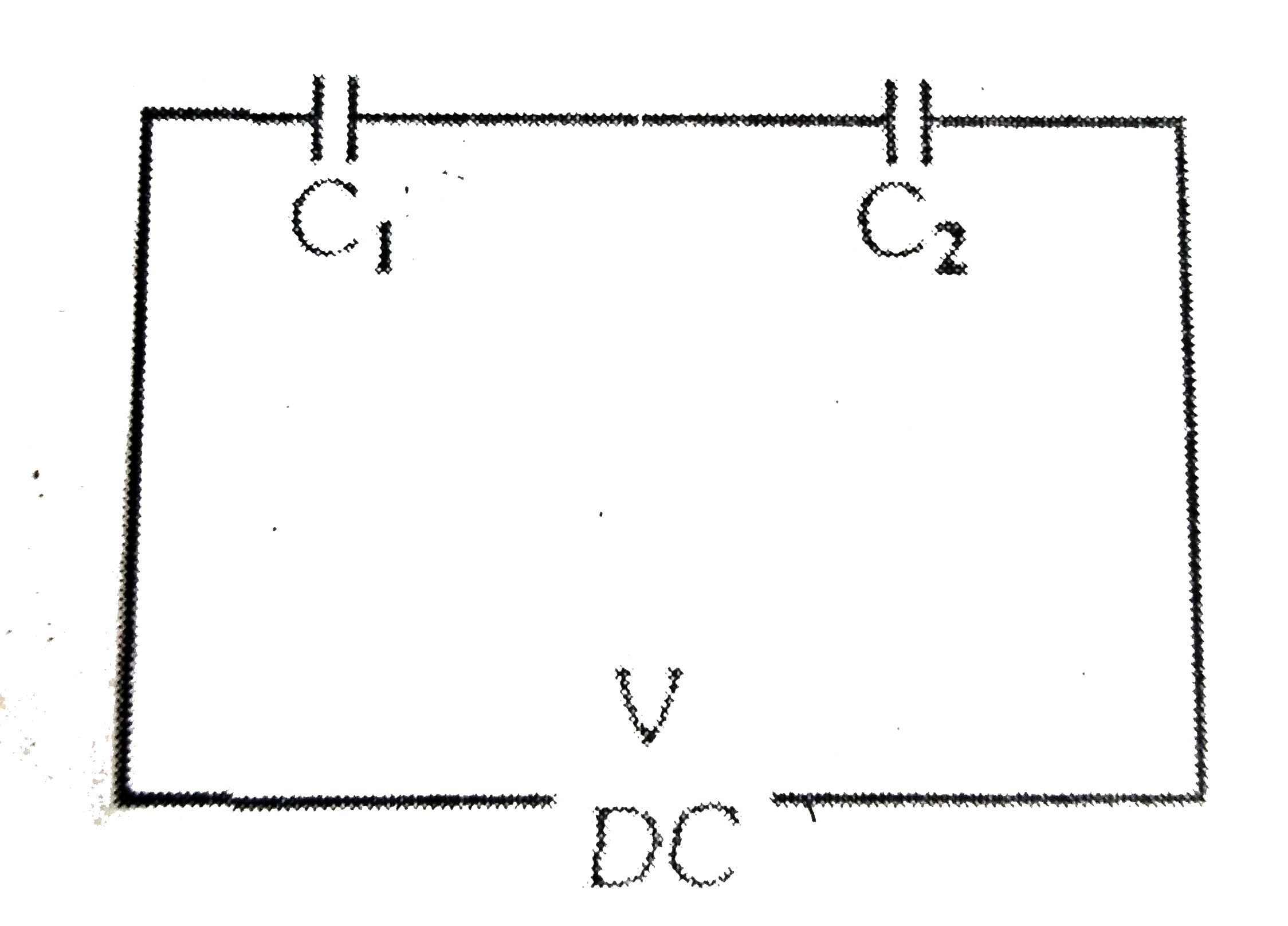
View SolutionA Capacitor of capacitance C1=1μF can withstand a maximum voltage V1=6.0 KV while another capacitor of capacitance C2=2.0μF withstands the maximum voltage V2=4.0 KV . What maximum will the system of these two capacitance withstand when connected in series as shown below .
View SolutionEffective capacitance of parallel combination of two capacitors C1andC2 is 10μF. When the capacitors are individually connected to a voltage source of 1V, the energy stored in the capacitor C2 is 4 times of C1. If these capacitors are connected in series, their effective capacitor will be: lt
View SolutionThree capacitors 2μF, 3μF and 5μF can withstand voltages to 3V,2V and 1V respectively. Their series combination can withstand a maximum voltage equal to
View SolutionA capaitor of capacitance C1=1.0μF withstands teh maximum voltage V1=6.0kV while a capacitor of capacitance Cs=2.0μF, the maximum voltage Vs=4.0kV. What voltage will the system of these two capacitors withsatand if they are connected in sereis ?
View SolutionA 2μF capacitor C1 is charge to a voltage 100 V and a 4μF capacitor C2 is charged to a voltage 50 V. The capacitors are then connected in parallel What is the loss of energy due to parallel connection?
View SolutionA 5−A wire can withstand a maximum power of 1W in circuit. The resistance of the fuse wire is
View SolutionA 5−A wire can withstand a maximum power of 1W in circuit. The resistance of the fuse wire is
View SolutionAn oscillator circuit contains an inductor 0.05 H and a capacitor of capacity 80μF. When the maximum voltage across the capacitor is 200 V, the maximum current (in amperes) in the circuit is
View SolutionA 1μF capacitor and a 2µF capacitor are connected in series across a 1200V supply line.
a. Find the charge on each capacitor and the voltage across them.
b. The charged capacitors are disconnected from the line and from each other and reconnected with terminals of like sign together. Find the final charge on each and the voltage across them.
View Solution
