To establish an instantaneous current of 2 A through a 1μFcapacitor, the potential difference across the capacitor plates should be changed at the rate of
2×104V/s
4×106V/s
2×106V/s
4×104V/s
The correct Answer is:C
To solve the problem, we need to find the rate of change of potential difference (dV/dt) across a capacitor when an instantaneous current of 2 A flows through it. We are given the capacitance of the capacitor as 1 µF (microfarad).
1. Understand the relationship between current, capacitance, and voltage:
The current (I) flowing through a capacitor is related to the capacitance (C) and the rate of change of voltage (dV/dt) across the capacitor by the formula:
I=CdVdt
2. Rearranging the formula:
To find the rate of change of voltage (dV/dt), we can rearrange the formula:
dVdt=IC
3. Substituting the known values:
We know:
- I=2A
- C=1μF=1×10−6F
Now substituting these values into the rearranged formula:
dVdt=2A1×10−6F
4. Calculating dV/dt:
Performing the calculation:
dVdt=2×106V/s
5. Conclusion:
Therefore, the potential difference across the capacitor plates should be changed at the rate of 2×106V/s.
Final Answer:
The rate of change of potential difference (dV/dt) is 2×106V/s.
The current (I) flowing through a capacitor is related to the capacitance (C) and the rate of change of voltage (dV/dt) across the capacitor by the formula:
I=CdVdt
To find the rate of change of voltage (dV/dt), we can rearrange the formula:
dVdt=IC
We know:
- I=2A
- C=1μF=1×10−6F
dVdt=2A1×10−6F
Performing the calculation:
dVdt=2×106V/s
Therefore, the potential difference across the capacitor plates should be changed at the rate of 2×106V/s.
The rate of change of potential difference (dV/dt) is 2×106V/s.
Topper's Solved these Questions
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (CUTTENT ELECTRICITY )
108 Videos
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MOVING CHANGES & MEGNETISM)
95 Videos
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MAGNETISM AND MATTER )
52 Videos
- ALTERNATING CURRENTBOOK - AAKASH SERIESCHAPTER - ALTERNATING CURRENTEXERCISE - EXERCISE - III
24 Videos
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - LAW OF MOTION
128 Videos
Similar Questions
Find charge on each capacitor and potential difference across each capacitor .

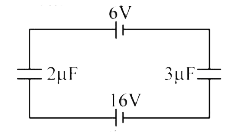
View SolutionWhat is the potential difference across 2μF capacitor in the circuit shown?
View SolutionThe displacement current flows in the dielectric of a capacitor when the potential difference across its plates-
View SolutionThe displacement current flows in the dielectric of a capacitor when the potential difference across its plates-
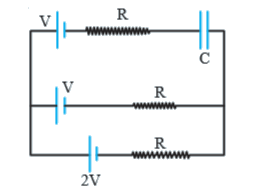
View SolutionIn the given circuit, with steady current, the potential difference across the capacitor is
View SolutionIn the arrangement shown in , the switch S is find
 the final potential difference across the 4μF capacitor
the final potential difference across the 4μF capacitor
View SolutionIn the given circuit, with steady current, calculate the potential difference across the capacitor and the charge stored in it.
View SolutionTwo capacitors of capacitance 2μF and 3μF respectively are charged to potential difference 20 V and 40 V respectively. Now the capacitors are connected in series with a resistance such that the positively charged plate of one capacitor is connected to the positively charged plate of the other. The initial current through the resistance is I0. The potential difference across the 2μF capacitor at the instant the current has reduced to I02 is_______ V.
View SolutionTwo identical parallel plate capacitors are connected in series and then joined in series with a battery of 100V. A slab of dielectric constant K=3 is inserted between the plates of the first capacitor. Then, the potential difference across the capacitor will be, respectively.
View SolutionA capacitance C, a resistance R and an emf (ε)are connected in series at t=0.What is the maximum value of (a) the potential difference across the resistor, (b) the current in the circuit,(c )the potential difference across the capacitor, (d) the energy stored in the capacitor ,(e)the power delivered by the battery and (f) the power converted int heat.
View Solution
