Three capacitances, each of 3μF , are provided. These cannot be combined to provide the resultant capacitance of:
1μF
2μF
6μF
4.5μF
The correct Answer is:C
To solve the problem, we need to analyze the combinations of three capacitors, each with a capacitance of 3μF, and determine the resultant capacitance for different configurations. The goal is to find out which of the given options cannot be achieved as a resultant capacitance.
1. Identify the Given Capacitors:
We have three capacitors:
- C1=3μF
- C2=3μF
- C3=3μF
2. Calculate Resultant Capacitance in Series:
When capacitors are connected in series, the formula for the resultant capacitance C is:
1C=1C1+1C2+1C3
Substituting the values:
1C=13+13+13=33=1
Therefore,
C=1μF
This means a resultant capacitance of 1μF is possible.
3. Calculate Resultant Capacitance with Two in Parallel and One in Series:
Let's take C1 and C2 in parallel and C3 in series:
- The equivalent capacitance of C1 and C2 in parallel is:
C′=C1+C2=3+3=6μF
- Now, C′ is in series with C3:
1C=1C′+1C3=16+13
1C=16+26=36=12
Thus,
C=2μF
This means a resultant capacitance of 2μF is also possible.
4. Calculate Resultant Capacitance with Two in Series and One in Parallel:
Now, let’s take C1 and C2 in series and C3 in parallel:
- The equivalent capacitance of C1 and C2 in series is:
1C′=1C1+1C2=13+13=23
Thus,
C′=32μF
- Now, C′ is in parallel with C3:
C=C′+C3=32+3=32+62=92=4.5μF
This means a resultant capacitance of 4.5μF is also possible.
5. Conclusion:
The possible resultant capacitances from the combinations are:
- 1μF
- 2μF
- 4.5μF
The only capacitance that cannot be achieved with the given capacitors is:
- 6μF
Final Answer:
The capacitance that cannot be combined to provide the resultant capacitance is 6 μF.
We have three capacitors:
- C1=3μF
- C2=3μF
- C3=3μF
When capacitors are connected in series, the formula for the resultant capacitance C is:
1C=1C1+1C2+1C3
Substituting the values:
1C=13+13+13=33=1
Therefore,
C=1μF
This means a resultant capacitance of 1μF is possible.
Let's take C1 and C2 in parallel and C3 in series:
- The equivalent capacitance of C1 and C2 in parallel is:
C′=C1+C2=3+3=6μF
- Now, C′ is in series with C3:
1C=1C′+1C3=16+13
1C=16+26=36=12
Thus,
C=2μF
This means a resultant capacitance of 2μF is also possible.
Now, let’s take C1 and C2 in series and C3 in parallel:
- The equivalent capacitance of C1 and C2 in series is:
1C′=1C1+1C2=13+13=23
Thus,
C′=32μF
- Now, C′ is in parallel with C3:
C=C′+C3=32+3=32+62=92=4.5μF
This means a resultant capacitance of 4.5μF is also possible.
The possible resultant capacitances from the combinations are:
- 1μF
- 2μF
- 4.5μF
The only capacitance that cannot be achieved with the given capacitors is:
- 6μF
The capacitance that cannot be combined to provide the resultant capacitance is 6 μF.
Topper's Solved these Questions
- APPENDICES ( REVISION EXERCISE )Book:AAKASH SERIESChapter:APPENDICES ( REVISION EXERCISE )Exercise:REVISION EXERCISE (CUTTENT ELECTRICITY )
Explore 108 Videos
- APPENDICES ( REVISION EXERCISE )Book:AAKASH SERIESChapter:APPENDICES ( REVISION EXERCISE )Exercise:REVISION EXERCISE (MOVING CHANGES & MEGNETISM)
Explore 95 Videos
- APPENDICES ( REVISION EXERCISE )Book:AAKASH SERIESChapter:APPENDICES ( REVISION EXERCISE )Exercise:REVISION EXERCISE (MAGNETISM AND MATTER )
Explore 52 Videos
- ALTERNATING CURRENTBook:AAKASH SERIESChapter:ALTERNATING CURRENTExercise:EXERCISE - III
Explore 24 Videos
- APPENDICES (REVISION EXERCISE)Book:AAKASH SERIESChapter:APPENDICES (REVISION EXERCISE)Exercise:LAW OF MOTION
Explore 128 Videos
Similar Questions
Find the resultant capacitance along AB
View SolutionThe resultant capacitance of given circuit is
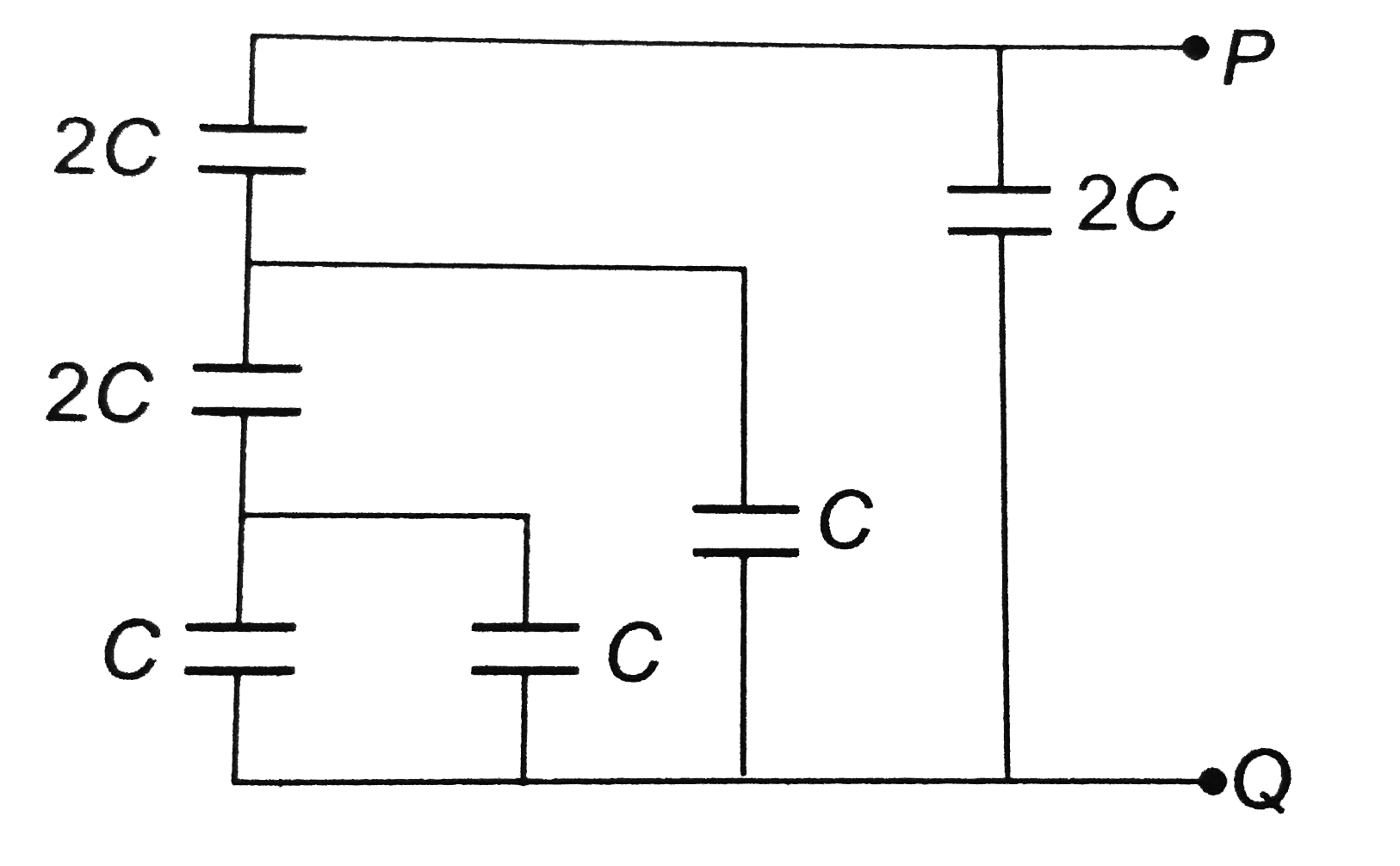
View SolutionSeven capacitors each of capacitance 2μF are to be connected in a configuration to obtain an effective capacitance of (1011)μF. Which of the combination (s) shown in figure will achieve the desired result?
View SolutionThree capacitors each of capacitance 9 pF are connected in series. What is the total capacitance of the combination ?
View SolutionIn the figure, a capacitor is field with dielectrics. The resultant capacitance is

View SolutionThree condensers each of capacitance 2F are put in series. The resultant capacitance is
View SolutionIn the arrangement of the capacitor shown in the figure, each C1 capacitor has capacitance of 3μF and each C2 capacitor has capacitance of 2μF then,
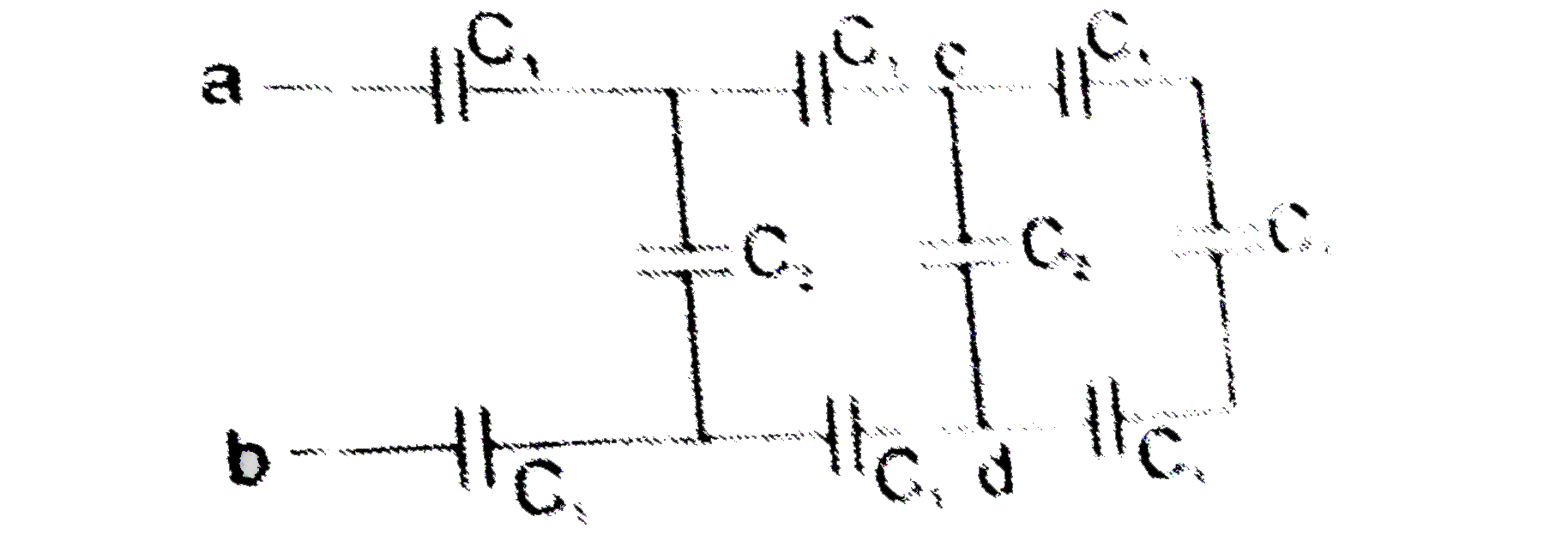
(i) Equivalent capacitance of the network between the points a and b is :
View SolutionThree capacitors of capacitance 2pF,3pFand4pF are connected in parallel. (a) what is the total capacitance of the combination ? (b) Determine the charge on each capacitor, If the combination is connected to 100V supply.
View SolutionAn infinite number of identical capacitors each of capacitance 1mF are connected as shown in the figure. Then the equivalent capacitance between A and B is.
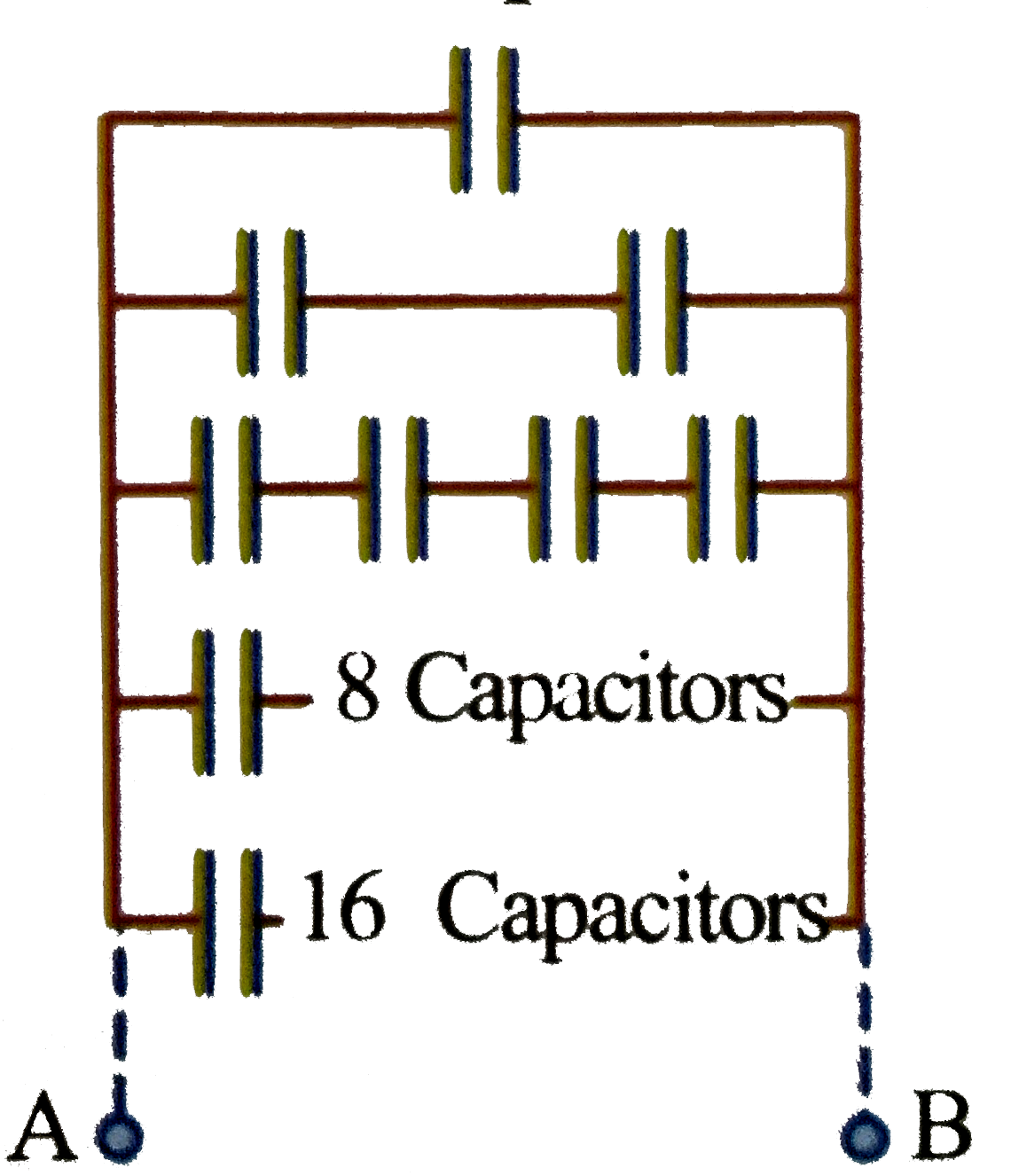 .
.
View SolutionAn infinite number of identical capacitors each of capacitance 1mF are connected as shown in the figure. Then the equivalent capacitance between A and B is.
 .
.
View Solution