Seven capacitors each of capacitance 2μF are to be connected in a configuration to obtain an effective capacitance of (1011)μF. Which of the combination (s) shown in figure will achieve the desired result?
2 in parallel, 5 in series
3 in parallel, 4 in series.
4 in parallel, 3 in series
5 in parallel, 2 in series
The correct Answer is:D
To solve the problem of determining which configuration of capacitors will yield an effective capacitance of 1011μF, we will analyze each option step by step.
Given:
- Seven capacitors, each with a capacitance of 2μF.
- Desired effective capacitance: 1011μF.
Step 1: Analyze Each Configuration
Option 1: 2 in Parallel and 5 in Series
1. Calculate the equivalent capacitance of the two capacitors in parallel:
Ceq,parallel=C1+C2=2μF+2μF=4μF
2. Calculate the equivalent capacitance of the five capacitors in series:
Ceq,series=Cn=2μF5=0.4μF
3. Combine the two results (parallel and series):
Ceq,total=Ceq,parallel⋅Ceq,seriesCeq,parallel+Ceq,series=4μF⋅0.4μF4μF+0.4μF=1.64.4μF=822μF=411μF
- This is not equal to 1011μF.
Option 2: 3 in Parallel and 4 in Series
1. Calculate the equivalent capacitance of the three capacitors in parallel:
Ceq,parallel=2μF+2μF+2μF=6μF
2. Calculate the equivalent capacitance of the four capacitors in series:
Ceq,series=Cn=2μF4=0.5μF
3. Combine the two results:
Ceq,total=Ceq,parallel⋅Ceq,seriesCeq,parallel+Ceq,series=6μF⋅0.5μF6μF+0.5μF=36.5μF=613μF
- This is not equal to 1011μF.
Option 3: 4 in Parallel and 3 in Series
1. Calculate the equivalent capacitance of the four capacitors in parallel:
Ceq,parallel=2μF+2μF+2μF+2μF=8μF
2. Calculate the equivalent capacitance of the three capacitors in series:
Ceq,series=Cn=2μF3≈0.6667μF
3. Combine the two results:
Ceq,total=Ceq,parallel⋅Ceq,seriesCeq,parallel+Ceq,series=8μF⋅0.6667μF8μF+0.6667μF≈5.33368.6667μF≈0.615μF
- This is not equal to 1011μF.
Option 4: 5 in Parallel and 2 in Series
1. Calculate the equivalent capacitance of the five capacitors in parallel:
Ceq,parallel=2μF+2μF+2μF+2μF+2μF=10μF
2. Calculate the equivalent capacitance of the two capacitors in series:
Ceq,series=Cn=2μF2=1μF
3. Combine the two results:
Ceq,total=Ceq,parallel⋅Ceq,seriesCeq,parallel+Ceq,series=10μF⋅1μF10μF+1μF=1011μF
- This matches the desired effective capacitance.
Conclusion
The correct configuration to achieve an effective capacitance of 1011μF is Option 4: 5 capacitors in parallel and 2 capacitors in series.
- Seven capacitors, each with a capacitance of 2μF.
- Desired effective capacitance: 1011μF.
1. Calculate the equivalent capacitance of the two capacitors in parallel:
Ceq,parallel=C1+C2=2μF+2μF=4μF
2. Calculate the equivalent capacitance of the five capacitors in series:
Ceq,series=Cn=2μF5=0.4μF
Ceq,total=Ceq,parallel⋅Ceq,seriesCeq,parallel+Ceq,series=4μF⋅0.4μF4μF+0.4μF=1.64.4μF=822μF=411μF
- This is not equal to 1011μF.
1. Calculate the equivalent capacitance of the three capacitors in parallel:
Ceq,parallel=2μF+2μF+2μF=6μF
Ceq,series=Cn=2μF4=0.5μF
Ceq,total=Ceq,parallel⋅Ceq,seriesCeq,parallel+Ceq,series=6μF⋅0.5μF6μF+0.5μF=36.5μF=613μF
- This is not equal to 1011μF.
1. Calculate the equivalent capacitance of the four capacitors in parallel:
Ceq,parallel=2μF+2μF+2μF+2μF=8μF
Ceq,series=Cn=2μF3≈0.6667μF
Ceq,total=Ceq,parallel⋅Ceq,seriesCeq,parallel+Ceq,series=8μF⋅0.6667μF8μF+0.6667μF≈5.33368.6667μF≈0.615μF
- This is not equal to 1011μF.
1. Calculate the equivalent capacitance of the five capacitors in parallel:
Ceq,parallel=2μF+2μF+2μF+2μF+2μF=10μF
Ceq,series=Cn=2μF2=1μF
Ceq,total=Ceq,parallel⋅Ceq,seriesCeq,parallel+Ceq,series=10μF⋅1μF10μF+1μF=1011μF
- This matches the desired effective capacitance.
The correct configuration to achieve an effective capacitance of 1011μF is Option 4: 5 capacitors in parallel and 2 capacitors in series.
Topper's Solved these Questions
- CAPACITOR AND CAPACITANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Multile Correct
11 Videos
- CAPACITOR AND CAPACITANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Comprhension
35 Videos
- CAPACITOR AND CAPACITANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Subjective
24 Videos
- ATOMIC PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - ddp.4.3
15 Videos
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type
51 Videos
Similar Questions
Seven capacitors, each a of a cpacitance 2μF, are to be connected in a configuration to obatin an effective capacitance of (1613)μF. Which of the combinations, shown in figure below, will achieve the desired value ?
View SolutionThree capacitors each of capacity 4μF are to be connected in such a way that the effective capacitance is 6μF. This can be done by
View Solution
Knowledge Check
Three capacitors each of capacity 4μF are to be connected in such a way that the effective capacitance is 6μF. This can be done by
Aconnecting them in seriesBconnecting them is parallelCconnecting two in series and one in parallelDconnecting two in parallel and one is series
Three capacitors each of capacity 4μF are to be connected in such a way that the effective capacitance is 6μF. This can be done by
View SolutionThree capacitors of capacitance 3μF are connected in a circuit. Then, their maximum and minimum capacitance will be
View SolutionSix equal capacitors each of capacitance 10μF are connect as shown in the figure. Then the equivalent capacitance between A and B is
View SolutionSome capacitors each of capacitance 30μF are connected as shown in. Calculate the equivalent capacitance between terminals A and B
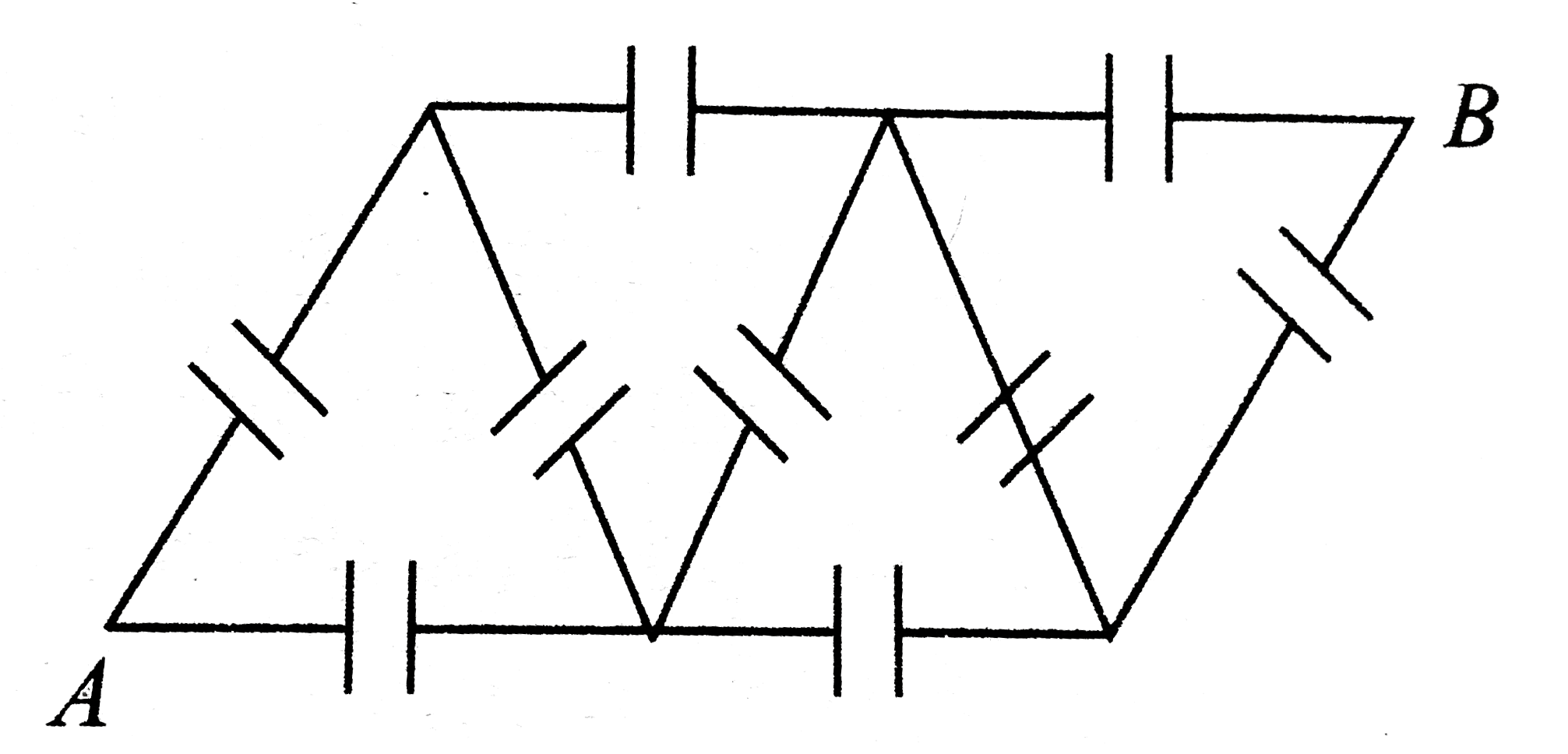 .
.
View SolutionSix identical capacitors each of capacitance 2μF are connected as shown below. The equivalent capacitance between the points A and B is
View SolutionSix equal capacitors each of capacitance C are connected as shown in the figure. The equivalent capacitance between points A and B is
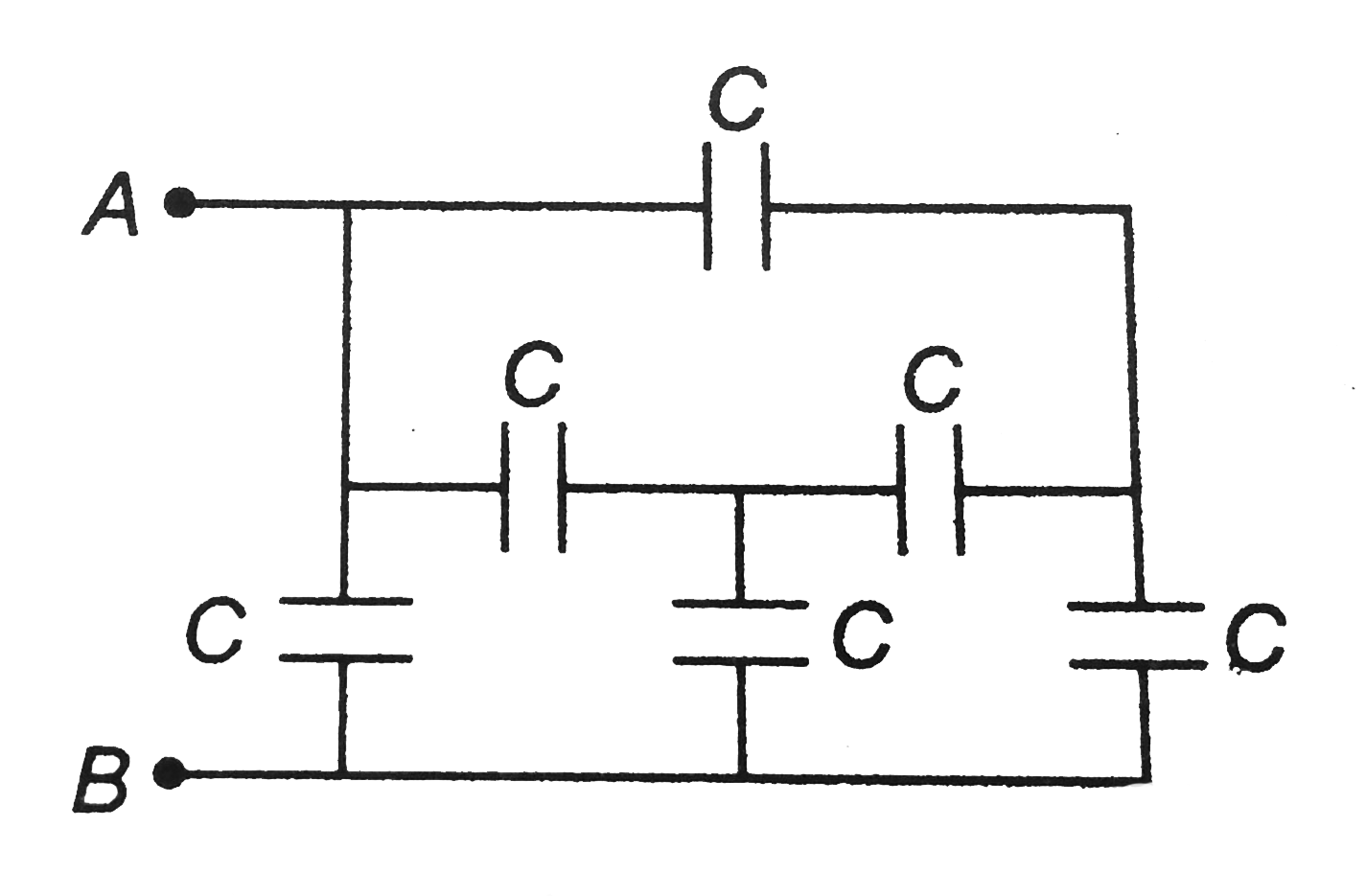
View SolutionThree equal capacitors, each with capacitance C are connected as shown in figure. Then the equivalent capacitance between A and B is
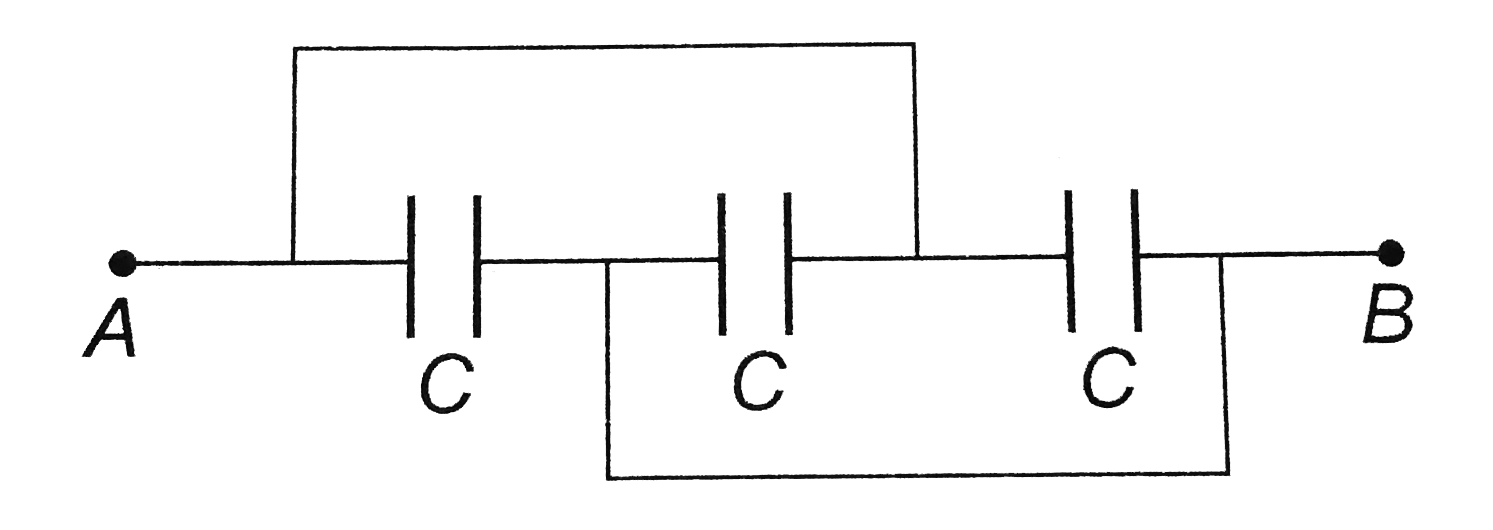
View Solution


