Three capacitors each of capacity 4μF are to be connected in such a way that the effective capacitance is 6μF. This can be done by
connecting all of them in series
connecting them in parallel
connecting two in series and one in parallel
connecting two in parallel and one in series
The correct Answer is:C
To solve the problem of finding how to connect three capacitors, each of capacity 4μF, to achieve an effective capacitance of 6μF, we can analyze the different configurations of connecting capacitors: series and parallel.
1. Identify the Capacitor Values:
Each capacitor has a capacitance of C=4μF.
2. Understand the Effective Capacitance for Series and Parallel:
- For capacitors in series:
1Ceq=1C1+1C2+1C3
For three identical capacitors, this simplifies to:
Ceq=C3
- For capacitors in parallel:
Ceq=C1+C2+C3
For three identical capacitors, this simplifies to:
Ceq=3C
3. Evaluate Each Option:
- Option A: All capacitors in series.
Ceq=4μF3≈1.33μF(Not 6μF)
- Option B: All capacitors in parallel.
Ceq=4μF+4μF+4μF=12μF(Not 6μF)
- Option C: Two capacitors in series and one in parallel.
- First, calculate the equivalent of the two capacitors in series:
Cseries=4μF⋅4μF4μF+4μF=168=2μF
- Now add the third capacitor in parallel:
Ceq=Cseries+C3=2μF+4μF=6μF(This is correct)
- Option D: Two capacitors in parallel and one in series.
- First, calculate the equivalent of the two capacitors in parallel:
Cparallel=4μF+4μF=8μF
- Now calculate the equivalent with the third capacitor in series:
1Ceq=1Cparallel+1C3=18μF+14μF
1Ceq=18+28=38⇒Ceq=83≈2.67μF(Not 6μF)
4. Conclusion:
The only configuration that gives an effective capacitance of 6μF is Option C: connecting two capacitors in series and one in parallel.
Each capacitor has a capacitance of C=4μF.
- For capacitors in series:
1Ceq=1C1+1C2+1C3
For three identical capacitors, this simplifies to:
Ceq=C3
- For capacitors in parallel:
Ceq=C1+C2+C3
For three identical capacitors, this simplifies to:
Ceq=3C
- Option A: All capacitors in series.
Ceq=4μF3≈1.33μF(Not 6μF)
- Option B: All capacitors in parallel.
Ceq=4μF+4μF+4μF=12μF(Not 6μF)
- Option C: Two capacitors in series and one in parallel.
- First, calculate the equivalent of the two capacitors in series:
Cseries=4μF⋅4μF4μF+4μF=168=2μF
- Now add the third capacitor in parallel:
Ceq=Cseries+C3=2μF+4μF=6μF(This is correct)
- Option D: Two capacitors in parallel and one in series.
- First, calculate the equivalent of the two capacitors in parallel:
Cparallel=4μF+4μF=8μF
- Now calculate the equivalent with the third capacitor in series:
1Ceq=1Cparallel+1C3=18μF+14μF
1Ceq=18+28=38⇒Ceq=83≈2.67μF(Not 6μF)
The only configuration that gives an effective capacitance of 6μF is Option C: connecting two capacitors in series and one in parallel.
Similar Questions
Seven capacitors each of capacitance 2μF are to be connected in a configuration to obtain an effective capacitance of (1011)μF. Which of the combination (s) shown in figure will achieve the desired result?
View SolutionSeven capacitors, each a of a cpacitance 2μF, are to be connected in a configuration to obatin an effective capacitance of (1613)μF. Which of the combinations, shown in figure below, will achieve the desired value ?
View SolutionThe effective capacitence in μF in between A and B will be
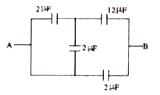
View SolutionSome capacitors each of capacitance 30μF are connected as shown in. Calculate the equivalent capacitance between terminals A and B
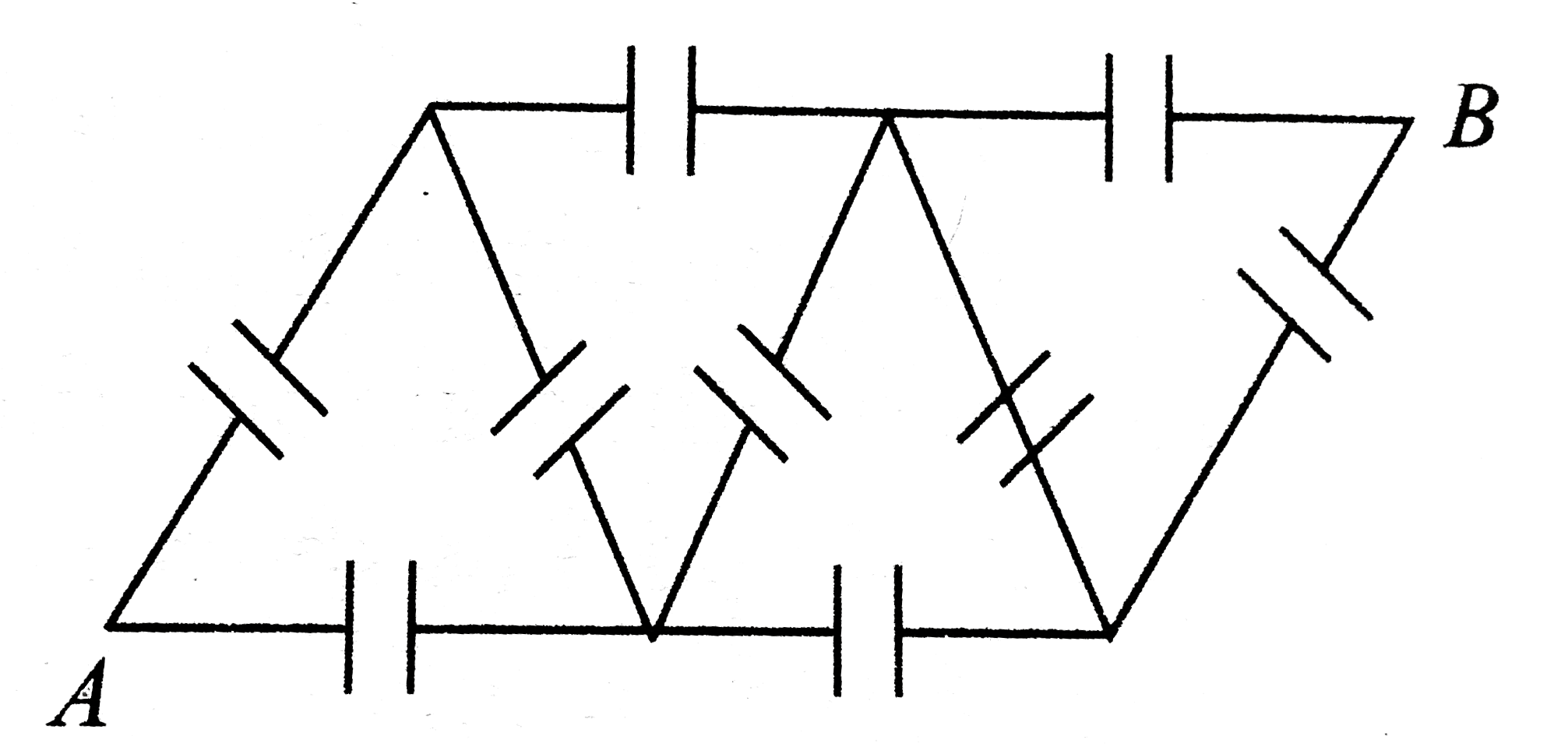 .
.
View SolutionThree capacitors 2μF,3μFand6μF are joined with each other. What is the minimum effective capacitance?
View SolutionThree capacitors of capacitance 3μF are connected in a circuit. Then, their maximum and minimum capacitance will be
View SolutionFour capacitors each of capacity 8μF area connected with each other as shown in figure. The equivalent capacitance between points X and Y will be

View SolutionSix identical capacitors each of capacitance 2μF are connected as shown below. The equivalent capacitance between the points A and B is
View SolutionFour capacitors of each of capacity 3μF are connected as shown in the adjoining figure. The ratio of equivalent capacitance between A and B and between A and C will be

View SolutionSix equal capacitors each of capacitance 10μF are connect as shown in the figure. Then the equivalent capacitance between A and B is
View Solution


