Two identical parallel plate capacitors are connected in series and then joined in series with a battery of 100V. A slab of dielectric constant K=3 is inserted between the plates of the first capacitor. Then, the potential difference across the capacitor will be, respectively.
25V,75V
75V,25V
20V,80V
50V,50V
The correct Answer is:A
To solve the problem step by step, we will analyze the circuit with two identical parallel plate capacitors connected in series, where one capacitor has a dielectric slab inserted.
Step 1: Understand the System
We have two identical capacitors, C1 and C2, connected in series to a 100 V battery. A dielectric slab with a dielectric constant K=3 is inserted into the first capacitor (C1).
Step 2: Determine the Capacitance of the Capacitors
The capacitance of a capacitor without a dielectric is given by:
C=ε0Ad
When a dielectric is inserted, the capacitance of the first capacitor (C1) becomes:
C1=K⋅C=3C
The second capacitor (C2) remains unchanged:
C2=C
Step 3: Calculate the Total Capacitance in Series
For capacitors in series, the total capacitance Ctotal is given by:
1Ctotal=1C1+1C2
Substituting the values:
1Ctotal=13C+1C
Finding a common denominator:
1Ctotal=1+33C=43C
Thus, the total capacitance is:
Ctotal=3C4
Step 4: Calculate the Total Charge in the Circuit
The total charge Q stored in the capacitors when connected to the battery is:
Q=Ctotal⋅V=3C4⋅100
Q=75C
Step 5: Calculate the Voltage Across Each Capacitor
The voltage across each capacitor can be calculated using the formula V=QC.
For the first capacitor (C1):
VC1=QC1=75C3C=25V
For the second capacitor (C2):
VC2=QC2=75CC=75V
Step 6: Conclusion
The potential difference across the first capacitor (with dielectric) is 25 V, and across the second capacitor is 75 V. Therefore, the final answer is:
VC1=75V,VC2=25V
Final Answer
The potential difference across the capacitors will be, respectively, 75V and 25V.
---
We have two identical capacitors, C1 and C2, connected in series to a 100 V battery. A dielectric slab with a dielectric constant K=3 is inserted into the first capacitor (C1).
The capacitance of a capacitor without a dielectric is given by:
C=ε0Ad
When a dielectric is inserted, the capacitance of the first capacitor (C1) becomes:
C1=K⋅C=3C
The second capacitor (C2) remains unchanged:
C2=C
For capacitors in series, the total capacitance Ctotal is given by:
1Ctotal=1C1+1C2
Substituting the values:
1Ctotal=13C+1C
Finding a common denominator:
1Ctotal=1+33C=43C
Thus, the total capacitance is:
Ctotal=3C4
The total charge Q stored in the capacitors when connected to the battery is:
Q=Ctotal⋅V=3C4⋅100
Q=75C
The voltage across each capacitor can be calculated using the formula V=QC.
VC1=QC1=75C3C=25V
VC2=QC2=75CC=75V
The potential difference across the first capacitor (with dielectric) is 25 V, and across the second capacitor is 75 V. Therefore, the final answer is:
VC1=75V,VC2=25V
The potential difference across the capacitors will be, respectively, 75V and 25V.
Topper's Solved these Questions
- CAPACITOR AND CAPACITANCEBook:CENGAGE PHYSICS ENGLISHChapter:CAPACITOR AND CAPACITANCEExercise:Multile Correct
Explore 11 Videos
- CAPACITOR AND CAPACITANCEBook:CENGAGE PHYSICS ENGLISHChapter:CAPACITOR AND CAPACITANCEExercise:Comprhension
Explore 35 Videos
- CAPACITOR AND CAPACITANCEBook:CENGAGE PHYSICS ENGLISHChapter:CAPACITOR AND CAPACITANCEExercise:Subjective
Explore 24 Videos
- ATOMIC PHYSICSBook:CENGAGE PHYSICS ENGLISHChapter:ATOMIC PHYSICSExercise:ddp.4.3
Explore 15 Videos
- CENGAGE PHYSICS DPPBook:CENGAGE PHYSICS ENGLISHChapter:CENGAGE PHYSICS DPPExercise:subjective type
Explore 51 Videos
Similar Questions
Two identical parallel plate capacitors are connected in series to a battery of 100V. A dielectric slab of dielectric constant 4.0 is inserted between the plates of second capacitor. The potential difference across the capacitors will now be respectively
View SolutionA dielectric slab is inserted between the plates of an isolated capacitor. The force between the plates will
View SolutionA capacitor and a bulb are connected in series with a source of alternating emf. If a dielectric slab is inserted between the plates of the capacitor, then
View SolutionTwo identical parallel plate capacitors are connected in series to a battery of 100N . A dielectric slab of dielectric constant 4.0 is inserted between the plates of second capacitor. The potential difference across the capaitors will now be respectively.
View SolutionTwo identical capacitors A and B shown in the given circuit are joined in series with a battery. If a dielectric slab of dielectric constant K is slipped between the plates of capacitor B and battery remains connected, then the energy of capacitor A will-

View SolutionA parallel plate capacitor of capacitance 90 pF is connected to a battery of emf 20 V. If a dielectric material of dielectric constant K=53 is inserted between the plates, the magnitude of the induced charge will be :
View SolutionA parallel capacitor of capacitance C is charged and disconnected from the battery. The energy stored in it is E. If a dielectric slab of dielectric constant 6 is inserted between the plates of the capacitor then energy and capacitance will become.
View SolutionThe potential enery of a charged parallel plate capacitor is U0. If a slab of dielectric constant K is inserted between the plates, then the new potential energy will be
View SolutionThe potential enery of a charged parallel plate capacitor is U0. If a slab of dielectric constant K is inserted between the plates, then the new potential energy will be
View SolutionWhen a dielectric slab is inserted between the plates of one of the two identical capacitors shown in the figure then match the following:
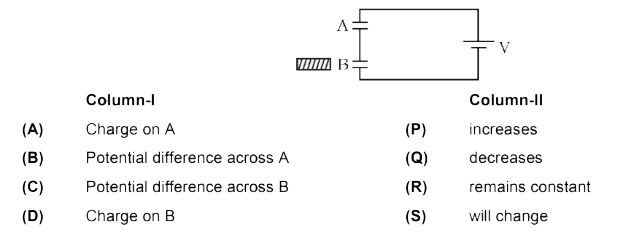
View Solution