Three identical capacitors, each of capacitance , are connected in series with a battery of emf and get fully charged. Now the battery is removed and the capacitors are cannected in parallel with positive terminals at one point and negative terminals at other point. Then, The connon potintial will be.
zero
The correct Answer is:C
To solve the problem step by step, let's break it down:
Step 1: Understand the Initial Configuration
Three identical capacitors, each with capacitance C, are connected in series to a battery with an emf V.
Step 2: Calculate the Equivalent Capacitance in Series
When capacitors are connected in series, the equivalent capacitance Ceq can be calculated using the formula:
1Ceq=1C1+1C2+1C3
Since all capacitors are identical and have capacitance C:
1Ceq=1C+1C+1C=3C⟹Ceq=C3
Step 3: Calculate the Charge on the Capacitors
The charge Q on the equivalent capacitor when connected to the battery is given by:
Q=Ceq⋅V=(C3)⋅V=CV3
Since the charge is the same on each capacitor in series, each capacitor will have a charge Q=CV3.
Step 4: Determine the Voltage Across Each Capacitor
The voltage across each capacitor V′ can be calculated using the formula:
V′=QC=CV3C=V3
Thus, each capacitor has a voltage of V3.
Step 5: Disconnect the Battery and Connect Capacitors in Parallel
After charging, the battery is removed, and the capacitors are connected in parallel. In a parallel connection, the voltage across each capacitor remains the same.
Step 6: Calculate the Common Potential in Parallel
When the capacitors are connected in parallel, the common potential Vcommon will be the same across all capacitors. Since each capacitor was charged to V3, the common potential will also be:
Vcommon=V3
Final Answer
The common potential when the capacitors are connected in parallel is:
V3
Three identical capacitors, each with capacitance C, are connected in series to a battery with an emf V.
When capacitors are connected in series, the equivalent capacitance Ceq can be calculated using the formula:
1Ceq=1C1+1C2+1C3
Since all capacitors are identical and have capacitance C:
1Ceq=1C+1C+1C=3C⟹Ceq=C3
The charge Q on the equivalent capacitor when connected to the battery is given by:
Q=Ceq⋅V=(C3)⋅V=CV3
Since the charge is the same on each capacitor in series, each capacitor will have a charge Q=CV3.
The voltage across each capacitor V′ can be calculated using the formula:
V′=QC=CV3C=V3
Thus, each capacitor has a voltage of V3.
After charging, the battery is removed, and the capacitors are connected in parallel. In a parallel connection, the voltage across each capacitor remains the same.
When the capacitors are connected in parallel, the common potential Vcommon will be the same across all capacitors. Since each capacitor was charged to V3, the common potential will also be:
Vcommon=V3
The common potential when the capacitors are connected in parallel is:
V3
Topper's Solved these Questions
- CAPACITOR AND CAPACITANCEBook:CENGAGE PHYSICS ENGLISHChapter:CAPACITOR AND CAPACITANCEExercise:Multile Correct
Explore 11 Videos
- CAPACITOR AND CAPACITANCEBook:CENGAGE PHYSICS ENGLISHChapter:CAPACITOR AND CAPACITANCEExercise:Comprhension
Explore 35 Videos
- CAPACITOR AND CAPACITANCEBook:CENGAGE PHYSICS ENGLISHChapter:CAPACITOR AND CAPACITANCEExercise:Subjective
Explore 24 Videos
- ATOMIC PHYSICSBook:CENGAGE PHYSICS ENGLISHChapter:ATOMIC PHYSICSExercise:ddp.4.3
Explore 15 Videos
- CENGAGE PHYSICS DPPBook:CENGAGE PHYSICS ENGLISHChapter:CENGAGE PHYSICS DPPExercise:subjective type
Explore 51 Videos
Similar Questions
Three capacitors of capacitance C1=3μf,C2=6μfandC3=10μf, are connected to a 10V battery as shown in Figure 3 below
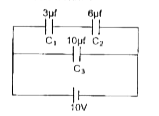
Calculate:
Equivalent capacitance
View SolutionTwo capacitors A and B are connected in series with a battery as shown in the figure. When the switch S is closed and the two capacitors get charged fully, then

View SolutionTwo capacitors A and B are connected in series with a battery as shown in the figure. When the switch S is closed and the two capacitors get charged fully, then

View SolutionTwo capacitors A and B are connected in series with a battery as shown in the figure. When the switch S is closed and the two capacitors get charged fully, then

View SolutionIn series connection of cells, positive terminals of all cells are connected to one point and negative terminals of all cells to other point.
View SolutionTwo identical capacitor C1 and C2 are connected in series with a battery. They are fully charged. Now a dielectric slab is inserted between the plates of C2. The potential across C1 will :

View SolutionA parallel plate capacitor of capacitance C is connected to a battery and is charged to a potential difference V. Another capacitor of capacitance 2C is ismilarly charged to a potential difference 2V. The charging battery is now disconnected and the capacitors are connected in parallel to each other in such a way that the poistive terminal of one is connected to the negative terminal of the other. The final energy of the configuration is
View SolutionA capacitor of 60 pF charged to 20 volt. Now battery is removed and then this capacitor is connected to another identical uncharged capacitor. Find heat loss in nJ
View SolutionA capacitor of 60 pF charged to 20 volt. Now battery is removed and then this capacitor is connected to another identical uncharged capacitor. Find heat loss in nJ
View SolutionThe parallel combination of two air filled parallel plate capacitor of capacitance C and nC is connected to a battery of voltage, V. When the capacitors are fulley charged, the battery is removed and after that a dielectric material of dielectric constant K is placed between the two plates of the first capacitors. the new potential difference of the combined system is
View Solution
