Three equal charges q1,q2,q3 are placed at the three corners ABC of a square ABCD. If the force between the charges at A and B (on q1andq2) is F12 and that between A and C is F13 then the ratio of magnitudes F12 and F13 is
1/2
2
11/√2
√2
The correct Answer is:B
To solve the problem of finding the ratio of the magnitudes of the forces F12 and F13 between three equal charges placed at the corners of a square, we can follow these steps:
Step 1: Understand the Configuration
We have three equal charges q1,q2, and q3 placed at the corners A, B, and C of a square ABCD. The distances between the charges are determined by the geometry of the square.
Step 2: Identify the Distances
Let the side length of the square be a.
- The distance between charges at A and B (i.e., F12) is equal to the side of the square: dAB=a.
- The distance between charges at A and C (i.e., F13) is the diagonal of the square: dAC=√2a.
Step 3: Calculate the Forces
Using Coulomb's Law, the force between two point charges is given by:
F=kq1q2r2
where k is Coulomb's constant.
Calculate F12:
F12=kq1q2d2AB=kq2a2
Calculate F13:
F13=kq1q3d2AC=kq2(√2a)2=kq22a2
Step 4: Find the Ratio F12F13
Now we can find the ratio of the magnitudes of the forces:
F12F13=kq2a2kq22a2=112=2
Final Answer
Thus, the ratio of the magnitudes F12 and F13 is:
F12F13=2
We have three equal charges q1,q2, and q3 placed at the corners A, B, and C of a square ABCD. The distances between the charges are determined by the geometry of the square.
Let the side length of the square be a.
- The distance between charges at A and B (i.e., F12) is equal to the side of the square: dAB=a.
- The distance between charges at A and C (i.e., F13) is the diagonal of the square: dAC=√2a.
Using Coulomb's Law, the force between two point charges is given by:
F=kq1q2r2
where k is Coulomb's constant.
F12=kq1q2d2AB=kq2a2
F13=kq1q3d2AC=kq2(√2a)2=kq22a2
Now we can find the ratio of the magnitudes of the forces:
F12F13=kq2a2kq22a2=112=2
Thus, the ratio of the magnitudes F12 and F13 is:
F12F13=2
Topper's Solved these Questions
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (ELECTRIC POTENTIAL & CAPACITANCE )
143 Videos
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (CUTTENT ELECTRICITY )
108 Videos
- ALTERNATING CURRENTBOOK - AAKASH SERIESCHAPTER - ALTERNATING CURRENTEXERCISE - EXERCISE - III
24 Videos
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - LAW OF MOTION
128 Videos
Similar Questions
Three equal charges are placed on the three corners of a square. If the force between q1 and q2 is F12 and that between q1 and q3 is F13, then the ratio of magnitudes (F12/F13) is
View SolutionFour charges of +q, +q +q and +q are placed at the corners A, B, C and D of s square. The resultant force on the charge at D
View SolutionEqual charges Q are placed at the four corners A, B, C, D of a square of length a. The magnitude of the force on the charge at B will be
View SolutionFour charges of +q, +q +q and +q are placed at the corners A, B, C and D of s square. The resultant force on the charge at D
View SolutionThree charges, each equal to q, are placed at the three. corners of a square of side a . Find the electric field at. the fourth corner.
View SolutionThree charges, each equal to q, are placed at the three. corners of a square of side a . Find the electric field at. the fourth corner.
View SolutionThree charges −q1,+q2 and −q3 are placed as shown in the figure. The x-component of the force on −q1 is proportional to
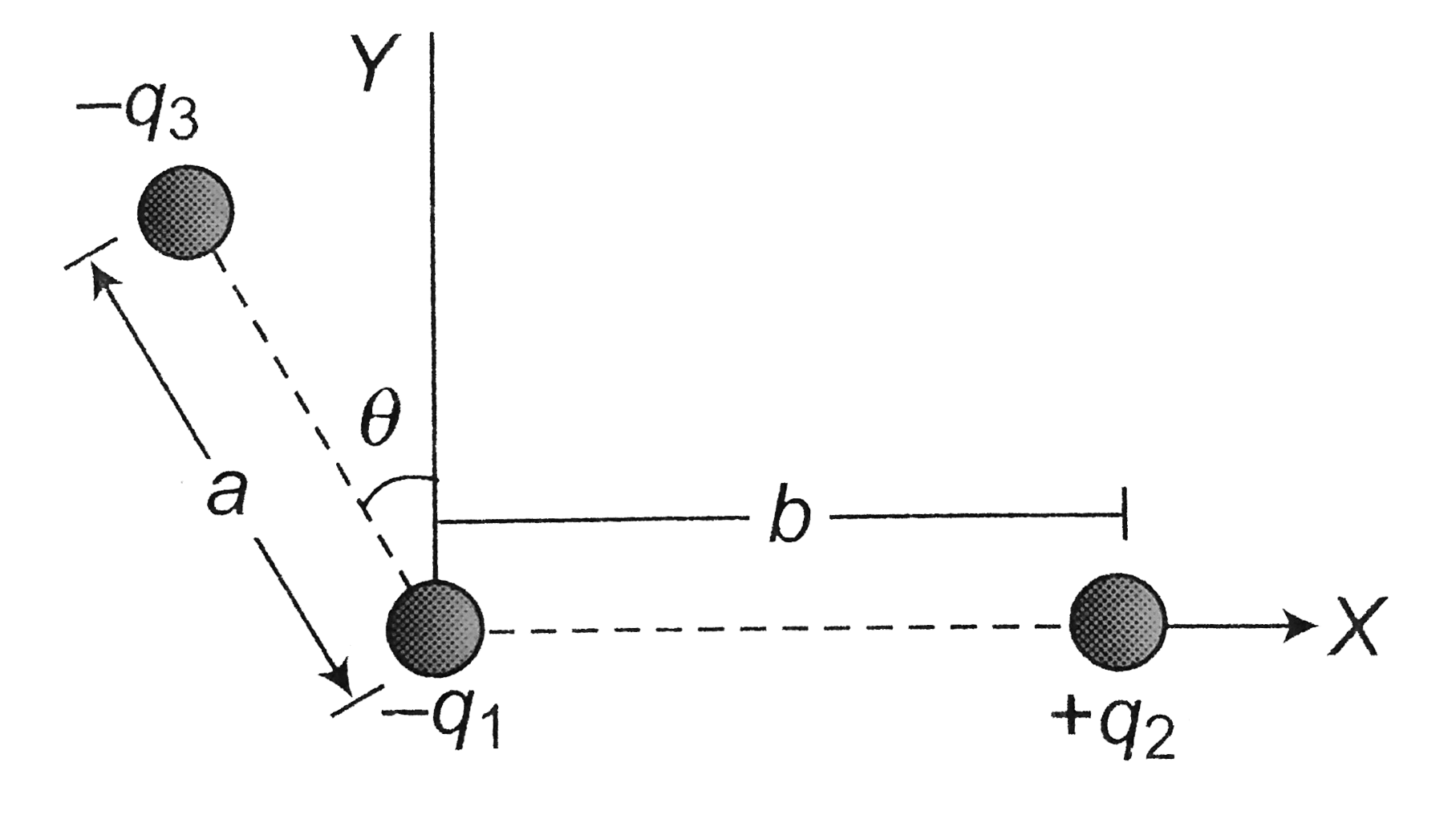
View SolutionFour charges equal to −Q are placed at the four corners of a square and a charge q is at its centre. If the system is in equilibrium the value of q is
View SolutionFour electric charges +q,+q,−q and −q are placed at the corners of a square of side 2L (see figure). The electric potential at point A, mid-way between the two charges +q and +q, is

View SolutionFour charge Q,q,Q and q are kept at the four corners of a square as shown below. What is the relation between Q and q, so that the net force on a charge q is zero ?

View Solution

