Three charges, each equal to q, are placed at the three. corners of a square of side a . Find the electric field at. the fourth corner.
To find the electric field at the fourth corner of a square due to three charges placed at the other three corners, we can follow these steps:
Step 1: Understand the Configuration
We have a square with side length a. Let's label the corners of the square as follows:
- Corner A (0, 0) has charge q
- Corner B (a, 0) has charge q
- Corner C (a, a) has charge q
- Corner D (0, a) is the corner where we want to find the electric field.
Step 2: Calculate the Electric Field Due to Each Charge at Corner D
1. Electric Field due to Charge at Corner A (E1):
- The distance from A to D is a.
- The electric field E1 due to charge q at A at point D is given by:
E1=kqa2
- The direction of E1 is upwards (along the positive y-axis).
2. Electric Field due to Charge at Corner B (E2):
- The distance from B to D is also a.
- The electric field E2 due to charge q at B at point D is given by:
E2=kqa2
- The direction of E2 is to the left (along the negative x-axis).
3. Electric Field due to Charge at Corner C (E3):
- The distance from C to D is √2a (the diagonal distance).
- The electric field E3 due to charge q at C at point D is given by:
E3=kq(a√2)2=kq2a2
- The direction of E3 is diagonally downwards towards D, which can be resolved into components.
Step 3: Resolve E3 into Components
- The components of E3:
- E3x=−kq2a2⋅1√2=−kq2√2a2 (to the left)
- E3y=−kq2a2⋅1√2=−kq2√2a2 (downwards)
Step 4: Calculate the Net Electric Field at D
- The total electric field in the x-direction:
Enet,x=E2+E3x=−kqa2−kq2√2a2
- The total electric field in the y-direction:
Enet,y=E1+E3y=kqa2−kq2√2a2
Step 5: Combine the Components
- The resultant electric field Enet can be found using the Pythagorean theorem:
Enet=√(Enet,x)2+(Enet,y)2
Step 6: Final Expression
Substituting the values from steps 4 and 5 will give us the final expression for the electric field at corner D.
We have a square with side length a. Let's label the corners of the square as follows:
- Corner A (0, 0) has charge q
- Corner B (a, 0) has charge q
- Corner C (a, a) has charge q
- Corner D (0, a) is the corner where we want to find the electric field.
1. Electric Field due to Charge at Corner A (E1):
- The distance from A to D is a.
- The electric field E1 due to charge q at A at point D is given by:
E1=kqa2
- The direction of E1 is upwards (along the positive y-axis).
- The distance from B to D is also a.
- The electric field E2 due to charge q at B at point D is given by:
E2=kqa2
- The direction of E2 is to the left (along the negative x-axis).
- The distance from C to D is √2a (the diagonal distance).
- The electric field E3 due to charge q at C at point D is given by:
E3=kq(a√2)2=kq2a2
- The direction of E3 is diagonally downwards towards D, which can be resolved into components.
- The components of E3:
- E3x=−kq2a2⋅1√2=−kq2√2a2 (to the left)
- E3y=−kq2a2⋅1√2=−kq2√2a2 (downwards)
- The total electric field in the x-direction:
Enet,x=E2+E3x=−kqa2−kq2√2a2
Enet,y=E1+E3y=kqa2−kq2√2a2
- The resultant electric field Enet can be found using the Pythagorean theorem:
Enet=√(Enet,x)2+(Enet,y)2
Substituting the values from steps 4 and 5 will give us the final expression for the electric field at corner D.
Topper's Solved these Questions
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Exercises
75 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - question for short answer
14 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Objective 2
7 Videos
- ELECTRIC CURRENT THROUGH GASESBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT THROUGH GASESEXERCISE - Short answer
6 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Questions for short answer
9 Videos
Similar Questions
Three masses, each equal to M, are placed at the three corners of a square of side a. the force of attraction on unit mass at the fourth corner will be
View SolutionFive equal charges each of value q are placed at the corners of a regular pentagon of side a. The electric field at the centre of the pentagon is
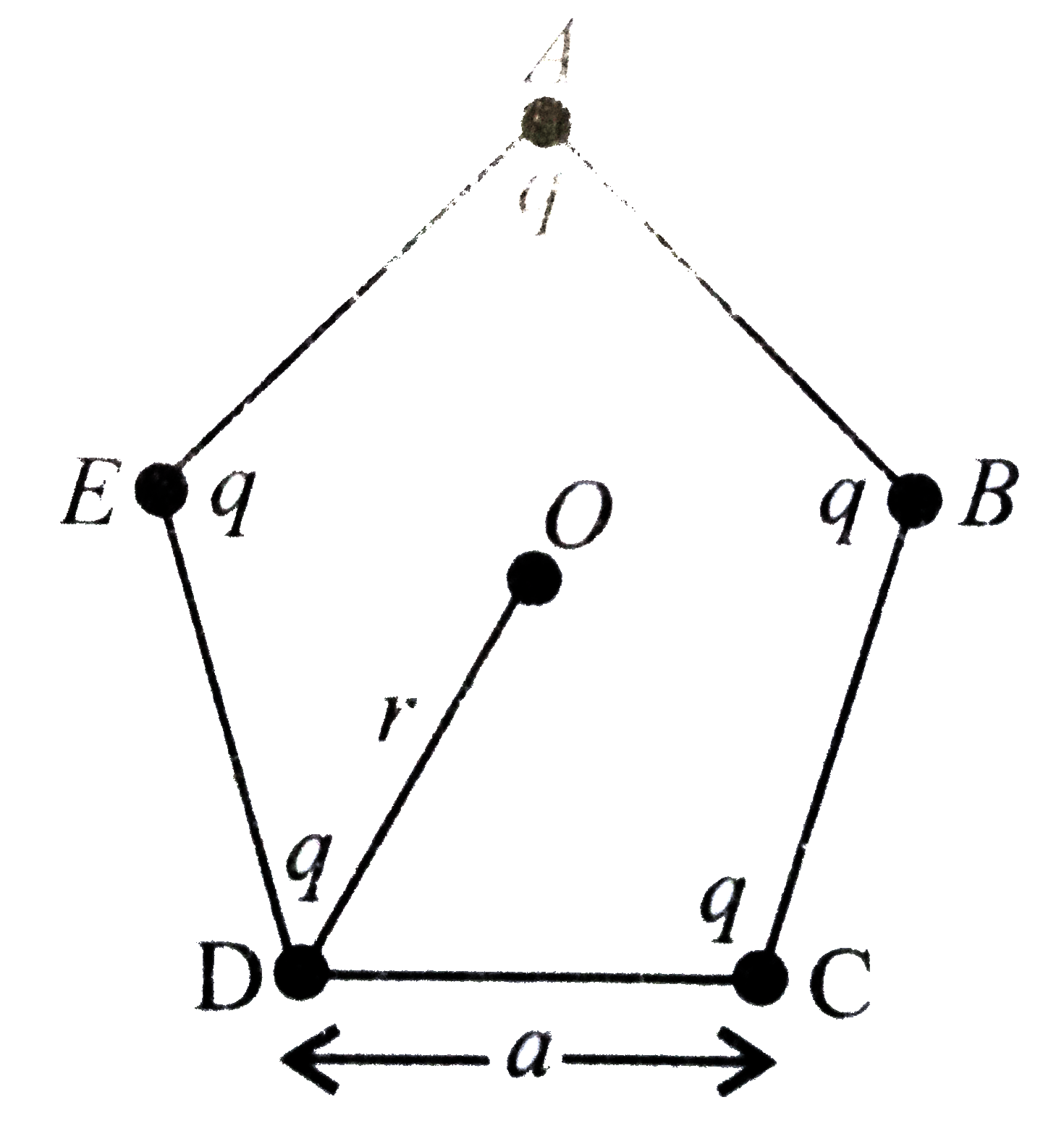
View SolutionA point charge Q is placed at the corner of a square of side a. Find the flux through the square.
View SolutionFive charges, q each are placed at the corners of a regular pentagon of side a.
(i) What will be the electric field at O if the charge from one of the corners (say A) is removed ?
(ii) What will be the electric field at O if the charge gat A is replaced by -q?
View SolutionTwo charges each equal to ηq(η−1<√3) are placed at the corners of an equilateral triangle of side a. The electric field at the third corner is E3 where(E0=q/4πε0a2)
View SolutionFive charges, q each are placed at the coreners of a regular pentagone of side.
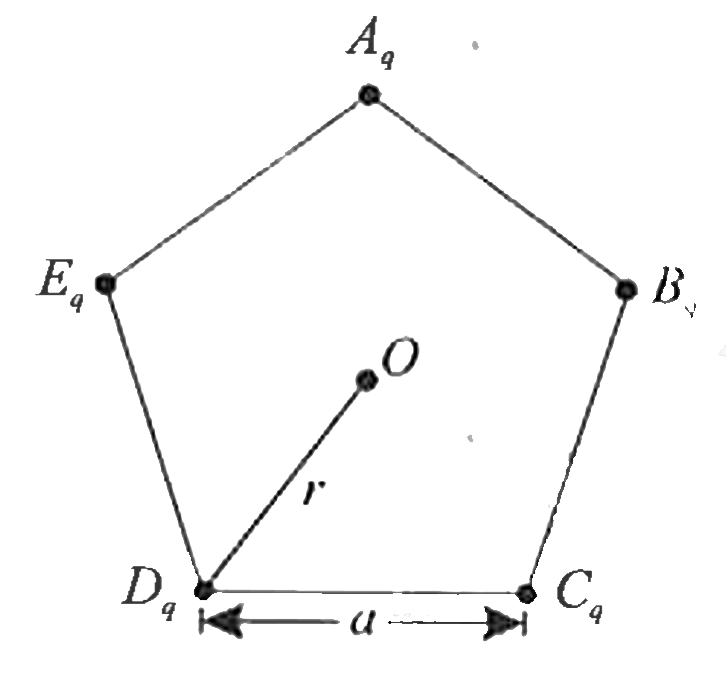
(a) (i) What will be the electric field at O, the centre of the pentagon ?
(ii) What will be the electric field 0 if the charge from one of the corners (say A) is removed ?
(iii) What will be the electric field at 0 if the charge q at A is replaced by −q ?
(b) How would your answer to (a) be affected if pentagon is replaced by n-sided regular polygon with charge q at each of its coreners ?
View SolutionFour identical charges each .q. are placed at four corners of a square of side .a.. Find the charge to be placed at the centre of the square so that the system of charges is in equilibrium
View SolutionThree particle of mas m each are placed at the three corners of an equlateral triangle of side a. Find the work which should be done on this system to increase the sides of the triangle to 2a.
View SolutionThree equal charges, each +q are placed on the corners of an equilatreal triangel . The electric field intensity at the centroid of the triangle is
View SolutionThree charges each of +4μC are the corners B, C, D of a square ABCD of side 1m. The electric field at the centre .O. of the square is
View Solution
