Four charges of +q, +q +q and +q are placed at the corners A, B, C and D of s square. The resultant force on the charge at D
q28π∈0a2(1+2√2)
2q2π∈0a2
q28π∈0a2x2√2
zero
The correct Answer is:A
To find the resultant force on the charge at point D due to the other three charges at points A, B, and C, we can follow these steps:
Step 1: Identify the Charges and Their Positions
We have four charges of +q placed at the corners of a square ABCD. The positions of the charges are:
- Charge at A: +q
- Charge at B: +q
- Charge at C: +q
- Charge at D: +q (the charge we are analyzing)
Step 2: Calculate the Forces Acting on Charge D
The forces acting on charge D due to the other charges can be calculated using Coulomb's Law, which states that the force between two charges is given by:
F=14πϵ0q1q2r2
Force on D due to A (F_AD):
The distance from A to D is equal to the side of the square (a):
FAD=14πϵ0q2a2
Force on D due to B (F_BD):
The distance from B to D is also equal to the side of the square (a):
FBD=14πϵ0q2a2
Force on D due to C (F_CD):
The distance from C to D is equal to the diagonal of the square, which is √2a:
FCD=14πϵ0q2(√2a)2=14πϵ0q22a2
Step 3: Determine the Directions of the Forces
- The force FAD acts directly towards A (to the left).
- The force FBD acts directly towards B (upwards).
- The force FCD acts directly towards C (diagonally downwards).
Step 4: Resolve Forces into Components
Since FAD and FBD are perpendicular to each other, we can use the Pythagorean theorem to find the resultant of these two forces.
Let:
- FAD=F1=14πϵ0q2a2
- FBD=F2=14πϵ0q2a2
The resultant force FAB from A and B is:
FAB=√F21+F22=√(14πϵ0q2a2)2+(14πϵ0q2a2)2
=√2(14πϵ0q2a2)2
=14πϵ0q2a2√2
Step 5: Add the Force from C
Now, we need to add the force from C, which is acting diagonally towards D:
FCD=14πϵ0q22a2
Step 6: Calculate the Total Resultant Force on D
The total force Fnet on charge D is the vector sum of FAB and FCD:
Fnet=FAB+FCD
Substituting the values:
Fnet=14πϵ0q2a2√2+14πϵ0q22a2
Factoring out 14πϵ0q2a2:
Fnet=14πϵ0q2a2(√2+12)
Final Result
Thus, the resultant force on the charge at D is:
Fnet=14πϵ0q2a2(12+√2)
We have four charges of +q placed at the corners of a square ABCD. The positions of the charges are:
- Charge at A: +q
- Charge at B: +q
- Charge at C: +q
- Charge at D: +q (the charge we are analyzing)
The forces acting on charge D due to the other charges can be calculated using Coulomb's Law, which states that the force between two charges is given by:
The distance from A to D is equal to the side of the square (a):
FAD=14πϵ0q2a2
The distance from B to D is also equal to the side of the square (a):
FBD=14πϵ0q2a2
The distance from C to D is equal to the diagonal of the square, which is √2a:
FCD=14πϵ0q2(√2a)2=14πϵ0q22a2
- The force FAD acts directly towards A (to the left).
- The force FBD acts directly towards B (upwards).
- The force FCD acts directly towards C (diagonally downwards).
Since FAD and FBD are perpendicular to each other, we can use the Pythagorean theorem to find the resultant of these two forces.
- FAD=F1=14πϵ0q2a2
- FBD=F2=14πϵ0q2a2
FAB=√F21+F22=√(14πϵ0q2a2)2+(14πϵ0q2a2)2
=√2(14πϵ0q2a2)2
=14πϵ0q2a2√2
Now, we need to add the force from C, which is acting diagonally towards D:
FCD=14πϵ0q22a2
The total force Fnet on charge D is the vector sum of FAB and FCD:
Fnet=FAB+FCD
Substituting the values:
Fnet=14πϵ0q2a2√2+14πϵ0q22a2
Factoring out 14πϵ0q2a2:
Fnet=14πϵ0q2a2(√2+12)
Thus, the resultant force on the charge at D is:
Fnet=14πϵ0q2a2(12+√2)
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDSBOOK - AAKASH SERIESCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Exercise
57 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - AAKASH SERIESCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Exercise-I
80 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - AAKASH SERIESCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - PRACTICE EXERCISEX
42 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - AAKASH SERIESCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - PROBLEMS (LEVEL-II)
26 Videos
Similar Questions
Four charges of +q, +q +q and +q are placed at the corners A, B, C and D of s square. The resultant force on the charge at D
View SolutionEqual charges Q are placed at the four corners A, B, C, D of a square of length a. The magnitude of the force on the charge at B will be
View SolutionFour point charge q,−q,2Q and Q are placed in order at the corners A, B, C and D of a square. If the field at the midpoint of CD is zero then the value of q/Q is 5√5x. Find the value of x.
View SolutionFour charges +q,+q,−q,and−q are placed, respectively, at the corners A,B,C,andD of a square of side a, arranged in the given order. EandF are the midpoints of sides BCandCD, respectively, O is the center of square.
The work done in carrying a charge e from O to F is.
View SolutionFour charges +q,+q,−q,and−q are placed, respectively, at the corners A,B,C,andD of a square of side a, arranged in the given order. EandF are the midpoints of sides BCandCD, respectively, O is the center of square.
The work done in carrying a charge e from O to E is.
View SolutionFour charges +q,+q,−q,and−q are placed, respectively, at the corners A,B,C,andD of a square of side a, arranged in the given order. EandF are the midpoints of sides BCandCD, respectively, O is the center of square.
The electric potential at O is.
View SolutionFour charges +q,+q,−q,and−q are placed, respectively, at the corners A,B,C,andD of a square of side a, arranged in the given order. If O is the center of square.
The electric field at O is.
View SolutionCharges q,2q,3q and 4q are placed at the corners A,B,C and D of a square as shown in the following figure. The directon of electric field at the centre of the square is along

View SolutionCharges q,2q,3q and 4q are placed at the corners A,B,C and D of a square as shown in the following figure. The directon of electric field at the centre of the square is along

View SolutionThree charges of (+2q),(−q) and (−q) are placed at the corners A,B and C of an equilateral triangle of side a as shown in the adjoining figure. Then the dipole moment of this combination is
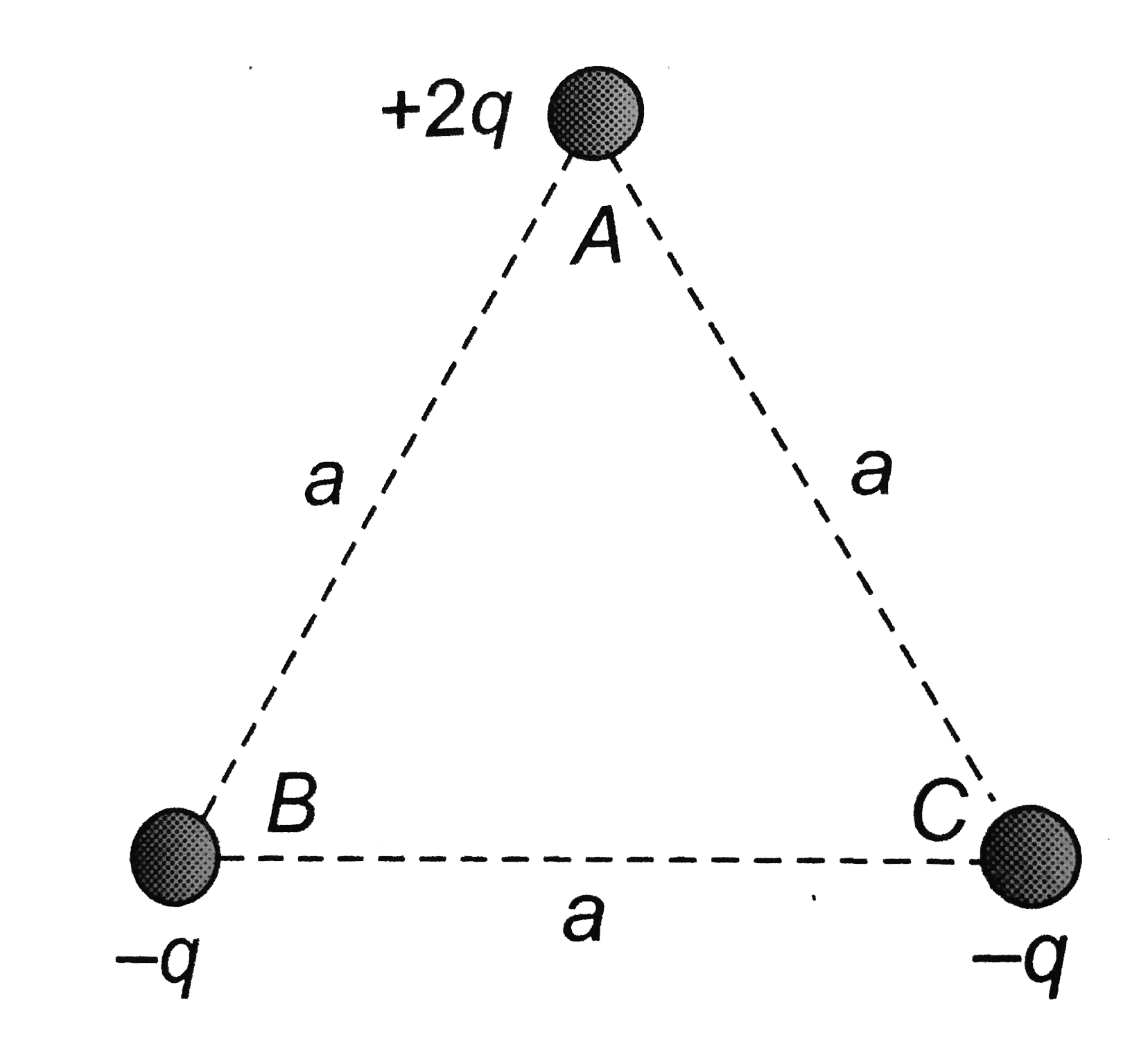
View Solution
