Four charges +q,+q,−q,and−q are placed, respectively, at the corners A,B,C,andD of a square of side a, arranged in the given order. EandF are the midpoints of sides BCandCD, respectively, O is the center of square.
The electric potential at O is.
√2qπε0a
√3qπε0a
qπε0a
zero
The correct Answer is:D
To find the electric potential at the center O of the square formed by the charges +q,+q,−q,−q at the corners A,B,C,D respectively, we can follow these steps:
Step 1: Understand the Configuration
We have a square with side length a. The charges are placed at the corners:
- Charge at A (top left) = +q
- Charge at B (top right) = +q
- Charge at C (bottom right) = −q
- Charge at D (bottom left) = −q
The center O of the square is equidistant from all four corners.
Step 2: Calculate the Distance from Center to Corners
The distance from the center O to any corner (say A) can be calculated using the Pythagorean theorem:
OA=√(a2)2+(a2)2=√a24+a24=√a22=a√2
Thus, the distance OA=OB=OC=OD=a√2.
Step 3: Use the Formula for Electric Potential
The electric potential V due to a point charge Q at a distance R is given by:
V=14πϵ0QR
Step 4: Calculate the Electric Potential at Point O
The total electric potential at point O due to all four charges is the sum of the potentials due to each charge:
VO=VA+VB+VC+VD
Calculating each term:
- VA=14πϵ0+qa√2=q√24πϵ0a
- VB=14πϵ0+qa√2=q√24πϵ0a
- VC=14πϵ0−qa√2=−q√24πϵ0a
- VD=14πϵ0−qa√2=−q√24πϵ0a
Step 5: Combine the Potentials
Now, we can combine these potentials:
VO=(q√24πϵ0a+q√24πϵ0a−q√24πϵ0a−q√24πϵ0a)
This simplifies to:
VO=0
Conclusion
The electric potential at the center O of the square is 0.
---
We have a square with side length a. The charges are placed at the corners:
- Charge at A (top left) = +q
- Charge at B (top right) = +q
- Charge at C (bottom right) = −q
- Charge at D (bottom left) = −q
The distance from the center O to any corner (say A) can be calculated using the Pythagorean theorem:
OA=√(a2)2+(a2)2=√a24+a24=√a22=a√2
Thus, the distance OA=OB=OC=OD=a√2.
The electric potential V due to a point charge Q at a distance R is given by:
V=14πϵ0QR
The total electric potential at point O due to all four charges is the sum of the potentials due to each charge:
VO=VA+VB+VC+VD
- VA=14πϵ0+qa√2=q√24πϵ0a
- VB=14πϵ0+qa√2=q√24πϵ0a
- VC=14πϵ0−qa√2=−q√24πϵ0a
- VD=14πϵ0−qa√2=−q√24πϵ0a
Now, we can combine these potentials:
VO=(q√24πϵ0a+q√24πϵ0a−q√24πϵ0a−q√24πϵ0a)
This simplifies to:
VO=0
The electric potential at the center O of the square is 0.
Topper's Solved these Questions
- ELECTRIC POTENTIALBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRIC POTENTIALExercise:Integer
Explore 5 Videos
- ELECTRIC POTENTIALBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRIC POTENTIALExercise:DPP 3.1
Explore 14 Videos
- ELECTRIC POTENTIALBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRIC POTENTIALExercise:Multiple Correct
Explore 10 Videos
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRIC FLUX AND GAUSS LAWExercise:MCQ s
Explore 38 Videos
- ELECTRICAL MEASURING INSTRUMENTSBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRICAL MEASURING INSTRUMENTSExercise:M.C.Q
Explore 2 Videos
Similar Questions
Four charges +q,+q,−q,and−q are placed, respectively, at the corners A,B,C,andD of a square of side a, arranged in the given order. If O is the center of square.
The electric field at O is.
View SolutionFour charges +q,+q,−q,and−q are placed, respectively, at the corners A,B,C,andD of a square of side a, arranged in the given order. EandF are the midpoints of sides BCandCD, respectively, O is the center of square.
The work done in carrying a charge e from O to F is.
View SolutionFour charges +q,+q,−q,and−q are placed, respectively, at the corners A,B,C,andD of a square of side a, arranged in the given order. EandF are the midpoints of sides BCandCD, respectively, O is the center of square.
The work done in carrying a charge e from O to E is.
View SolutionFour charges of +q, +q +q and +q are placed at the corners A, B, C and D of s square. The resultant force on the charge at D
View SolutionFour charges of +q, +q +q and +q are placed at the corners A, B, C and D of s square. The resultant force on the charge at D
View SolutionCharges q,2q,3q and 4q are placed at the corners A,B,C and D of a square as shown in the following figure. The directon of electric field at the centre of the square is along
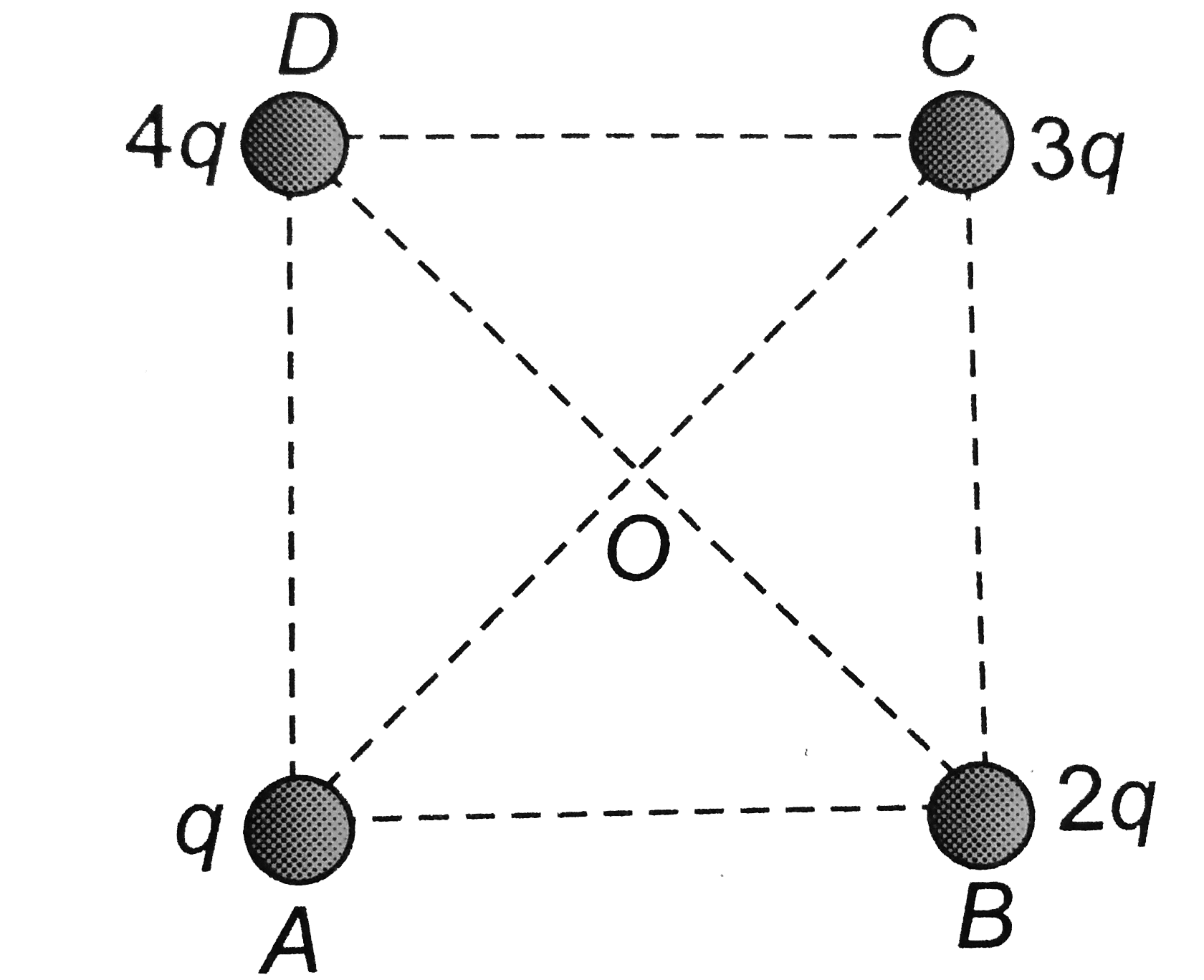
View SolutionCharges q,2q,3q and 4q are placed at the corners A,B,C and D of a square as shown in the following figure. The directon of electric field at the centre of the square is along

View SolutionThree charges of (+2q),(−q) and (−q) are placed at the corners A,B and C of an equilateral triangle of side a as shown in the adjoining figure. Then the dipole moment of this combination is
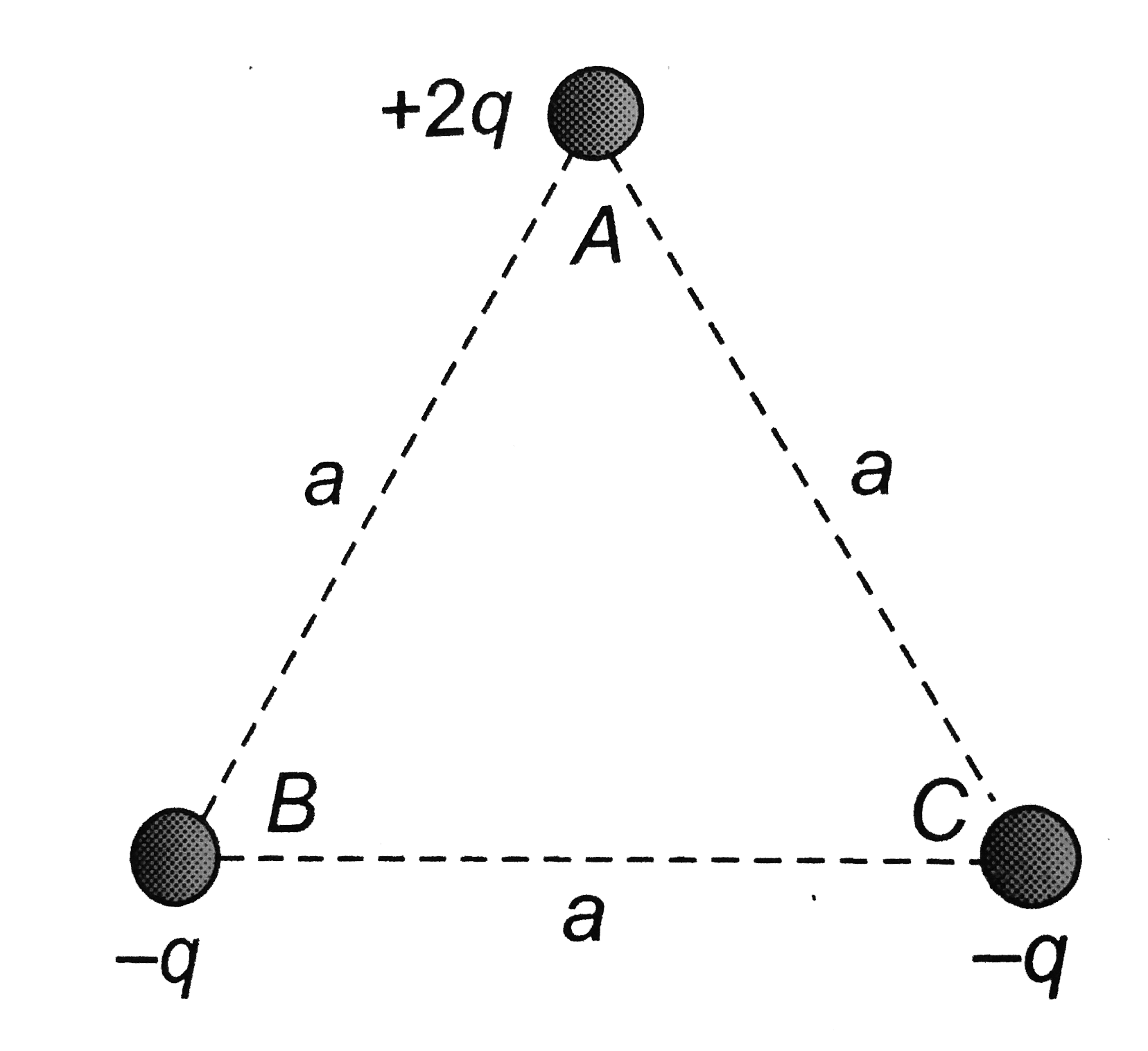
View SolutionFour point charges are respectively placed at the corners A, B, C and D of a square of side a. If F is the mid-point of side CD, the work done in carrying an electron of charge from O [the centre of the square] to F fill be:
View SolutionEqual charges Q are placed at the four corners A, B, C, D of a square of length a. The magnitude of the force on the charge at B will be
View Solution