In a regular hexagon each corner is at a distance .r. from the centre. Identical charges of magnitude .Q. are placed at 5 corners. The field at the centre is (K=14π∈0)
KQ/r2
6KQr2
5KQr2
zero
The correct Answer is:A
To find the electric field at the center of a regular hexagon with identical charges placed at five of its corners, we can follow these steps:
Step 1: Understand the Configuration
In a regular hexagon, all corners are equidistant from the center. Let’s denote the distance from the center to each corner as r. We have identical charges Q placed at five corners of the hexagon.
Step 2: Determine the Electric Field Contribution
The electric field E due to a point charge Q at a distance r is given by the formula:
E=kQr2
where k=14πϵ0.
Step 3: Analyze the Directions of the Electric Fields
Since there are five charges, we need to consider the direction of the electric field produced by each charge at the center:
- The electric field due to each charge will point away from the charge (since they are positive charges).
- The symmetry of the hexagon means that some of these electric fields will cancel each other out.
Step 4: Identify Canceling Pairs
- The electric fields from charges at opposite corners will cancel each other.
- For example, if we label the corners as 1, 2, 3, 4, 5, and 6 (where corner 6 has no charge), the pairs (1, 4) and (2, 5) will cancel each other out.
Step 5: Calculate the Resultant Electric Field
The only charge that does not have a canceling counterpart is the charge at corner 3. The electric field due to this charge at the center will be:
E3=kQr2
This is the only contribution to the electric field at the center since the other fields cancel out.
Step 6: Final Result
Thus, the total electric field at the center of the hexagon is simply:
Etotal=E3=kQr2
Summary
The electric field at the center of the hexagon, with charges at five corners, is given by:
E=kQr2
In a regular hexagon, all corners are equidistant from the center. Let’s denote the distance from the center to each corner as r. We have identical charges Q placed at five corners of the hexagon.
The electric field E due to a point charge Q at a distance r is given by the formula:
E=kQr2
where k=14πϵ0.
Since there are five charges, we need to consider the direction of the electric field produced by each charge at the center:
- The electric field due to each charge will point away from the charge (since they are positive charges).
- The symmetry of the hexagon means that some of these electric fields will cancel each other out.
- The electric fields from charges at opposite corners will cancel each other.
- For example, if we label the corners as 1, 2, 3, 4, 5, and 6 (where corner 6 has no charge), the pairs (1, 4) and (2, 5) will cancel each other out.
The only charge that does not have a canceling counterpart is the charge at corner 3. The electric field due to this charge at the center will be:
E3=kQr2
This is the only contribution to the electric field at the center since the other fields cancel out.
Thus, the total electric field at the center of the hexagon is simply:
Etotal=E3=kQr2
The electric field at the center of the hexagon, with charges at five corners, is given by:
E=kQr2
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDSBook:AAKASH SERIESChapter:ELECTRIC CHARGES AND FIELDSExercise:Practice Exercise
Explore 57 Videos
- ELECTRIC CHARGES AND FIELDSBook:AAKASH SERIESChapter:ELECTRIC CHARGES AND FIELDSExercise:Exercise-I
Explore 80 Videos
- DUAL NATURE OF RADIATION AND MATTERBook:AAKASH SERIESChapter:DUAL NATURE OF RADIATION AND MATTERExercise:PRACTICE EXERCISEX
Explore 42 Videos
- ELECTRIC FIELD AND POTENTIALBook:AAKASH SERIESChapter:ELECTRIC FIELD AND POTENTIALExercise:PROBLEMS (LEVEL-II)
Explore 26 Videos
Similar Questions
In a regular polygon of n sides, each corner is at a distance r from the centre. Identical charges each of magnitude q are placed at corners. The field at the centre is
View SolutionIn a regular polygon of n sides, each corner is at a distance r from the centre. Identical charges are placed at (n−1) corners. At the centre, the intensity is E and the potential is V. The ratio V/E has magnitude
View Solution
Knowledge Check
In a regular polygon of n sides, each corner is at a distance r from the centre. Identical charges are placed at (n−1) corners. At the centre, the intensity is E and the potential is V. The ratio V/E has magnitude
ArnBr(n−1)C(n−1)/rDr(n−1)/n
ABC is an equilateral triangle. Charges +q are placed at each corner. The electric field intensity at the centroid of triangle will be
View SolutionA charge Q is placed at each corner of a cube of side a. The potential at the centre of the cube is
View SolutionA regular hexagon of side a has a charge Q at each vertex. Potential at the centres of hexagon is (k= (14πε0))
View SolutionInside a neutral hollow conducting sphere of radius X and centre C, a point charge q is placed as shown in the figure. Another point charge q1, is placed outside the sphere at distance d from centre. The net- electrostatic force on charge q placed at the centre is K=14πε0
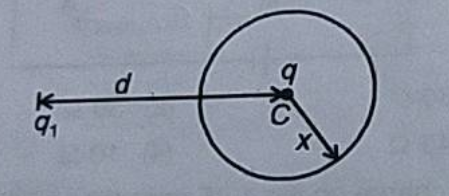
View SolutionFive charges each q are placed at five corners regular pentagon. Distance from corner to the centre of pontagon is r. Then (K=14πε0)
View SolutionABC is an equilateral triangle. Charges +q are placed at each corner. The electric field intensity at the centroid of triangle will be
View SolutionLet a total charge 2Q be distributed in a sphere of radius R, with the charge density given by , ρ(r)=kr, where r is the distance from the centre. Two charge A and B, of –Q each, are placed on diametrically opposite points, at equal distance, a from the centre. If A and B do not experience any force, then:
View Solution

