A charge Q is placed at each corner of a cube of side a. The potential at the centre of the cube is
8Qπ∈aa
4Q4π∈0a
4Q√3π∈0a
4Qπ∈aa
The correct Answer is:C
To find the potential at the center of a cube with charge Q placed at each corner, we can follow these steps:
Step 1: Understand the Geometry of the Cube
The cube has a side length a. Each corner of the cube has a charge Q. The center of the cube is equidistant from all corners.
Step 2: Calculate the Distance from a Corner to the Center
The distance R from a corner of the cube to the center can be found using the body diagonal of the cube. The length of the body diagonal d of a cube with side a is given by:
d=√a2+a2+a2=√3a2=a√3
Since the center is at half the length of the body diagonal, the distance R is:
R=d2=a√32
Step 3: Use the Formula for Electric Potential
The electric potential V due to a point charge Q at a distance R is given by:
V=kQR
where k=14πϵ0.
Step 4: Calculate the Total Potential at the Center
Since there are 8 charges at the corners of the cube, the total potential Vnet at the center is the sum of the potentials due to each charge:
Vnet=8×kQR
Step 5: Substitute the Expression for R
Substituting R=a√32 into the equation gives:
Vnet=8×kQa√32=8×k2Qa√3=16kQa√3
Step 6: Substitute the Value of k
Now substituting k=14πϵ0:
Vnet=16⋅14πϵ0Qa√3=4Qπϵ0a√3
Final Answer
Thus, the potential at the center of the cube is:
Vnet=4Qπϵ0a√3
The cube has a side length a. Each corner of the cube has a charge Q. The center of the cube is equidistant from all corners.
The distance R from a corner of the cube to the center can be found using the body diagonal of the cube. The length of the body diagonal d of a cube with side a is given by:
d=√a2+a2+a2=√3a2=a√3
Since the center is at half the length of the body diagonal, the distance R is:
R=d2=a√32
The electric potential V due to a point charge Q at a distance R is given by:
V=kQR
where k=14πϵ0.
Since there are 8 charges at the corners of the cube, the total potential Vnet at the center is the sum of the potentials due to each charge:
Vnet=8×kQR
Substituting R=a√32 into the equation gives:
Vnet=8×kQa√32=8×k2Qa√3=16kQa√3
Now substituting k=14πϵ0:
Vnet=16⋅14πϵ0Qa√3=4Qπϵ0a√3
Thus, the potential at the center of the cube is:
Vnet=4Qπϵ0a√3
Topper's Solved these Questions
- ELECTROSTATICSBook:AAKASH SERIESChapter:ELECTROSTATICSExercise:PRACTICE SHEET (EXERCISE -IV ELECTRIC POTENTIAL & POTENTIAL ENERGY) (LEVEL - II (ADVANCED) MORE THAN ONE CORRECT ANSWER TYPE QUESTION)
Explore 1 Video
- ELECTROSTATICSBook:AAKASH SERIESChapter:ELECTROSTATICSExercise:PRACTICE SHEET (EXERCISE -IV ELECTRIC POTENTIAL & POTENTIAL ENERGY) (LEVEL - II (ADVANCED) LINKED COMPREHENSION TYPE QUESTION)
Explore 2 Videos
- ELECTROSTATICSBook:AAKASH SERIESChapter:ELECTROSTATICSExercise:PRACTICE SHEET (EXERCISE -IV ELECTRIC POTENTIAL & POTENTIAL ENERGY) (LEVEL - I (MAIN) STRAIGHT OBJECTIVE TYPE QUESTION)
Explore 19 Videos
- ELECTROMAGNETICSBook:AAKASH SERIESChapter:ELECTROMAGNETICSExercise:ADDITIONAL EXERCISE
Explore 13 Videos
- ELEMENTS OF VECTORSBook:AAKASH SERIESChapter:ELEMENTS OF VECTORSExercise:QUESTIONS FOR DESCRIPTIVE ANSWERS
Explore 10 Videos
Similar Questions
Electric charges of +10μC,+5μC,−3μCand+8μC are placed at the corners of a square of side √2 m, the potential at the centre of the square is
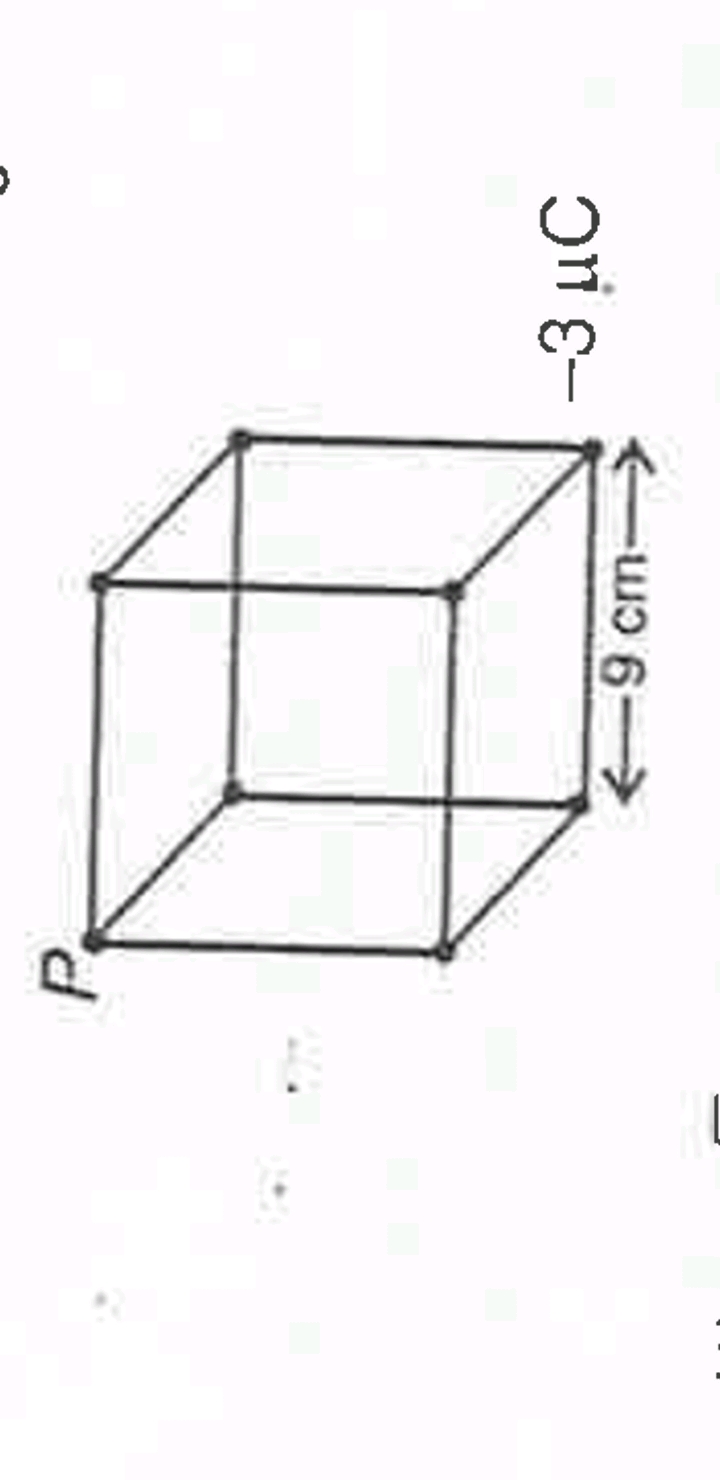
View SolutionA charge -3 μC is placed at one corner of cube of side 9 cm . The potential at a point P which diagonally opposite as shown in fugure is
View SolutionFour point charges are placed at the corners of a square of side l. Calculate potential at the centre of square.

View SolutionFour identical charges q are placed at the corners of a square of side a. Find the potential energy of one of the charges due to the remaining charges.
 .
.
View SolutionFour identical point charges q are placed at four corners of a square of side a. Find the potential energy of the charge system.
 .
.
View SolutionIf identical charges (−q) are placed at each corner of a cube of side b, then electric potential energy of charge (+q) which is placed at centre of the cube will be
View SolutionEight equal point charges are placed at corners of a cube side length a. The potential and electric field magnitude at the centre of cube will be
View SolutionA charge Q is placed at the corner of a cube of edge length L. The electric flux linked to one of the faces not touching the charge Q is
View SolutionA charge +q is placed at the mid point of a cube of side L. The electric flux emerging from cube is
View SolutionFive equal charges each of value q are placed at the corners of a regular pentagon of side a. The electric field at the centre of the pentagon is

View Solution

